使用Pytorch实现简单线性回归

我们的任务是给定一些数据点，这些数据点为一次函数加噪声构成。我们需要通过训练得出一次函数的各个参数。
数据的公式表达为
$$y=wx+b+c$$
其中，y是最终的数据，w和b是我们需要求的参数，c是噪声。

第一步：生成数据集

我们随机一个x的列表，使用一个真实的w和b去计算它对应的y的值，再给y的值加上一个噪声，并将噪声后的数据作为我们的训练数据。

%matplotlib inline   
#此语句可以让plot绘制的图直接显示在jupyter 的控制台里
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random

num_inputs = 2
num_examples = 1000
true_w = [2,-3.4]
true_b = 3.2
features = torch.from_numpy(np.random.normal(0,1,(num_examples,num_inputs)))
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b  #生成正确的数据,这里是y

#给正确的数据加一点噪声
labels += torch.from_numpy(np.random.normal(0,0.01,size = labels.size()))  #np.random.normal参数：均值  标准差  输出的矩阵大小

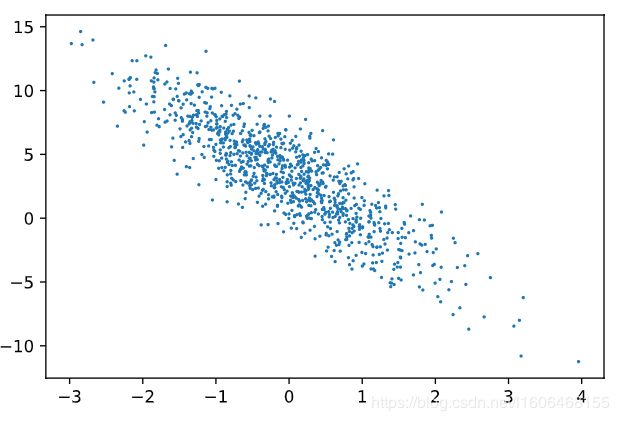
plt.scatter(features[:,1].numpy(),labels.numpy(),1);

我们这里生成了1000个值，并绘制它的图形如下：

定义数据读取函数

接下来我们来定义一个数据读取的函数，作用是每次随机从我们生成的数据集了读取一个batch的数据

#数据读取函数，每次从features和labels中随机读取一个批次的数据
def data_iter(batch_size,features,labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  #随机排列样本
    for i in range(0,num_examples,batch_size):
        j = torch.LongTensor(indices[i:min(i + batch_size,num_examples)])   #将下标切片，并转换成LongTensor类型赋给j
        
        yield features.index_select(0,j),labels.index_select(0,j)

初始化模型参数

这里原书上的设置的类型是torch.float32，不过前面生成的数据均为torch.float64的，在后面做矩阵乘法会因为类型不一致报错，这里修改为torch.float64

w = torch.tensor(np.random.normal(0,0.01,(num_inputs,1)),dtype = torch.float64)
b = torch.zeros(1,dtype = torch.float64)
# w.requires_grad = True
# b.requires_grad = False
#上面直接设置或者使用原地处理方式
w.requires_grad_(requires_grad = True)
b.requires_grad_(requires_grad = True)

定义模型

这里实际上就是定义了一个计算函数，计算w和b取某个值时得到的$y_1$是多少，方便后面用来计算与真实值的误差。

def linreg(x,w,b):#这里使用的torch.mm  需要保证x w 和 b类型一致   比如均为torch.float32 或者 均为 torch.float64，如果不一致会报错
    return torch.mm(x,w) + b  # 这里返回的是x与w相乘再加b  实际上即计算y

定义损失函数和优化方法

def squared_loss(y_hat,y):
    return (y_hat - y.view(y_hat.size())) ** 2 / 2    #   a**b 即a的b次方，除2应该是为了后面求导消参数 

#随机梯度下降法
def sgd(params,lr,batch_size):
    for param in params:
        param.data -= lr * param.grad / batch_size   #让其沿着梯度减少

开始训练模型

实际上就是用w和b代进去算$y_1$，然后计算损失（$y_1与y的距离$），用优化函数去降低这个损失

lr = 0.03   #学习率
num_epochs = 3 #训练次数
net = linreg #设置网络的操作，也就是前面说的那个计算y值的函数
loss = squared_loss #设置计算损失的方法
for epoch in range(num_epochs):
    for x,y in data_iter(batch_size,features,labels):
        l = loss(net(x,w,b),y).sum()  
        l.backward()
        sgd([w,b],lr,batch_size)#使用优化算法迭代模型参数
        
        #清空梯度
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features,w,b),labels)
    print('Epoch %d,loss %f ' %(epoch+1,train_l.mean().item()))

这是我这里的输出结果：

Epoch 1,loss 0.030724 
Epoch 2,loss 0.000125 
Epoch 3,loss 0.000049 

我们来比较一下真实的值和训练的值：

print(true_w,'\n',w)
print(true_b,'\n',b)

结果为：

[2, -3.4] 
 tensor([[ 1.9998],
        [-3.3995]], dtype=torch.float64, requires_grad=True)
3.2 
 tensor([3.1997], dtype=torch.float64, requires_grad=True)

我们真实的w设置的是2和-3.4，而训练得出的是1.9998和-3.3995
真实的b设置的为3.2，而训练得到的b为3.1997
可以看到，我们只训练了三次，而得到的值基本是符合趋势的，不过这只是一个很简单的模型，仅仅有两个参数，当我们模型很复杂时，我们就需要添加更多的层来训练了。

PS.

以上代码来源于Github《动手学深度学习》Pytorch版