EM算法初探——公式推导和三硬币模型解析
EM算法初探——公式推导和三硬币模型解析
转载借鉴:http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html#!comments
这篇博客是在学习了诸多网友后略有所触后记下,大部分内容还是从他们的博客中搬运,诸如推导等,在此基础上增加自己在这个过程的一些理解和注解,希望对大家有帮助,若文中有问题也希望大家指出,共同探讨学习。
- EM算法推导
- 三硬币模型解析
EM算法推导
Jensen不等式
Jensen不等式,又称琴生不等式,琴生不等式以丹麦技术大学数学家约翰·延森(Johan Jensen)命名。它给出积分的凸函数值和函数的积分值间的关系。
凸函数convex function:
对于一个函数 f(x) f ( x ) ,如果它在一个区间[a,b]中是凸函数,那么对于区间[a,b]中的任意两个点 x1 x 1 和 x2 x 2 ,对于任意的满足 0<λ<1 0 < λ < 1 的 λ λ ,均有 f[λx1+(1−λ)x2]≤λf(x1)+(1−λ)f(x2) f [ λ x 1 + ( 1 − λ ) x 2 ] ≤ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 )
凹函数concave function:
对于一个函数 f(x) f ( x ) ,如果它在一个区间[a,b]中是凹函数,那么对于区间[a,b]中的任意两个点 x1 x 1 和 x2 x 2 ,对于任意的满足 0<λ<1 0 < λ < 1 的 λ λ ,均有 f[λx1+(1−λ)x2]≥λf(x1)+(1−λ)f(x2) f [ λ x 1 + ( 1 − λ ) x 2 ] ≥ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 )
Jensen不等式表述如下:如果f是凸函数,x是随机变量,那么: E[f(x)]≥f(E(x)) E [ f ( x ) ] ≥ f ( E ( x ) ) ;如果f是凹函数,那么: E[f(x)]≥f(E(x)) E [ f ( x ) ] ≥ f ( E ( x ) ) 。
大家可以回忆一下概率中学过的期望,其实就能理解了,上面的 λ λ 定义在[0,1]区间里其实就可以理解成是概率,那最后满足凸函数的条件 f[λx1+(1−λ)x2] f [ λ x 1 + ( 1 − λ ) x 2 ] 就是把x看成是变量,求了一遍 f(E(x)) f ( E ( x ) ) ,而另外一部分的 λf(x1)+(1−λ)f(x2) λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) 就是把f(x)看作变量,最后求了关于f(x)的期望 E(f(x)) E ( f ( x ) ) 。其实就是相当于把凸函数和凹函数的定义用概率的方式再写了一遍。
这里需要注意的是等式的成立条件当且仅当函数的变量是一个常数。
EM公式的推导
假设给定的训练样本是 x(1),⋯,x(m) x ( 1 ) , ⋯ , x ( m ) ,即有m个样本,样本符合iid(独立同分布),记隐变量为z,参数为 θ θ ,使用极大似然法进行估计样本发生的概率,希望能够找到能够最大化样本发生概率的参数 θ θ :
这里做下解释,第一步是极大似然的表示方式,在独立同分布的前提下,发生当前样本集的概率便是各个样本发生的概率的连乘,这里前方加的log出于两个考虑(1)log不影响求最大值的结果,首先原先函数的域是在log函数区间内的,然后log函数满足:若 x1>x2 x 1 > x 2 ,则 log(x1)>log(x2) l o g ( x 1 ) > l o g ( x 2 ) ;(2) log(x1∗x2)=log(x1)+log(x2) l o g ( x 1 ∗ x 2 ) = l o g ( x 1 ) + l o g ( x 2 ) ,这个性质对于解开连乘提供了便利,也可以防止下界溢出。第二步便是利用log的性质将连乘解开,第三步是引入隐变量z展开z和x联合概率分布。正常的极大似然函数到了这里就会想通过求导来进行求解了,但遗憾的是log函数中还有着一个求和函数。后面数学家就用了另一个想法绕开了这个弯,迭代求解了这个极大似然函数。
这里先做一个区分,p(x,z; θ θ )是表示参数为 θ θ 时x和z的联合概率分布,因为EM算法往往都是针对估计未知变量和未知参数,有时候指定概率是需要先强调参数,比如说这里的参数是代表z是高斯分布,需要先指定这个高斯分布的均值和方差,同理p(x|z; θ θ )则代表条件概率分布。
再下一步就是一个很巧妙的证明了,通过为隐变量z假设一个分布 Qi Q i ,该分布满足 ∑zQi(z(i))=1,Qi(z(i))≥0 ∑ z Q i ( z ( i ) ) = 1 , Q i ( z ( i ) ) ≥ 0 ,借此来进行变换最后借助琴生不等式来推导出一个下界,还是很感慨数学家们的推导和创造力的。
先对里面的一些符号做些解释, z(i) z ( i ) 是联合概率分布中对样本i当前遍历到的隐变量, Qi(z(i)) Q i ( z ( i ) ) 是说对于样本i的隐变量为 z(i) z ( i ) 的概率,这可能不太好理解,其实我一开始也不理解,但你可以先看作这个概率是同时受样本和隐变量z影响的,后面再往下看就有相应的解释了。
然后继续对公式进行解释,首先式3是将第一段的推导的结果进行延续,然后在这个基础上引进了上面假设好的隐变量z的分布, Qi(zi) Q i ( z i ) ,这个也是显而易见成立的,第三步就是使用了上面的琴生不等式了:
(1)首先log在(0, +∞ + ∞ )是凹函数,然后式 p(xi,z(i);θ)Qi(zi) p ( x i , z ( i ) ; θ ) Q i ( z i ) 由于上下式皆是正整数,假设了 Qi(zi) Q i ( z i ) 可以很小接近0但不为0;
(2)Q_i(z^{i})是概率,满足累加和为1;
(3)log函数是凹函数。
对此便可以对 p(xi,z(i);θ)Qi(zi) p ( x i , z ( i ) ; θ ) Q i ( z i ) 和log函数使用琴生不等式,故引出了式4、5。
这里我们看下式4,其实可以发现左端是 L(θ) L ( θ ) ,只与变量 θ θ 有关,如果固定了 θ θ 的话,就相当于确定了右式 ∑mi=1∑z(i)Qi(zi)logp(xi,z(i);θ)Qi(zi) ∑ i = 1 m ∑ z ( i ) Q i ( z i ) l o g p ( x i , z ( i ) ; θ ) Q i ( z i ) 的上界,而根据琴生不等式的定义,知道这个等式成立的结果需要 p(xi,z(i);θ)Qi(zi) p ( x i , z ( i ) ; θ ) Q i ( z i ) 为常数,该常数记为c。然后对于 Qi(z(i)) Q i ( z ( i ) ) 满足 ∑z(i)Qi(z(i))=1 ∑ z ( i ) Q i ( z ( i ) ) = 1 ,可推出:
及由式6和式9得:
从式11其实可以看出来我们是求了一个后验条件概率,(这里如果不是很明确的话可以留下心,后面举例子时可以再理解下公式)这也解释了我们上面提到的关于 Qi(z(i)) Q i ( z ( i ) ) 里面字母的含义了。这一步其实也就是我们常说的E步了,就我个人理解,E其实是来源于上式(4)和(5)期望的使用,这里求出的 Qi(z(i)) Q i ( z ( i ) ) 是在琴生不等式背景下固定了 θ θ 时求出来的要满足达到上界时的成立条件,最后E步的结果在M步时会用到,因为M步极大似然求导是Q是作为参数。而EM的精髓其实也就在这里了,首先我们已经明确了没有办法直接通过原始的形式为log内求和的极大似然的解析解,但是可以通过一系列变换构造出上下界关系,尽管这里这个上下界的不等式受参数 θ θ 和隐变量影响,但我们通过式11的一系列推导可以知道如果固定了参数 θ θ ,可以求出对应满足达到上界条件的一些隐变量信息,而通过这系列的隐变量信息,你是可以调整更新式子,来得到一个新的上下界信息,这时将 θ θ 看作优化参数,通过诸如求导的方式进行求解,能够得到使 L L 更大的参数 θ θ 这也就是M步了。M步的求解需要考虑到实际假设的分布,在下面的三硬币模型里面会给出例子。然后重复以上E和M的过程(坐标上升法)直到改动较小便完成了迭代。
值得注意的是,由于出现了类似鸡生蛋和蛋生鸡的关系,我们通过先初始了一个 θ θ 来进行关系打破,迭代求解,这个求解的结果是受 θ θ 的初始值影响的,我们的求解结果是一个局部优解,可以尝试更改初始值来试图找到更好的解。
EM公式的收敛性证明
上面做了很多推导,不要忘记我们最初的目的是希望能够得到一个 θ θ 来满足样本集发生最大化,所以我们需要确定我们在迭代的过程是否是朝着这个方向前进。
假设经过了t和t+1次迭代,我们得到了两个参数 θ(t) θ ( t ) 和 θ(t+1) θ ( t + 1 ) ,
式13的成立时因为使用了琴生不等式,而式14的成立是因为参数 θ(t+1) θ ( t + 1 ) 是在一次EM迭代后得到的参数,先固定了 θ(t) θ ( t ) ,求出了更合适的 Qi(z(i)) Q i ( z ( i ) ) ,在这个基础上再用了极大似然法求解出了 θ(t+1) θ ( t + 1 ) ,所以能够成立,所以这里也就能理解为什么前面M步时是可以用式5进行参数求解。而这个函数 L(θ) L ( θ ) 本身是有上界的,因为它是样本集发生概率的对数,概率上限为1,单调上升又有上界自然便是收敛的了。但没有说这个是最优解,原因还是因为对初始参数敏感。
双硬币模型解析
对于EM算法,像双硬币模型和三硬币模型都是很出名的例子,这里会对双硬币模型进行解析,
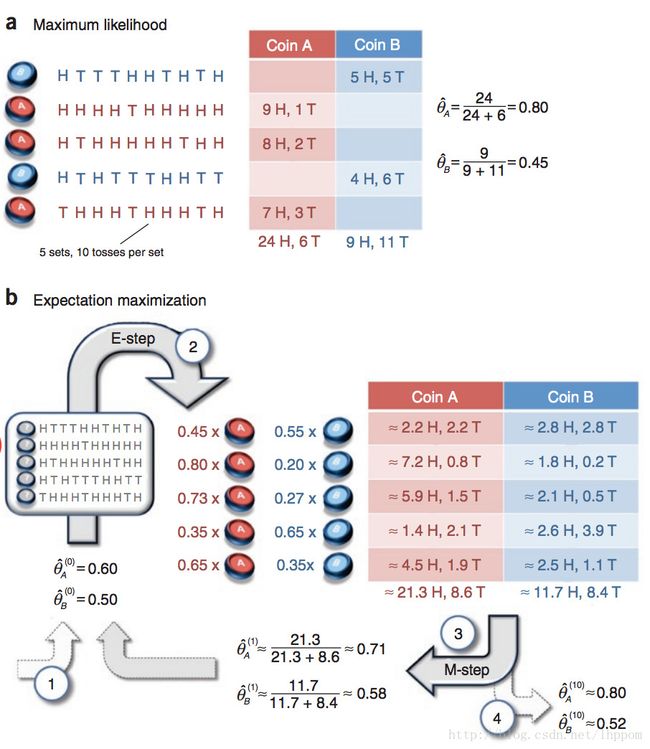
双硬币模型,5次使用两枚硬币A和B中的一枚进行抛掷,每次抛掷5次,求硬币A、B朝上和朝下的结果,如图,可以分为两种情况:
(1)一种是知道每次抛掷选择的硬币和每次硬币的朝向结果,直接使用极大似然法进行求解:
极大似然估计,使求导为0:
(2)另一种情况就是在不知道每次选择抛掷的硬币是A还是B,但是知道每次抛掷的结果序列,这时就需要使用EM算法进行求解了
E step,假设给定了初始参数为 θ(t)A^ θ A ( t ) ^ 和 θ(t)B^ θ B ( t ) ^ :
M step,假设迭代中确定了隐变量和样本的后验概率分布了即 p(zi=A|xi;θ) p ( z i = A | x i ; θ ) ,现在要通过 L=∑5i=1∑z(i)Qi(z(i))logp(x(i),z(i);θ)Qz(i)i L = ∑ i = 1 5 ∑ z ( i ) Q i ( z ( i ) ) l o g p ( x ( i ) , z ( i ) ; θ ) Q i z ( i ) 进行求导得出新的 θAt+1^ θ A t + 1 ^
注意的是我们这里的 Qi(z(i)) Q i ( z ( i ) ) 是已知变量,与求导优化参数目标 θAt+1^ θ A t + 1 ^ 无关。
令上式求导为0,得式:
能够看到这里公式的结果就是图中所示的计算方法。
总结
所以EM算法是在数学公式基础上推导出来的,首先需要构造出诸如 ∑mi=1∑z(i)Qi(z(i))logp(x(i),z(i);θ)Qi(z(i)) ∑ i = 1 m ∑ z ( i ) Q i ( z ( i ) ) l o g p ( x ( i ) , z ( i ) ; θ ) Q i ( z ( i ) ) 这样的期望形式的极大似然函数,给定一个初始参数后,先执行Estep,求出当前参数下的最佳隐变量和样本的后验概率,接着使用该概率重现调整参数,直至收敛。
参考:http://blog.csdn.net/garfielder007/article/details/51517729