基于CPU实现的Cook-Torrance光照模型(Cg语言实现)
摘抄“GPU Programming And Cg Language Primer 1rd Edition” 中文 名“GPU编程与CG语言之阳春白雪下里巴人”
在过去的一段时间中,光照模型得到了深入的发展,人们不再满足于只是对漫反射现象和镜面反射现象进行模拟,而是希望可以模拟更多特殊材质上的光照效果,如同向异性、各项异性等。上一章已经提到过,无论是漫反射,还是镜面反射,都属于材质和光交互的理想状态,就好像物理学中的无阻力状态和恒温状态,真实的情况是:漫反射和镜面反射都需要依据材质特征和物体表面微平面特征。 图 21 是实际漫反射、镜面反射与理想漫反射、镜面反射的示意图。
材质和光的交互方式是多种多样的,例如,我们可以在光盘上看到如扇面般的光带分布,在光滑的圆柱形炊具上可以看到光的条纹。为了衡量材质的光学特征和物体表面微平面特征, BRDF ( Bidirectional Reflectance Distribution Function )模型应运而生。
本章将要讲到的以 BRDF 模型为代表的一些新的光照模型,它们的共同特点是,扩展了材质和光的交互方式,充分考虑材质微平面对光的影响。
首先讲解 Cook-Torrance 光照模型,并给出 GPU 上的实现代码;然后重点阐述 BRDF 模型, BRDF 表示双向反射分布函数( Bidirectional Reflectance Distribution Function ) , 用来描述光线如何在物体表面进行反射。 BRDF 模型的概念较为复杂,其中亦有许多不同的分枝模型,中文资料中少有对该类型模型给出详细讲解和实现代码的,不过该领域的研究已经是国际上一个热点,确有学习和研究的价值。
10.1 Cook-Torrance 光照模型
使用 phong 和 blinn-phong 光照模型渲染出来的效果都存在一个问题:效果过于艺术化,不太真实。这是因为这两种模型都对材质细节方面没有进行考虑。
1981 年, Robert L. Cook 和 Kenneth E. Torrance 发表了名为 “A Reflectance Model For Computer Graphics” 的论文,首次提出了 Cook-Torrance 光照模型。
Cook-Torrance 光照模型将物体粗糙表面( rough surface )看作由很多微小平面(微平面)组成,每一个微平面都被看作一个理想的镜面反射体,物体表面的粗糙度由微平面斜率的变化来衡量。一个粗糙表面由一系列斜率变化很大的微平面组成,而在相对平滑的表面上微平面斜率变化较小。
Cook-Torrance 模型将光分为两个方面考虑:漫反射光强和镜面反射光强。如公式( 10-1 )所示:
![]()
其中 Idiff是漫反射光强,该部分的计算方法和前面所讲的相同, Ks*Il*Rs是镜面反射光强的计算方法。从公式可以看出: cook-Torrance 模型与 phong 、 blinn-phong 模型的不同之处在于 Rs 的计算方法。实际上, cook-Torrance 、 phong 和 blinn-phong 三种光照模型的本质区别都在于 “ 使用不同数学表达式计算 Rs ” 。 Rs 在英文中称之为 “ specular term ” 。
关于 Cook-Torrance 模型 的 Rs ,我找到了两个不同的数学描述。在 Wikipedia 的 specular highlight 网页中提供的计算方法为公式 ( 10-2 ) :
在《 3D 游戏与计算机图形学中的数学方法》第 117 页和 D3DBook (Lighting) Cook-Torrance 一文中给出的数学表达均为公式( 10-3 ):
我在“ A Reflectance Model For Computer Graphics ”一文中对公式的原始出处进行了查询,确定公式( 10-3 )是正确的数学表达。
F 是 Fresnel 反射系数( Fresnel reflect term ),表示反射方向上的光强占原始光强的比率; D 表示微平面分布函数( Beckmann distribution factor ),返回的是“给定方向上的微平面的分数值”; G 是几何衰减系数( Geometric attenuation term ),衡量微平面自身遮蔽光强的影响。N 、V 、L 分别表示法向量、视线方向(从顶点到视点)和入射光方向(从顶点向外)。
schlick 给出了 Fresnel 反射系数的一个近似(参阅第 11 章),精度在 1% 范围内,如公式 ( 10-4 )所示 :
Fo为入射角度接近 0 (入射方向靠近法向量)时的 Fresnel 反射系数,V 是指向视点的向量, H为半角向量。
微平面分布函数:根据给定的半角向量 H ,微平面分布函数返回微平面的分数值。最常使用的微平面分布函是 Backmann 分布函数:
m值用于度量表面的粗糙程度,较大的 m值对应于粗糙平面,较小的m 值对应与较光滑的表面; a是顶点法向量 N 和半角向量 H 的夹角。其中
所以 Backmann 微平面分布函数的最终数学表达为公式 ( 10-7 )所示 :
微平面上的入射光,在到达一个表面之前或被该表面反射之后,可能会被相邻的微平面阻挡,未被遮挡的光随机发散,最终形成了表面漫反射的一部分。这种阻挡会造成镜面反射的轻微昏暗,可以用几何衰减系数来衡量这种影响。
微平面上反射的光可能出现三种情况:入射光未被遮挡,此时到达观察者的光强为 1 ;入射光部分被遮挡;反射光部分被遮挡。几何衰减系数被定义为:到达观察者的光的最小强度。所以:
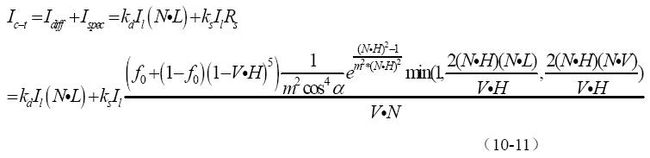
综上所述, Cook-Torrance 光照模型的 specular term 的最终数学表达为:
附:《在3D游戏与计算机图形学中的数学方法》第 119 页将 beckmann 分布函数,错写为“ Backmann ”,此外该页中给出的 beckmann 分布函数为公式 ( 10-12 ) :
我查阅论文《 A Reflectance Model For Computer Graphics 》,确认文章中给出的 D 的求法应该为公式 ( 10-7 ) 中的形式。给出图片为证。
不过,我也在国外的一些技术资料上看到类似于公式般的写法(只是把下面的 圆周率去掉了),这种写法应该是一种变体形式,本质上不会影响光强,只是对光强做一种缩放而已。 Cook-Torrance 提出之前,微平面分布函数使用的是高斯分布(即正态分布)函数。
此外,所谓的 beckmann 分布函数相关资料非常少,通过反复查询,可以确认这是电磁学中的一个分布函数,有兴趣深入研究的,可以参考如下两个资料:
1. Beckmann, Petr and Spizzichino, Andre, The Scattering of Electromagnetic Waves from Rpugh Surfaces, MacMillan, pp.1-33, 70-98, 1963;
2. Computer graphics: principles and practice, James D. Foley - 1995 - Computers - 1175 页
10.1.1 Cook-Torrance 光照模型渲染实现
Cook-Torrance 光照模型的渲染效果为 图 22 :
本节给出 Cook-Torrance 光照模型的实现代码,顶点着色程序如下所示:
代码 8 Cook-Torrance 光照模型顶点着色程序
void main_v( float4 position : POSITION,
float4 normal : NORMAL,
out float4 oPosition : POSITION,
out float3 worldPos : TEXCOORD0,
out float3 oNormal : TEXCOORD1,
uniform float4x4 worldMatrix,
uniform float4x4 worldMatrix_IT,
uniform float4x4 worldViewProj)
{
oPosition = mul(worldViewProj, position);
worldPos = mul(worldMatrix, position).xyz;
oNormal = mul(worldMatrix_IT,normal).xyz;
oNormal = normalize(oNormal);
}
片段着色程序为:
代码 9 Cook-Torrance 光照模型片段着色程序
void main_f(float3 position : TEXCOORD0,
float3 normal : TEXCOORD1,
out float4 color : COLOR,
uniform float3 globalAmbient,
uniform float3 lightColor,
uniform float3 lightPosition,
uniform float3 eyePosition,
uniform float3 Ka,
uniform float3 Kd,
uniform float3 Ks,
uniform float f,
uniform float m)
{
float3 P = position.xyz;
float3 N = normalize(normal);
float3 ambient = Ka * globalAmbient; // 计算环境光分量
float3 L = normalize(lightPosition - P);
float nl = max(dot(L, N), 0);
float3 diffuse = Kd * lightColor * nl; // 计算漫反射光分量
float3 V = normalize(eyePosition - P);
float3 H = normalize(L + V);
float3 specular = float3(0.0,0.0,0.0);
float nv = dot(N,V);
bool back = (nv>0) && (nl>0);
if(back)
{
float nh = dot(N,H);
float temp = (nh*nh-1)/(m*m*nh*nh);
float roughness = (exp(temp))/(pow(m,2)*pow(nh,4.0)); // 粗糙度,根据 beckmann 函数
float vh = dot(V,H);
float a = (2*nh*nv)/vh;
float b = (2*nh*nl)/vh;
float geometric = min(a,b);
geometric = min(1,geometric); // 几何衰减系数
float fresnelCoe=f+(1-f)*pow(1-vh,5.0); //fresnel 反射系数
float rs = (fresnelCoe*geometric*roughness)/(nv*nl);
specular = rs * lightColor * nl*Ks; // 计算镜面反射光分量(这是重点)
}
color.xyz = ambient + diffuse + specular;
color.w = 1;
}