回归分析

回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技

术通常用于预测分析以及发现变量之间的因果关系。

使用回归分析的好处良多。具体如下：
1. 它表明自变量和因变量之间的显著关系；
2. 它表明多个自变量对一个因变量的影响强度。
回归分析也允许我们去比较那些衡量不同尺度的变量之间的相互影响，如价格变动与促销活动数量
之间联系。

线性回归

线性回归模型如下式子所示：

其中权重wi和常数项b是待定的。这意味着将输入的自变量按一定的比例加权求和，得到预测值输出。

使用sklearn快速实现线性回归模型：

➢ sklearn.linear_model中的LinearRegression可实现线性回归
➢ LinearRegression 的构造方法：
➢ sklearn.linear_model.LinearRegression(fit_intercept=True #默认值为 True，表示 计算随机变量，False 表示不计算随机变量, normalize=False #默认值为 False， 表示在回归前是否对回归因子 X 进行归一化)
➢ LinearRegression 的属性有：coef_和intercept_。 coef_存储w1 到wp 的值，与X 的维数一致。intercept_存储w0（b）的值。 

LinearRegression 的常用方法有：

➢ decision_function(X) #返回 X 的预测值 y
➢ fit(X,y[,n_jobs]) #拟合模型  (X对应列表)
➢ get_params([deep]) #获取 LinearRegression 构造方法的参数信息
➢ predict(X) #求预测值 #同 decision_function
➢ score(X,y[,sample_weight]) #确定性系数（ R2），计算公式为：

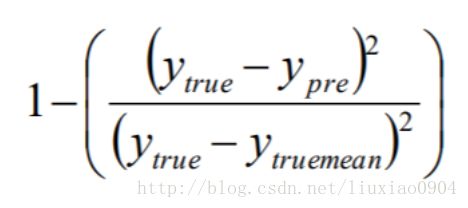
取值在[0，1]之间。越接近1，表明方程中的变量对y的解释能力越强。通常将R2乘以100%表示回归方程解释y变化的百分比。
➢ set_params(**params) #设置 LinearRegression 构造方法的参数值 

练手：

from sklearn.linear_model import LinearRegression
x = [[i,i] for i in range(3)]
y = [0, 1, 2]
lm = LinearRegression()
lm.fit(x, y)
print(lm.predict([[3,3]]))
print(lm.coef_)
print(lm.intercept_)
print(lm.score(x,y))

x = [[i] for i in range(1,5)]
y = [1, 4, 9, 12]
lm = LinearRegression()
lm.fit(x, y)
print(lm.predict([[5]]))
#系数（斜率）
print(lm.coef_)
#x0(截距)
print(lm.intercept_)
print('拟合得到的方程为：y= ',lm.coef_,'*x +',lm.intercept_)
print(lm.score(x, y))

对波士顿房价数据集实现线性回归分析：

为了便于学习，使用data中的第五列（房间数）实现一维的分析

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
boston = load_boston()
print(boston.keys())
x = boston.data[:, 5]
print(x[:5])
#此时x为一个array,为线性回归分析需要把它变为列表（列表表达式）
x1 = [[float(str(i))] for i in x]  # 为避免6.575转为浮点型数据，在这里先转为字符串再转为浮点型数据
print(x1[:5])
y = boston.target
lm = LinearRegression()
lm.fit(x1, y)
print('回归方程的确定性系数为：', lm.score(x1, y))
print('回归方程的斜率为：', lm.coef_)
print('回归方程的截距为：', lm.intercept_)
print('回归方程为：y = ', lm.coef_, '*x + (', lm.intercept_, ')')

import matplotlib.pyplot as plt
plt.scatter(x, y)
plt.scatter(x, lm.predict(x1), color='red')
plt.plot(x, x*lm.coef_ + lm.intercept_, color='green')
plt.show()

逻辑回归

➢ 准确地说，逻辑回归（Logistic Regression）是对数几率回归，属于广义线性模型（GLM），它的因变量一般只有0或1.
➢ 需要明确一件事情：线性回归并没有对数据的分布进行任何假设，而逻辑回归隐含了一个基本假设 ：每个样本均独立服从于伯努利分布（0-1分布）。
➢ 伯努利分布属于指数分布族，这个大家庭还包括：高斯（正态）分布、多项式分布、泊松分布、伽马分布、 Dirichlet分布等。 

逻辑回归仅对较大数据量时比较友好

使用sklearn快速调用逻辑回归模型：

➢ from sklearn.linear_model import LogisticRegression
➢ LogisticRegression() # 构建模型
➢ 方法：
• fit(x, y) # 训练
• predict(x) # 测试
• score() # 评价 

数据预处理——离散数据编码

➢ 离散特征的编码分为两种情况：
1、离散特征的取值之间没有大小的意义，比如color：[red,blue]，那么就使用one-hot编码
2、离散特征的取值有大小的意义，比如size:[X,XL,XXL],那么就使用数值的映射{X:1,XL:2,XXL:3}
➢ 独热编码即 One-Hot 编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，
每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。

数据预处理——独热编码（one-hot encoding） 

➢ 使用pandas的get_dummies函数进行one-hot编码
➢ get_dummies(data, prefix=None, prefix_sep='_', dummy_na=False, columns=None,
sparse=False, drop_first=False)
➢ data：数据（数组或者数据框）
➢ prefix：默认为None，如果是列名，则表示字符串传递长度等于在DataFrame上调用get_dummies时的
列数的列表
➢ columns：要编码的DataFrame中的列名。如果列是None，那么所有与列对象或类别 D型细胞将被转换。

sklearn. model_selection.train_test_split随机划分训练集和测试集

➢ train_test_split是交叉验证中常用的函数，功能是从样本中随机的按比例选取train data和testdata，形式为：
➢ X_train,X_test, y_train, y_test = model_selection.train_test_split(train_data, train_target,test_size=0.4（train_size=0.6）, random_state=0)

train_test_split参数解释：

➢ train_data：所要划分的样本特征集
➢ train_target：所要划分的样本结果
➢ test_size：样本占比，如果是整数的话就是样本的数量
➢ random_state：是随机数的种子。
• 随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你
每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。
• 随机数的产生取决于种子，随机数和种子之间的关系遵从以下两个规则：
• 种子不同，产生不同的随机数；种子相同，即使实例不同也产生相同的随机数。

练手：研究生是否被录取的逻辑回归分析：

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import pandas as pd
#混淆矩阵
from sklearn.metrics import confusion_matrix
import os

os.chdir('D:\\学习\\数据挖掘\\泰迪培训\\回归')
data = pd.read_csv('LogisticRegression.csv')
print(data.head())
#对rank进行独热编码
data_dum = pd.get_dummies(data, columns=['rank'])
print(data_dum.head())
#train_test_split是交叉验证中常用的函数，功能是从样本中随机的按比例选取traindata和testdata
x_train, x_test, y_train, y_test = train_test_split(data_dum.ix[:, 1:], data_dum.ix[:, 0], random_state=520, test_size=0.1)
#建立逻辑回归模型
lr = LogisticRegression()
#用训练集拟合模型
lr.fit(x_train, y_train)
print(lr.predict(x_test))
#混淆矩阵结果：
#[[27  4]
# [ 6  3]]
#表示27+3个预测正确，6+4个预测错误
print(confusion_matrix(y_test, lr.predict(x_test)))

print('正确率为：{}%'.format(lr.score(x_test,y_test)*100))