Python概率分布大全（含可视化）

术语

1. pdf，概率密度函数（Probability Density Function），连续型随机变量的概率。
2. cdf，累积分布函数（Cumulative Distribution Function），pdf的积分。
3. ppf，百分点函数（Percent Point Function），cdf的倒数。
4. pmf，概率质量函数（Probability Mass Function），离散型随机变量的概率。

正态分布的各种函数

前言

使用numpy.random.generator的Generator类

默认导入

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline

rng = np.random.default_rng()  # 构造一个默认位生成器(PCG64)

整数

integers(low, high=None, size=None, dtype='int64', endpoint=False)

low下限，high上限，取值 [low, high)

endpoint=True时取值 [low, high]

size尺寸或形状

print(rng.integers(low=0, high=10, size=10))  # [0,10)的10个随机整数
print(rng.integers(low=0, high=10, size=10, endpoint=True))  # [0,10]的10个随机整数
print(rng.integers(low=0, high=10, size=(2, 4)))  # 形状为(2, 4)
print(rng.integers(low=0, high=[1, 10, 100]))  # 上限不同
# [3 8 4 2 7 1 1 9 7 4]
# [ 9 10  8  1  7  3  7  8  8  6]
# [[4 4 1 2]
#  [2 6 3 8]]
# [0 9 2]

浮点数

random(size=None, dtype='d', out=None)

size尺寸或形状

print(rng.random(size=10))  # [0.0, 1.0)的10个随机浮点数
print(rng.random(size=(2, 4)))  # 形状为(2, 4)
# [0.6986286  0.7083849  0.86588093 0.63301974 0.89362993 0.97340382 0.79295529 0.14079166 0.50348895 0.73972237]
# [[0.54939163 0.04432164 0.6797271  0.49858971]
#  [0.3781034  0.89830482 0.06314135 0.25944355]]

low = 0
high = 10
print((high-low)*rng.random(size=10)+low)  # [0.0, 10.0)的10个随机浮点数
# [8.92076148 8.11545414 9.34270912 4.95565778 0.88044604 7.9555204 3.3780767  7.9214436  3.64540636 1.29831035]

抽取

choice(a, size=None, replace=True, p=None, axis=0)

a 抽取范围 int或1维数组

size尺寸或形状

replace是否放回原处

p 每个元素的抽取概率 1维数组

print(rng.choice(a=10, size=3))  # [0,10)的3个随机整数，a=10调用了np.arange(10)，相当于rng.integers(low=0, high=10, size=3)
print(rng.integers(low=0, high=10, size=3))
# [2 6 0]
# [8 4 4]

print(rng.choice(a=[1,2,3,4,5], size=5))  # 从中抽3个
print(rng.choice(a=[1,2,3,4,5], size=5, replace=False))  # 不放回
# [1 2 2 5 2]
# [5 4 1 3 2]

字节

bytes(length)

print(rng.bytes(10))
# b'\xf7\x8f@{\x9d\xbb\xdfk\x9c\x97'

洗牌

shuffle(x)返回空值，影响原数组

l = np.arange(10)  # list也行
print(l)
rng.shuffle(l)
print(l)
# [0 1 2 3 4 5 6 7 8 9]
# [6 8 9 2 0 3 5 4 7 1]

排列

permutation(x)类似洗牌，只影响最外层

x int或数组

print(rng.permutation(10))  # 随机排列0-9的数组
print(rng.permutation(np.arange(10)))  #同上
# [7 8 6 0 2 1 9 3 4 5]
# [0 5 7 2 8 6 4 3 9 1]

arr = np.arange(9).reshape((3, 3))
print(arr)
print(rng.permutation(arr))  # 只影响最外层的顺序
print(arr)
# [[0 1 2]
#  [3 4 5]
#  [6 7 8]]
# [[3 4 5]
#  [6 7 8]
#  [0 1 2]]
# [[0 1 2]
#  [3 4 5]
#  [6 7 8]]

贝塔分布

beta(a, b, size=None)

贝塔分布是狄利克雷分布的特例，与伽马分布有关。

贝塔分布是伯努利分布和二项式分布的共轭先验分布的密度函数，也称B分布，是一组定义在(0,1)的连续概率分布（概率的概率分布）。

概率分布函数：

$f\left(x;\alpha ,\beta \right)=\frac{1}{\text{B}\left(\alpha ,\beta \right)}{x}^{\alpha -1}{\left(1-x\right)}^{\beta -1}$

随机变量$X$服从参数为$\alpha ,\beta$的B分布写作

$\text{X Be}\left(\alpha ,\beta \right)$

常用于贝叶斯推理和顺序统计问题

print(rng.beta(a=0.5, b=0.5, size=5))
# [0.08319717 0.99990539 0.27823195 0.43770009 0.92379961]

二项分布

binomial(n, p, size=None)

二项分布是重复n次的独立的伯努利试验（事件发生概率为p），每次试验相互独立，如抛硬币。

概率密度函数：

$P\left(N\right)=\left(\begin{array}{c}n\\ N\end{array}\right)p^N{\left(1-p\right)}^{n-N}$

其中n是试验次数，p是成功的概率，N是成功的次数。

print(rng.binomial(n=100, p=0.5, size=1)) # 抛100次硬币，重复1次
# [56]

卡方分布

chisquare(df, size=None)

df（自由度数）是独立随机变量，每个变量是标准正态分布（均值为0，方差为1），将其进行平方求和，得到卡方分布。

概率密度函数：

$p\left(x\right)=\frac{{\left(1/2\right)}^{k/2}}{\Gamma \left(k/2\right)}{x}^{k/2-1}{e}^{-x/2}$

其中$\Gamma$是伽马函数：

$\Gamma \left(x\right)={\int }_0^{-\infty }{t}^{x-1}{e}^{-t}dt$

常用于假设检验。

print(rng.chisquare(df=2, size=4))
# [0.34648411 1.91586176 4.13172809 1.02655846]

性别与宠物偏爱是否有关

列联表

	猫	狗
男	207	282
女	231	242

列联表2行2列，则自由度df=(r-1)(c-1)=(2-1)*(2-1)=1

x = [[207, 282], [231, 242]]
chi2, p, df, expected = stats.chi2_contingency(x, correction=False)  # 结果分别为：卡方值、P值、自由度、理论值，无需耶茨连续性修正
value = stats.chi2.ppf(0.95, df=df)  # 变量相关概率为0.95时对应的卡方值
print('自由度{}'.format(df))
print('数据卡方值{:.2f}大于变量相关为0.95的卡方值{:.2f}'.format(chi2, value))
print('因此变量相关的可能性大于0.95')
print('变量相关的可能性具体为{:.2f}'.format(1-p))

# 自由度1
# 数据卡方值4.10大于变量相关为0.95的卡方值3.84
# 因此变量相关的可能性大于0.95
# 变量相关的可能性具体为0.96

狄利克雷分布

狄利克雷分布是贝塔分布在高维的推广，常作为贝叶斯统计的先验概率。

概率密度函数：

$\text{Dir}\left(\text{X|}\alpha \right)=\frac{1}{\text{B}\left(\alpha \right)}{\prod }_{i-1}^K{x}_i^{{\alpha }_i-1}$

$\text{B}\left(\alpha \right)=\frac{{\prod }_{i-1}^{\text{K}}\Gamma \left({\alpha }_i\right)}{\Gamma \left({\sum }_{i=1}^{\text{K}}{\alpha }_i\right)}$

$\alpha =\left({\alpha }_1,...,{\alpha }_{\text{K}}\right)$

常用于自然语言处理，特别是主题模型的研究。

print(rng.dirichlet(alpha=(10, 5, 3), size=3))
# [[0.45682216, 0.15384054, 0.3893373 ],
#  [0.41066417, 0.35596082, 0.23337501],
#  [0.62489734, 0.17707421, 0.19802845]]

指数分布

exponential(scale=1.0, size=None)

指数分布是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。

概率密度函数：

$f\left(x;\lambda \right)=\lambda e^{-\lambda x},x\ge 0$

其中$\lambda$为单位时间发生的次数。

常用于预估电子产品寿命，页面请求间的时间间隔。

print(rng.exponential(scale=1.0, size=3))
# [0.48583027, 1.45895053, 1.30734696]

print('某产品平均10年发生一次重大故障，要求保修的比例不超过20%，请问应设几年质保？过10年后，约有多少产品发生重大故障？')
la = 1/10  # 发生概率
print('{:.2f}年'.format(stats.expon.ppf(0.2, scale=1/la)))
print('{:.2f}%的产品发生重大故障'.format(stats.expon.cdf(10, scale=1/la)*100))

# 某产品平均10年发生一次重大故障，要求保修的比例不超过20%，请问应设几年质保？过10年后，约有多少产品发生重大故障？
# 2.23年
# 63.21%的产品发生重大故障

F分布

f(dfnum, dfden, size=None)

dfnum分子自由度，dfden分母自由度。

F分布是一种非对称连续概率分布，有两个自由度，且位置不可互换。

F分布的随机变量是两个卡方分布除以自由度：

$\frac{U_1/d_1}{U_2/d_2}=\frac{U_1/U_2}{d_1/d_2}$

概率密度函数：

$f\left(x;d_1,d_2\right)=\frac{\sqrt{\frac{{\left(d_{1}x\right)}^{d_1}{d}_2^{d_2}}{{\left(d_{1}x+d_2\right)}^{d_1+d_2}}}}{x\text{B}\left(\frac{d_1}{2},\frac{d_2}{2}\right)}$

常用于方差分析，回归方程的显著性检验。

print(rng.f(dfnum=2, dfden=2, size=3))
# array([1.57466637, 0.33761916, 0.19025353]

伽玛分布

gamma(shape, scale=1.0, size=None)

伽玛分布是一种连续型概率分布，$\alpha$为形状参数，$\beta$为尺度参数。指数分布和卡方分布都是伽玛分布的特例。

假设${\text{X}}_1,{\text{X}}_2,...,{\text{X}}_{\text{n}}$为连续发生事件的等候时间，且这n次等候时间独立，那么这n次等候时间之和Y服从伽玛分布，即$\text{Y}\sim \Gamma \left(\alpha ,\beta \right)$，其中$\alpha =n,\beta =\lambda$

概率密度函数：

$f\left(x\right)=\frac{x^{\left(\alpha -1\right)}{\beta }^{\alpha }{e}^{\left(-\beta x\right)}}{\Gamma \left(\alpha \right)},x>0$

其中$\Gamma \left(\alpha \right)$为：

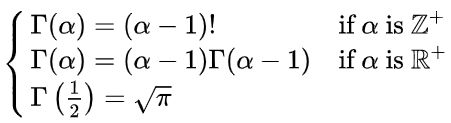
print(rng.gamma(shape=2, scale=2, size=3))  # shape即alpha，scale即beta
# [4.34964442, 6.21444278, 4.25584051]

几何分布

geometric(p, size=None)

几何分布是一种离散型概率分布。在n次伯努利试验中，前k-1次都失败，第k次成功的概率。如不停地掷骰子直到掷到1是一个p=1/6的几何分布。

概率质量函数：

$f\left(x\right)={\left(1-p\right)}^{x-1}p,x=1,2,...$

print(rng.geometric(p=0.2, size=10))
# [ 4  1  7  1 14  5  1  5  3  7]

耿贝尔分布

gumbel(loc=0.0, scale=1.0, size=None)

耿贝尔分布是一种连续型概率分布，模拟不同分布的最大值(或最小值)的分布。$\mu$为中心参数，$\beta$为展宽参数。

概率密度函数：

$f\left(x\right)=\frac{1}{\beta }{e}^{-\left(z+e^{-z}\right)}$

其中$z=\frac{x-\mu }{\beta }$

常用于多年一遇事件，最大风速计算，极端潮位，预测地震洪水或其他自然灾害发生的几率等。

mu = 0
sigma = 0.1
print(rng.gumbel(loc=mu, scale=sigma, size=3))
# [ 0.08178895  0.35426048 -0.02772167]

print('某气象站100年的最大风速经验分布曲线如图，估计最大风速大于26.2m/s的再现期和50年一遇的再现极值。')
mu = 23.6
beta = 1.0
print('最大风速大于26.2m/s的再现期为{:.2f}年'.format(1 / (1 - stats.gumbel_r.cdf(26.2, loc=mu, scale=beta))))
print('50年一遇的再现极值为{:.2f}m/s'.format(stats.gumbel_r.ppf(1 - 1 / 50, loc=mu, scale=beta)))
# 某气象站100年的最大风速经验分布曲线如图，估计最大风速大于26.2m/s的再现期和50年一遇的再现极值。
# 最大风速大于26.2m/s的再现期为13.97年
# 50年一遇的再现极值为27.50m/s

超几何分布

hypergeometric(ngood, nbad, nsample, size=None)

超几何分布是一种离散型概率分布，不放回抽样。

二项分布和几何分布均基于伯努利试验，即每次试验概率不变，而超几何分布的概率会随着每一次试验而改变。

概率质量函数：

$P\left(X=k\right)=\frac{C_M^k{C}_{N-M}^{n-k}}{C_N^n},k\in \left\{0,1,2...\min \left(n,N\right)\right\}$

抽到正例数k，正反例总数M，正例总数n，抽样次数N，则：

$p\left(k,M;n;N\right)=\frac{\left(\begin{array}{c}n\\ k\end{array}\right)\left(\begin{array}{c}M-n\\ N-k\end{array}\right)}{\left(\begin{array}{c}M\\ N\end{array}\right)}$

常用于抽奖、质检。

print(rng.hypergeometric(ngood=100, nbad=20, nsample=10, size=3)) # 从100个正例20个反例中抽10个样本，抽到正例的个数
# [8 7 8]

print('箱子里一共10个球，6个黑色，4个白色，不放回抽5次，其中有3个是黑球的概率')
print(stats.hypergeom.pmf(k=3, M=10, n=6, N=5))
# 箱子里一共10个球，6个黑色，4个白色，不放回抽5次，其中有3个是黑球的概率
# 0.4761904761904759

print(rng.hypergeometric(ngood=100, nbad=20, nsample=10, size=3)) # 从100个正例20个反例中抽10个样本，抽到正例的个数
# [8 7 8]

print('箱子里一共10个球，6个黑色，4个白色，不放回抽5次，其中有3个是黑球的概率')
print(stats.hypergeom.pmf(k=3, M=10, n=6, N=5))
# 箱子里一共10个球，6个黑色，4个白色，不放回抽5次，其中有3个是黑球的概率
# 0.4761904761904759

拉普拉斯分布（双指数分布）

laplace(loc=0.0, scale=1.0, size=None)

拉普拉斯分布与正态分布相似，但峰值更尖锐，尾部更宽。它表示两个独立的、恒等分布的指数随机变量间的差。

概率密度函数：

$f\left(x;\mu ,\lambda \right)=\frac{1}{2b}\exp \left(-\frac{|x-\mu |}{b}\right)$

其中，$\mu$为位置参数，$\lambda$为尺度参数。

常用于建立经济模型和生命科学模型。

print(rng.laplace(loc=0.0, scale=1.0, size=3))
# [-0.07861936 -0.00814725 -1.64295374]

逻辑斯谛分布

logistic(loc=0.0, scale=1.0, size=None)

逻辑斯谛分布用于极值问题，在流行病学中可作为耿贝尔分布的混合。在国际象棋协会的埃洛等级分系统中，假设每个棋手的表现是一个逻辑斯谛分布的随机变量。

概率密度函数：

$P\left(x\right)=\frac{e^{-\left(x-\mu \right)/s}}{s{\left(1+e^{-\left(x-\mu \right)/s}\right)}^2}$

其中，$\mu$为位置参数，$s$为尺度参数。

常用于逻辑回归，电子传导，河流流量和降雨量的分布，游戏评级。

print(rng.logistic(loc=10, scale=1, size=3))
# [ 9.07819078 14.01816903 11.36678804]

正态分布（高斯分布）

normal(loc=0.0, scale=1.0, size=None)

正态分布是一种连续型概率分布，$\mu$为位置参数，$\sigma$为尺度参数。正态分布在自然界中很常见，如身高、寿命、考试成绩等，属于各种因素相加对结果的影响。

若随机变量$X$服从一个数学期望为$\mu$，方差为${\sigma }^2$的正态分布，记为$N\left(\mu ,{\sigma }^2\right)$

$\mu =0,\sigma =1$的正态分布是标准正态分布。

常用于频数分布，估计参考值范围。

print(rng.normal(loc=0, scale=0.1, size=3))
# [-0.18035931  0.05842693 -0.11583966]

print('一次考试成绩近似服从正态分布N(70,10²)，第100名成绩为60分，问第20名成绩约为多少？')
scale = 1-stats.norm.cdf(60, loc=70, scale=math.sqrt(100))
print('60分以上占比{:.2f}%'.format(scale*100))
print('学生总数{}'.format(round(100/scale)))
print('第20名成绩约为{:.2f}'.format(stats.norm.ppf(1-20/119, loc=70, scale=math.sqrt(100))))
# 一次考试成绩近似服从正态分布N(70,10²)，第100名成绩为60分，问第20名成绩约为多少？
# 60分以上占比84.13%
# 学生总数119.0
# 第20名成绩约为79.62

对数正态分布

lognormal(mean=0.0, sigma=1.0, size=None)

对数正态分布与正态分布十分相似，不过各种因素对结果的影响不是相加，而是相乘。如财富分配，图像有条长尾。

如果$Y$是正态分布的随机变量，则$e^Y$为对数正态分布；同样，如果$X$是对数正态分布，则$\ln X$为正态分布。

概率密度函数：

$f\left(x;\mu ,\sigma \right)=\frac{1}{\sigma x\sqrt{2\pi }}{e}^{-{\left(\ln x-\mu \right)}^2/2{\sigma }^2}$

其中，$\mu$为原正态分布的均值，$\sigma$为原正态分布的标准差。

常用于描述增长率。

print(rng.lognormal(mean=3, sigma=1, size=3))
# [15.13344315 50.59902961 32.16071275]

对数分布

logseries(p, size=None)

对数分布是一种离散型概率分布，也称对数级数分布。

概率质量函数：

$f\left(k\right)=-\frac{p^k}{k\log \left(1-p\right)}$

常用于物种丰富度，群体遗传学。

print(rng.logseries(p=0.6, size=3))
# [1 5 1]

多项分布

multinomial(n, pvals, size=None)

多项分布是二项分布的多元推广，如扔骰子。

概率质量函数：

$f\left(k\right)=\frac{n!}{x_1!\cdots x_k!}{p}_1^{x_1}\cdots p_k^{x_k}$

PS：scipy.stats.multinomial的项个数为2时和scipy.stats.binom的结果数值有微小区别。

 print(rng.multinomial(n=20, pvals=[1/6]*6, size=1))
 # [[5 4 1 5 3 2]]

多元正态分布

multivariate_normal(mean, cov, size=None, check_valid='warn', tol=1e-8)

多元正态分布是正态分布的高维推广，图像由均值和协方差矩阵决定。

概率密度函数：

$f\left(x\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^k\det \sum }}\exp \left(-\frac{1}{2}{\left(x-\mu \right)}^T\sum {}^{-1}\left(x-\mu \right)\right)$

其中$\mu$是均值，$\sum$是协方差矩阵，$k$是空间维度。

print(rng.multivariate_normal(mean=[0, 0], cov=[[1, 0], [0, 100]], size=3))
# [[ 0.12416816 -0.02380272]
#  [-0.31780928 -7.48949632]
#  [ 0.22960821 -3.3463358 ]]

负二项分布

negative_binomial(n, p, size=None)

负二项分布是一种离散型概率分布，成功即失败。持续到n次成功，n为正整数时，又称帕斯卡分布。

如果一个人重复掷一个骰子，直到第三次出现一个“1”，那么在第三个“1”之前出现的非“1”的数目的概率分布就是一个负的二项分布。

概率质量函数：

$P\left(N;n,p\right)=\frac{\Gamma \left(N+n\right)}{N!\Gamma \left(n\right)}{p}^n{\left(1-p\right)}^N$

print(rng.negative_binomial(n=1, p=0.1, size=3))  # N次成功前的失败次数
# [6 5 2]

非中心卡方分布

noncentral_chisquare(df, nonc, size=None)

概率密度函数：

$P\left(x;df,nonc\right)={\sum }_{i=0}^{\infty }\frac{e^{-nonc/2}{\left(nonc/2\right)}^i}{i!}{P}_{Y_{df+2i}}\left(x\right)$

常用于概率比测试。

print(rng.noncentral_chisquare(df=3, nonc=20, size=3))
# [50.45799021 19.72854198 21.81618964]

非中心F分布

noncentral_f(dfnum, dfden, nonc, size=None)

print(rng.f(dfnum=3, dfden=20, size=3))
# [0.09066648 1.28933149 0.6907764 ]

帕累托分布（Lomax Distribution）

pareto(a, size=None)

帕累托分布（II型）在现实世界的许多问题中都很有用，经典的二八定律。

概率密度函数：

$\text{P}\left(X>x\right)={\left(\frac{x}{x_{\min }}\right)}^{-k}$

常用于经济学领域如财富分配，除外它还被称为布拉德福分布，用于保险、web页面访问统计、油田大小、项目下载频率，即厚尾分布。

print((rng.pareto(a=3, size=3) + 1) * 2)
# [2.55435742 2.22068143 2.01434631]

泊松分布

poisson(lam=1.0, size=None)

泊松分布是$N$非常大的情况下二项分布的极限。

概率质量函数：

$f\left(k\right)=\frac{e^{-\mu }{\mu }^k}{k!}$

$\mu$是单位时间（或单位面积）内随机事件的平均发生率。

常用于描述单位时间（或空间）内随机事件发生的次数。如汽车站台的候客人数，机器出现的故障数，自然灾害发生的次数，一块产品上的缺陷数，显微镜下单位分区内的细菌数等。

print(rng.poisson(lam=5, size=3))
# [5 3 4]

print('某城市一周内发生交通事故的次数为参数为0.3的泊松分布，求一周内恰好发生2次交通事故的概率，求一周内至少发生1次交通事故的概率。')
print('一周内恰好发生2次交通事故的概率为{:.2f}%'.format(stats.poisson.pmf(2, mu=0.3)*100))
print('一周内至少发生1次交通事故的概率为{:.2f}%'.format((1-stats.poisson.cdf(0, mu=0.3))*100))
# 一周内恰好发生2次交通事故的概率为3.33%
# 一周内至少发生1次交通事故的概率为25.92%

幂律分布

power(a, size=None)

概率密度函数：

$P\left(x;a\right)=a{x}^{a-1},0\le x\le 1,a>0$

print(rng.power(a=5, size=3))
# [0.76505117 0.91183632 0.80631314]

瑞利分布

rayleigh(scale=1.0, size=None)

当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。

概率密度函数：

$f\left(x\right)=\frac{x}{{\sigma }^2}{e}^{-\frac{x^2}{2{\sigma }^2}},x>0$

常用于无线网络，信号处理领域。

print(rng.rayleigh(scale=3, size=3))
# [3.43910711 5.13314726 2.74963828]

柯西分布（洛伦兹分布）

standard_cauchy(size=None)

柯西分布是一个数学期望不存在的连续型概率分布。

概率密度函数：

$P\left(x;x_0,\gamma \right)=\frac{1}{\pi \gamma \left[1+{\left(\frac{x-x_0}{\gamma }\right)}^2\right]}$

$x_0=0,\gamma =1$的柯西分布是标准柯西分布。

print(rng.standard_cauchy(size=3))
# [-2.55997856  4.97604813 -0.03263361]

标准指数分布

standard_exponential(size=None, dtype='d', method='zig', out=None)

即尺度参数为1的指数分布。

print(rng.standard_exponential(size=3))
# [1.9475     0.1347515  0.79339464]

标准伽马分布

standard_gamma(shape, size=None, dtype='d', out=None)

即尺度参数为1的伽马分布。

print(rng.standard_gamma(shape=2, size=3))
# [0.83710462 2.53419793 6.09632976]

标准正态分布

standard_normal(size=None, dtype='d', out=None)

即均值为0标准差为1的正态分布。

print(rng.standard_normal(size=3))
# [0.44110815 1.33120662 1.12587407]

学生t分布

standard_t(df, size=None)

概率密度函数：

$P\left(x,df\right)=\frac{\Gamma \left(\frac{df+1}{2}\right)}{\sqrt{\pi df}\Gamma \left(\frac{df}{2}\right)}{\left(1+\frac{x^2}{df}\right)}^{-\left(df+1\right)/2}$

t检验假设数据服从正态分布，检验样本均值是否是真实均值。

t分布用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知（例如在样本数量足够多时），则应该用正态分布来估计总体均值。

print(rng.standard_t(df=10, size=3))
# [ 0.74005099 -1.86647702  0.04562169]

三角形分布（辛普森分布）

triangular(left, mode, right, size=None)

三角形分布是低限为l，众数为m，上限为r的连续概率分布。

概率密度函数：

$P\left(x;l,m,r\right)=\{\begin{array}{l}\frac{2\left(x-l\right)}{\left(r-l\right)\left(m-l\right)},l\le x\le m\\ \frac{2\left(r-x\right)}{\left(r-l\right)\left(r-m\right)},m\le x\le r\end{array}$

常用于商务决策和项目管理。

print(rng.triangular(left=-3, mode=0, right=8, size=3))
# [ 2.35825004  1.29817527 -1.23566561]

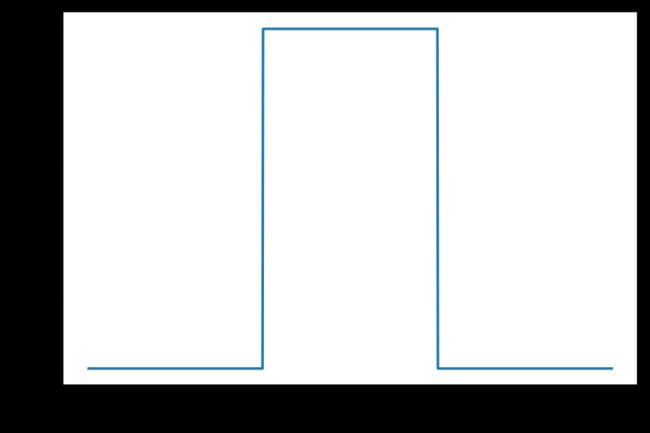
均匀分布

uniform(low=0.0, high=1.0, size=None)

概率密度函数：

$p\left(x\right)=\frac{1}{b-a}$

print(rng.uniform(low=-1, high=0, size=3))
# [-0.91576092 -0.00161295 -0.1352355 ]

冯·米塞斯分布（循环正态分布）

vonmises(mu, kappa, size=None)

概率密度函数：

$f\left(x;u,\kappa \right)=\frac{e^{\kappa }\cos \left(x-\mu \right)}{2\pi I_0\left(\kappa \right)}$

print(rng.vonmises(mu=0, kappa=4, size=3))
# [0.10144748 0.53051083 0.33354707]

逆高斯分布（Wald Distribution）

wald(mean, scale, size=None)

逆高斯分布描述布朗运动达到一个固定的正水平所需要的时间分布。

概率密度函数：

$f\left(x;\mu ,\lambda \right)=\sqrt{\frac{\lambda }{2\pi x^3}}\exp \left(-\frac{\lambda {\left(x-\mu \right)}^2}{2{\mu }^{2}x}\right)$

常用于寿命试验，卫生科学，精算学，生态学，昆虫学。

print(rng.wald(mean=3, scale=2, size=3))
# [ 0.23712345  2.06903186 26.01138062]

韦伯分布

weibull(a, size=None)

概率密度函数：

$p\left(x\right)=\frac{a}{\lambda }{\left(\frac{x}{\lambda }\right)}^{a-1}{e}^{-{\left(x/\lambda \right)}^a}$

$a=1$时，韦伯分布为指数分布。$a=2$时，韦伯分布为瑞利分布。

常用于可靠性分析和寿命检验。

print(rng.weibull(a=5, size=3))
# [0.54189045 0.92339566 0.47417438]

齐夫分布

zipf(a, size=None)

概率质量函数：

$p\left(x\right)=\frac{x^{-a}}{\zeta \left(a\right)}$

其中$\zeta$是黎曼函数。

齐夫定律表述为：在自然语言的语料库里，一个单词出现的频率与它在频率表里的排名成反比。

常用于语言学，情报学，地理学，经济学。

print(rng.zipf(a=2, size=3))
# [5 1 2]

参考文献

1. Random Generator
2. Matplotlib 教程
3. scipy.stats
4. matplotlib.pyplot
5. 百度百科
6. 带你理解beta分布
7. Chi-Square Statistic
8. How to Calculate Critical Values for Statistical Hypothesis Testing with Python
9. 结合日常生活的例子，了解什么是卡方检验
10. 卡方检验
11. Python - 列联表的独立性检验（卡方检验）
12. 人人都会数据分析
13. 正态分布为什么常见？
14. Wolfram MathWorld
15. 幂律分布背后的数学逻辑，了解一下？
16. Exploring Normal Distribution With Jupyter Notebook

绘图代码

导入

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline

rng = np.random.default_rng()  # 构造一个默认位生成器(PCG64)

术语

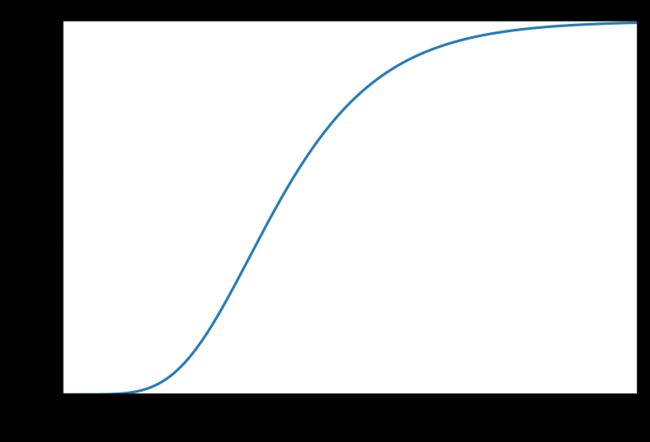
x = np.linspace(-1.5, 1.5, 100)
labels = []
f_list = [stats.norm.pdf, stats.norm.cdf, stats.norm.ppf]
plt.figure(dpi=150)
for f in f_list:
    labels.append(f)
    y = f(x, loc=0, scale=0.5)  #标准正态分布，均值0，标准差0.5
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=['pdf', 'cdf', 'ppf'], loc='best')

整数

x = rng.integers(low=0, high=10, size=1000, endpoint=True)  # [0,10]的1000个随机整数
y = np.zeros(1000)
plt.yticks([])  #去掉y轴
plt.axis([-2, 12, -1, 1])  # X∈[-2,12], Y∈[-1,1]
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.tick_params(axis='both', labelsize=14)  # 改字体
plt.plot(x, y)

浮点数

x = rng.random(size=1000)  # [0.0, 1.0)的1000个随机浮点数
y = np.zeros(1000)
plt.yticks([])
plt.axis([-0.2, 1.2, -1, 1])
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)

抽取

x = rng.choice(a=100, size=50)  # [0,100)的50个随机整数
y = np.zeros(50)
plt.yticks([])
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.tick_params(axis='both', labelsize=14)
plt.scatter(x, y)

洗牌

# color = ['red', 'orange', 'yellow', 'green', 'cyan', 'blue', 'purple']  # 红橙黄绿青蓝紫
color = ['black', 'dimgray', 'gray', 'darkgray', 'silver', 'lightgray', 'whitesmoke']  # 颜色越来越浅
x = np.arange(len(color))
y1 = np.ones(len(color))
y2 = np.zeros(len(color))
plt.axis([-0.5, 6.5, -0.5, 1.5])
plt.axis('off')  #去掉坐标轴
plt.scatter(x, y1, s=500, color=color)
rng.shuffle(color)  # 洗牌
plt.scatter(x, y2, s=500, color=color)

贝塔分布

x = np.linspace(0, 1, 100)
labels = []
a_list, b_list = [0.5, 5, 1, 2, 2], [0.5, 1, 3, 2, 5]
plt.figure(dpi=150)
for a, b in zip(a_list, b_list):
    labels.append('α={}, β={}'.format(a, b))
    y = stats.beta(a=a, b=b).pdf(x)
    plt.axis([0, 1.0, 0, 2.5])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

二项分布

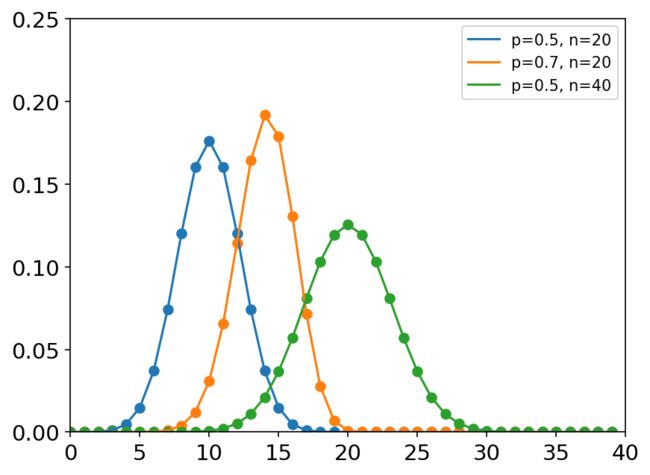
x = np.arange(40)
labels = []
p_list = [0.5, 0.7, 0.5]
n_list = [20, 20, 40]
plt.figure(dpi=150)
for p, n in zip(p_list, n_list):
    labels.append('p={}, n={}'.format(p, n))
    y = stats.binom.pmf(x, n=n, p=p)
    plt.axis([0, 40, 0, 0.25])
    plt.tick_params(axis='both', labelsize=14)
    plt.scatter(x, y)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

卡方分布

x = np.linspace(0, 15, 100)
labels = []
df_list = [1, 2, 4, 6, 11]
plt.figure(dpi=150)
for df in df_list:
    labels.append('df={}'.format(df))
    y = stats.chi2.pdf(x, df)
    plt.axis([0, 14, 0, 0.5])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

狄利克雷分布

from mpl_toolkits.mplot3d import Axes3D

alpha = [1.3, 1.3, 1.3]
s = rng.dirichlet(alpha=alpha, size=1000).transpose()
plt.figure(dpi=150)
ax = plt.gca(projection='3d')
ax.scatter(s[0], s[1], s[2])
ax.view_init(30, 60)  #仰角30°方位角60°
plt.show()

指数分布

x = np.linspace(0, 5, 100)
labels = []
lambda_list = [0.5, 1, 1.5]
plt.figure(dpi=150)
for la in lambda_list:
    labels.append('λ={}'.format(la))
    y = stats.expon.pdf(x, scale=1/la)
    plt.axis([0, 5, 0, 1.5])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

F分布

x = np.linspace(0, 5, 1000)
labels = []
d1_list = [1, 2, 5, 10, 100]
d2_list = [1, 1, 2, 1, 100]
plt.figure(dpi=150)
for d1, d2 in zip(d1_list, d2_list):
    labels.append('d1={}, d2={}'.format(d1, d2))
    y = stats.f.pdf(x, dfn=d1, dfd=d2)
    plt.axis([0, 5, 0, 2.5])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

伽玛分布

x = np.linspace(0, 20, 10000)
labels = []
alpha_list = [1, 2, 3, 5, 9]
beta_list = [2, 2, 2, 1, 0.5]
plt.figure(dpi=150)
for alpha, beta in zip(alpha_list, beta_list):
    labels.append('α={}, β={}'.format(alpha, beta))
    y = stats.gamma.pdf(x, a=alpha, scale=beta)
    plt.axis([0, 20, 0, 0.5])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

几何分布

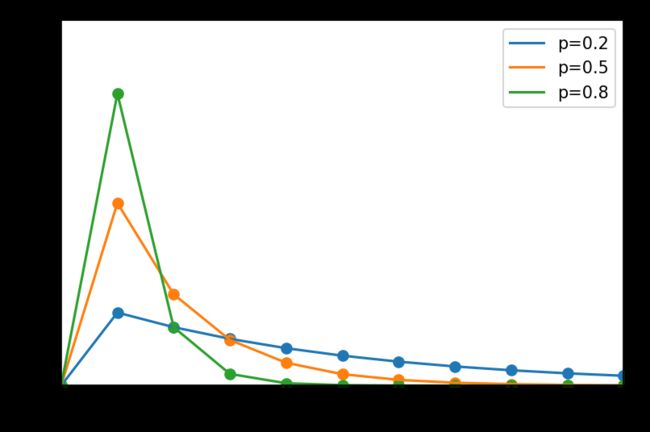
from scipy.interpolate import make_interp_spline

x = np.arange(20)
x_smooth = np.linspace(x.min(), x.max(), 1000)
labels = []
p_list = [0.2, 0.5, 0.8]
plt.figure(dpi=150)
for p in p_list:
    labels.append('p={}'.format(p))
    y = stats.geom.pmf(x, p=p)
    y_smooth = make_interp_spline(x, y)(x_smooth)
    plt.axis([0, 10, 0, 1.0])
    plt.tick_params(axis='both', labelsize=14)
    plt.scatter(x, y)
    plt.plot(x, y)
#     plt.plot(x_smooth, y_smooth)  # 平滑曲线可替换成这句
plt.legend(labels=labels, loc='best')

耿贝尔分布

x = np.linspace(-5, 20, 1000)
labels = []
mu_list = [0.5, 1.0, 1.5, 3.0]
beta_list = [2.0, 2.0, 3.0, 4.0]
plt.figure(dpi=150)
for mu, beta in zip(mu_list, beta_list):
    labels.append('μ={}, β={}'.format(mu, beta))
    y = stats.gumbel_r.pdf(x, loc=mu, scale=beta)
    plt.axis([-5, 20, 0, 0.2])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

超几何分布

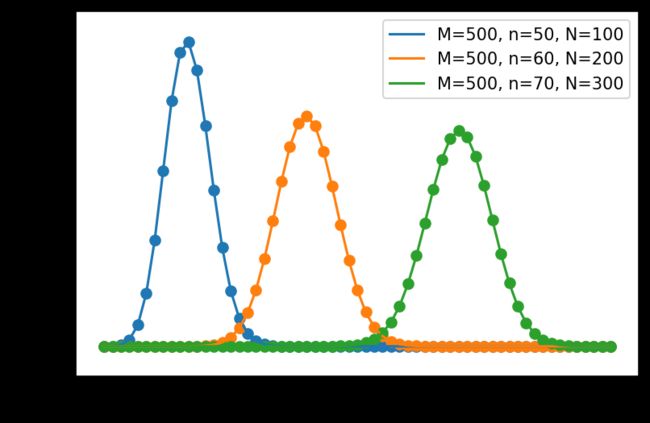
k = np.arange(61)  # 抽到正例数
M = 500  # 正反例总数
n_list = [50, 60, 70]  # 正例总数
N_list = [100, 200, 300]  # 抽样次数

labels = []
plt.figure(dpi=150)
for n, N in zip(n_list, N_list):
    labels.append('M=500, n={}, N={}'.format(n, N))
    y = stats.hypergeom.pmf(k, M, n, N)
    plt.tick_params(axis='both', labelsize=14)
    plt.scatter(k, y)
    plt.plot(k, y)
plt.legend(labels=labels, loc='best')

拉普拉斯分布（双指数分布）

x = np.linspace(-10, 10, 1000)
labels = []
f_list = [stats.norm.pdf, stats.laplace.pdf]
plt.figure(dpi=150)
for f in f_list:
    labels.append(f)
    y = f(x, loc=0, scale=1)
    plt.tick_params(axis='both', labelsize=14)
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.plot(x, y)
plt.legend(labels=['正态分布', '拉普拉斯分布'], loc='best')
plt.rcdefaults() # 重置默认样式

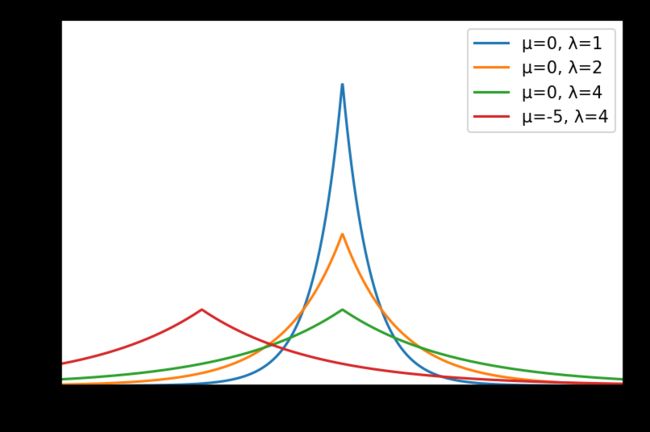
x = np.linspace(-10, 10, 1000)
labels = []
mu_list = [0, 0, 0, -5]
lambda_list = [1, 2, 4, 4]
plt.figure(dpi=150)
for mu, la in zip(mu_list, lambda_list):
    labels.append('μ={}, λ={}'.format(mu, la))
    y = stats.laplace.pdf(x, loc=mu, scale=la)
    plt.axis([-10, 10, 0, 0.6])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

逻辑斯谛分布

x = np.linspace(-5, 20, 1000)
labels = []
mu_list = [5, 9, 9, 6,2]
s_list = [2, 3, 4, 2,1]
plt.figure(dpi=150)
for mu, s in zip(mu_list, s_list):
    labels.append('μ={}, s={}'.format(mu, s))
    y = stats.logistic.pdf(x, loc=mu, scale=s)
    plt.axis([-5, 20, 0, 0.3])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

正态分布

import math

x = np.linspace(-5, 5, 1000)
labels = []
mu_list = [0, 0, 0, -2]
sigma_list = [0.2, 1.0, 5.0, 0.5]
plt.figure(dpi=150)
for mu, sigma in zip(mu_list, sigma_list):
    labels.append('μ={}, σ²={}'.format(mu, sigma))
    y = stats.norm.pdf(x, loc=mu, scale=math.sqrt(sigma))
    plt.axis([-5, 5, 0, 1.0])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

对数正态分布

x = np.linspace(0, 2.5, 1000)
labels = []
mu_list = [0,0,0]
sigma_list = [0.25, 0.5, 1]
plt.figure(dpi=150)
for mu, sigma in zip(mu_list, sigma_list):
    labels.append('μ={}, σ={}'.format(mu, sigma))
    y = stats.lognorm.pdf(x, s=sigma, loc=mu)
    plt.axis([0, 2.5, 0, 2.0])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

对数分布

x = np.arange(1, 6)
labels = []
p_list = [0.33, 0.66, 0.99]
plt.figure(dpi=150)
for p in p_list:
    labels.append('p={}'.format(p))
    y = stats.logser.pmf(x, p=p)
    plt.axis([0, 5, 0, 1.0])
    plt.tick_params(axis='both', labelsize=14)
    plt.scatter(x, y)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

多项分布

参考Multinomial probability density function

多元正态分布

x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
x, y = np.meshgrid(x, y)
pos = np.dstack((x, y))
z = stats.multivariate_normal.pdf(pos, mean=[1, 2], cov=[[3, 0], [0, 15]])
plt.figure(dpi=150)
plt.contourf(x, y, z)

from mpl_toolkits import mplot3d

x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)
pos = np.empty(X.shape + (2, ))
pos[:, :, 0] = X
pos[:, :, 1] = Y
Z = stats.multivariate_normal.pdf(pos, mean=[1, 2], cov=[[3, 0], [0, 15]])
plt.figure(dpi=150)
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis', linewidth=0)

负二项分布

x = np.arange(100)
labels = []
p_list = [0.25, 0.5, 0.75]
n_list = [20, 20, 20]
plt.figure(dpi=150)
for p, n in zip(p_list, n_list):
    labels.append('p={}, n={}'.format(p, n))
    y = stats.nbinom.pmf(x, n=n, p=p)
    plt.axis([0, 100, 0, 0.15])
    plt.tick_params(axis='both', labelsize=14)
    plt.scatter(x, y)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

非中心卡方分布

x = np.linspace(0, 10, 1000)
labels = []
df_list = [2, 2, 2, 4, 4, 4]
lambda_list = [1, 2, 3, 1, 2, 3]
plt.figure(dpi=150)
for df, la in zip(df_list, lambda_list):
    labels.append('df={}, λ={}'.format(df, la))
    y = stats.ncx2.pdf(x, df=df, nc=la)
    plt.axis([0, 10, 0, 0.3])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

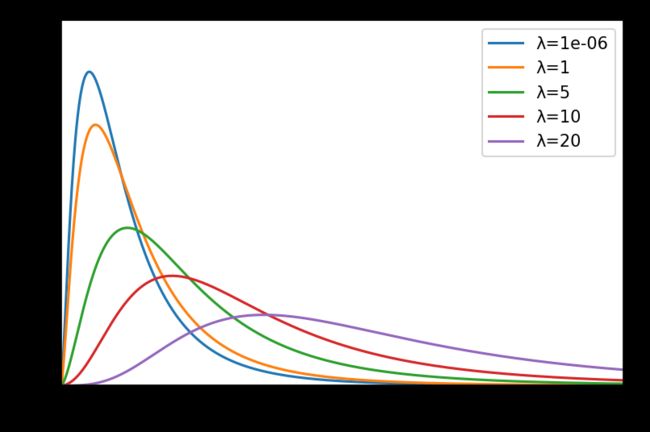
非中心F分布

x = np.linspace(0, 10, 1000)
labels = []
df_list = [5, 10]
lambda_list = [0.000001, 1, 5, 10, 20]  # λ为0时则为F分布
plt.figure(dpi=150)
for la in lambda_list:
    labels.append('λ={}'.format(la))
    y = stats.ncf.pdf(x, dfn=5, dfd=10, nc=la)  # 分子自由度和分母自由度分别为5、10
    plt.axis([0, 10, 0, 0.8])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

帕累托分布II型（Lomax Distribution）

x = np.linspace(0, 6, 1000)
labels = []
lambda_list = [1, 2, 4, 6]
alpha_list = [2, 2, 1, 1]
plt.figure(dpi=150)
for la, alpha in zip(lambda_list, alpha_list):
    labels.append('λ={}, α={}'.format(la, alpha))
    y = stats.lomax.pdf(x, c=alpha, scale=la)
    plt.axis([0, 6, 0, 2])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

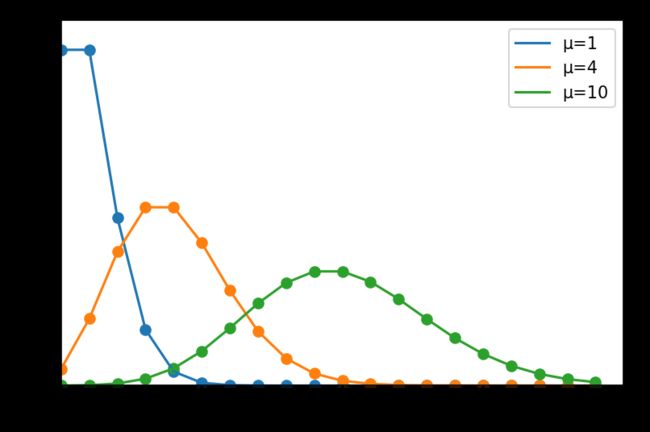
泊松分布

x = np.arange(20)
labels = []
mu_list = [1, 4, 10]
plt.figure(dpi=150)
for mu in mu_list:
    labels.append('μ={}'.format(mu))
    y = stats.poisson.pmf(x, mu=mu)
    plt.axis([0, 20, 0, 0.4])
    plt.tick_params(axis='both', labelsize=14)
    plt.scatter(x, y)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

幂律分布

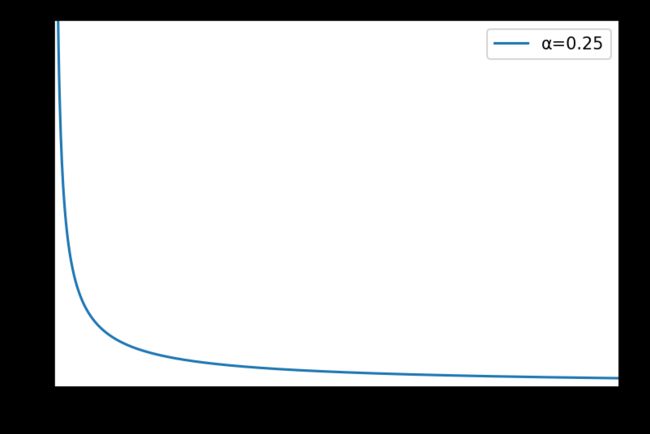
x = np.linspace(0, 1, 1000)
labels = []
plt.figure(dpi=150)
alpha = 2/8  # 28法则
labels.append('α={}'.format(alpha))
y = stats.powerlaw.pdf(x, a=alpha)
plt.axis([0, 1, 0, 10])
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)
plt.legend(labels=labels, loc='best')

瑞利分布

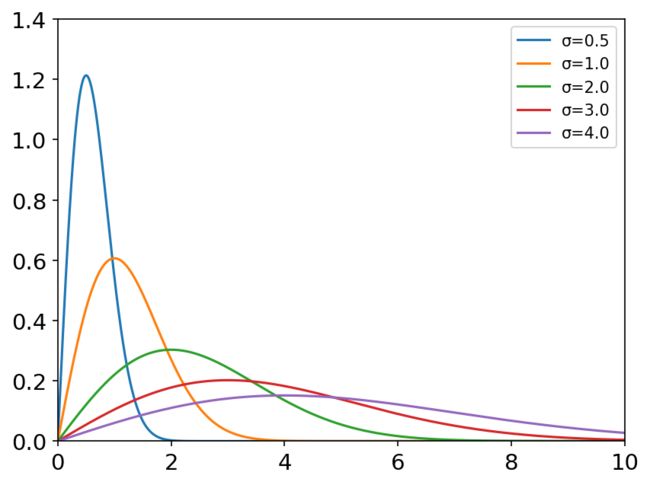
x = np.linspace(0, 10, 1000)
labels = []
sigma_list = [0.5, 1.0, 2.0, 3.0, 4.0]
plt.figure(dpi=150)
for sigma in sigma_list:
    labels.append('σ={}'.format(sigma))
    y = stats.rayleigh.pdf(x, scale=sigma)
    plt.axis([0, 10, 0, 1.4])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

柯西分布（洛伦兹分布）

x = np.linspace(-5, 5, 1000)
labels = []
x0_list = [0, 0, 0, -2]
gamma_list = [0.5, 1.0, 2.0, 1.0]
plt.figure(dpi=150)
for x0, gamma in zip(x0_list, gamma_list):
    labels.append('$x_0$={}, $\gamma$={}'.format(x0, gamma))
    y = stats.cauchy.pdf(x, loc=x0, scale=gamma)
    plt.axis([-5, 5, 0, 0.7])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

标准指数分布

x = np.linspace(0, 5, 100)
la = 1
y = stats.expon.pdf(x, scale=la)
plt.figure(dpi=150)
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)
plt.legend(labels=['λ=1'], loc='best')

标准伽马分布

x = np.linspace(0, 20, 1000)
y = stats.gamma.pdf(x, a=5, scale=1)
plt.figure(dpi=150)
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)
plt.legend(labels=['α=5, β=1'], loc='best')

标准正态分布

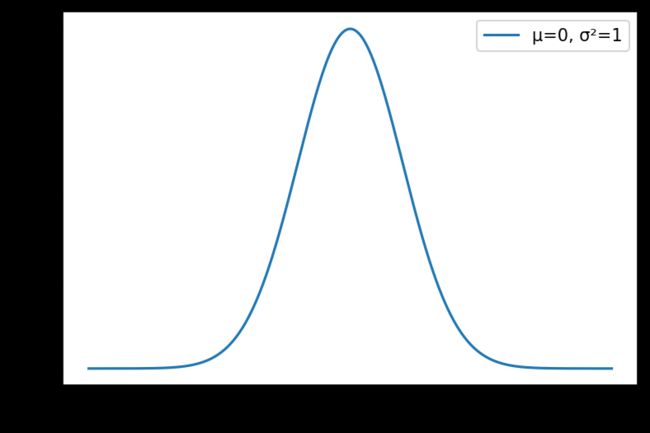
x = np.linspace(-5, 5, 1000)
y = stats.norm.pdf(x, loc=0, scale=1)
plt.figure(dpi=150)
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)
plt.legend(labels=['μ=0, σ²=1'], loc='best')

学生t分布

x = np.linspace(-5, 5, 1000)
labels = []
df_list = [1, 2, 5, 999999]
plt.figure(dpi=150)
for df in df_list:
    labels.append('df={}'.format(df))
    y = stats.t.pdf(x, df=df)
    plt.axis([-5, 5, 0, 0.4])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
labels[-1] = 'df=+∞'
plt.legend(labels=labels, loc='best')

三角形分布

x = np.linspace(-3, 8, 1000)
plt.figure(dpi=150)
left, mode, right = -3, 0, 8  # 三角分布的下限、峰值、上限
y = stats.triang.pdf(x, c=(mode-left)/(right-left), loc=left, scale=right-left)
plt.axis([-3, 8, 0, 0.2])
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)

均匀分布

x = np.linspace(0, 3, 1000)
plt.figure(dpi=150)
a = 1
b = 2
y = stats.uniform.pdf(x, loc=a, scale=b-a)
plt.tick_params(axis='both', labelsize=14)
plt.plot(x, y)

冯·米塞斯分布（循环正态分布）

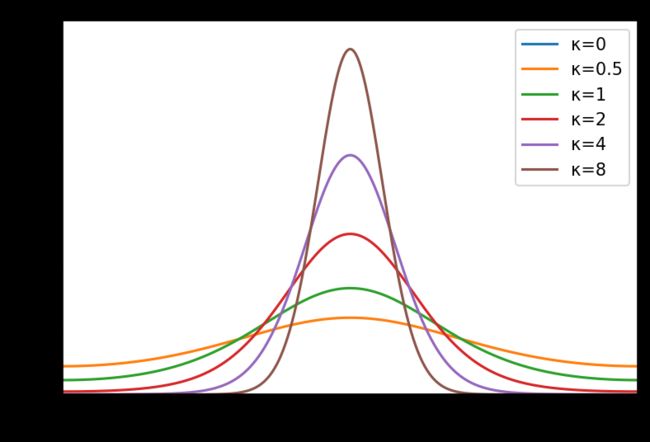
import math

x = np.linspace(-math.pi, math.pi, 1000)
labels = []
kappa_list = [0, 0.5, 1, 2, 4, 8]
plt.figure(dpi=150)
for kappa in kappa_list:
    labels.append('κ={}'.format(kappa))
    y = stats.vonmises.pdf(x, kappa=kappa)
    plt.axis([-math.pi, math.pi, 0, 1.2])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

逆高斯分布（Wald Distribution）

在这里插入代码片

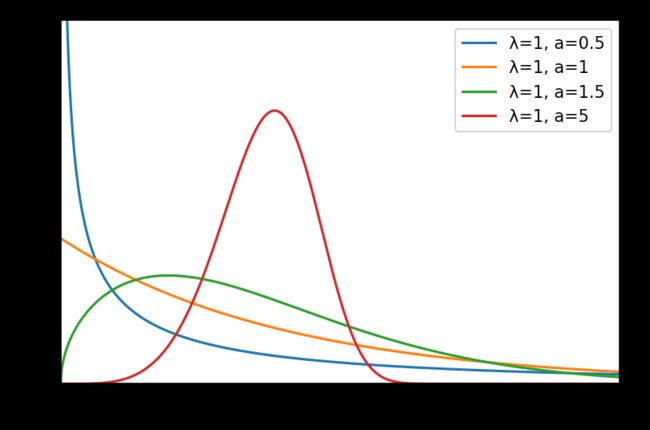
韦伯分布

x = np.linspace(0, 2.5, 1000)
labels = []
lambda_list = [1, 1, 1, 1]
a_list = [0.5, 1, 1.5, 5]
plt.figure(dpi=150)
for la, a in zip(lambda_list, a_list):
    labels.append('λ={}, a={}'.format(la, a))
    y = stats.weibull_min.pdf(x, c=a, scale=la)
    plt.axis([0, 2.5, 0, 2.5])
    plt.tick_params(axis='both', labelsize=14)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')

齐夫分布

x = np.arange(1, 11)
labels = []
a_list = [1, 2, 3, 4]
plt.figure(dpi=150)
ax = plt.gca(xscale='log', yscale='log') # 坐标轴为幂形式
for a in a_list:
    labels.append('a={}'.format(a))
    y = stats.zipf.pmf(k=x, a=a)
    plt.axis([1, 10, 10e-4, 1])
    plt.xticks(np.arange(1, 11), np.arange(1, 11))
    plt.tick_params(axis='both', labelsize=14)
    plt.scatter(x, y)
    plt.plot(x, y)
plt.legend(labels=labels, loc='best')