机器学习系列(5)_从白富美相亲看特征选择与预处理(上)
作者:龙心尘 &&寒小阳
时间:2016年1月。
出处:
http://blog.csdn.net/longxinchen_ml/article/details/50471682
http://blog.csdn.net/han_xiaoyang/article/details/50481967
声明:版权所有,转载请联系作者并注明出处
##1. 引言
再过一个月就是春节,相信有很多码农就要准备欢天喜地地回家过(xiang)年(qin)了。我们今天也打算讲一个相亲的故事。
讲机器学习为什么要讲相亲?被讨论群里的小伙伴催着相亲,哦不,催着讲特征工程紧啊。只是我们不太敢讲这么复杂高深的东西,毕竟工程实践的经验太复杂了,没有统一的好解释的理论,一般的教材讲这方面的内容不多。我们就打算以一个相亲的故事为例,串一些特征工程的内容。
##2. 故事背景
事先声明:本故事纯属虚构,如有雷同,纯属巧合!
海归白富美韩梅梅刚回国,还没适应工作,母亲就催着相亲。以父母的关系,他们了解到的适龄单身男青年有100个。要从100个男生中找到1个理想的女婿,可谓百里挑一。韩梅梅母亲也担心女儿相亲多了会反感,打算草拟一个相亲名单,人数不多。怎么从中挑出优秀男青年就是一个首要的问题。
##3. 用机器学习的框架去分析
我们用机器学习的框架分析,在父母眼中,这100个男生最终将会分成两类:“女婿”(1人)和“非女婿”(99人)。“女婿”和“非女婿”就叫做“标签”。
而选择相亲名单的标准——如“是否高富帅”、“是否海归”等等——就叫作“特征”。最好能有一个特征能够精确定位理想女婿。但这太过理想了。比较现实的方法是从这些“特征”中选择、拆分、组合出最合适的特征,逐渐逼近我们的标签,以形成一个精简的相亲名单。而这个过程,就可以理解成特征处理、特征工程的过程。
但是,**现实中的特征有千千万,拆分重组之后特征又是几何级数地增加,可能永远也穷举不完。因此需要有统一客观的指标来衡量这些特征对标签的识别能力,以便进一步地深入分析。**而评估这些“特征”对我们的“标签”的有效程度的过程就叫作“特征有效性分析”。
##4. 剧情一:韩妈妈的“如意算盘”
为人父母嘛,总是希望女儿嫁得好。韩妈妈的第一反应的就是要找“高富帅”。先她先从这100个男生中挑了挑,符合高富帅这个标准的有5个人。
韩妈妈的如意算盘是这样的:女婿就从这5个人中挑,概率就是20%,比之前的1%整整提高了20倍,嘿嘿嘿。。。
##5. 特征有效性分析
其实,这就韩妈妈不知不觉就走了一个特征有效性分析的过程。我们用图表演示一下:
> 只是在工程上做除法可能运算会麻烦些,而两边同时取对数转换成减法则更方便:$\frac{后验概率}{先验概率}=\frac{20\%}{1\%}=20(倍)$。
$log(\frac{后验概率}{先验概率})=log(后验概率)-log(先验概率) $ **概率表示着选女婿的可能性或者确定性。在本例中,后验概率的确定性比先验概率的确定性更高。**可见,“确定性的增加”可以作为特征有效性分析的一个指标。
我们进一步分析,无论先验概率还是后验概率,其本身是0-1之间的一个数,取完对数之后是一个负数,这在现实中不太方便找到其对应的现象解释。但是概率的倒数一定大于1,取完对数之后就是一个正数,就好找现实解释了。我们可以把这个**“概率倒数的对数”理解成不确定性的指标。**于是上式就变成:
$log(\frac{后验概率}{先验概率})=log(\frac{1}{先验概率})-log(\frac{1}{后验概率})$ 这里面的** l o g ( 后 验 概 率 先 验 概 率 ) log(\frac{后验概率}{先验概率}) log(先验概率后验概率)我们叫做互信息**。
因此,“不确定性的减少”可以作为特征有效性分析的一个指标。这个结论我们接下来将会反复用到。
##6. 剧情二:白富美巧劝慈母
韩妈妈半开玩笑地问韩梅梅:“我们家闺女只挑高富帅的怎么样?”女儿想了想,说:“如果人家看不上我们怎么办?”母亲笑着说:“我们的家境哪里差了?何况我们的女儿这么优秀,我们还看不上他们呢。”
女儿说:“这就是说明我们双方不合适了。我们家条件虽然还不错,但是比下有余、比上不足,跟真正条件好的家庭比较起来我们根本不算事儿。如果一味挑高富帅,他们可能觉得我们只是看中他们的钱,反倒把我们家看低了。相反,要是真要有个真正对我好的男生,比什么都幸福,而他不一定必须是高富帅。毕竟跟我一起相处一辈子的是一个活生生的人,而不是他背后的东西嘛。”
母亲很有感慨地说:“嗯,你能这样想我就放心了。梅梅真是长大了。那么,你打算怎么办?”女儿说道:“高富帅也得分人,踏实人品好的也可以接触一下,但是玩心太重不会照顾人的我就不喜欢。估计高富帅里面这两种人一半一半吧。很多男生并不是高富帅,其中没准也有合适的人呢。”
##7. 特征有效性分析
现在特征的分布发生了新变化。按韩梅梅的分析,高富帅中可能有一半她就不会喜欢,而不是高富帅的男生中没准有合适的人。我们可以简单假设高富帅中与非高富帅中各有0.5个合适的人。则分析图表如下:

现在的情况是,**“是不是女婿”的可能性同时分布在“是高富帅”和“不是高富帅”中,**单独衡量“高富帅”本身的后验概率已经不够描述特征的整体效果了。我们可以有一个考虑特征整体情况的指标。
还是回到之前的那句话:
“不确定性的减少”可以作为特征有效性分析的一个指标。
我们之前考虑了“是女婿”的不确定性是 l o g ( 1 1 % ) log(\frac{1}{1\%}) log(1%1),相应的“不是女婿”的不确定性是 l o g ( 1 99 % ) log(\frac{1}{99\%}) log(99%1),那么标签“是否女婿”作为整体的平均不确定性则可以理解为这两个状态的加权平均:
H ( Y ) = 1 % × l o g ( 1 1 % ) + 99 % × l o g ( 1 99 % ) = 0.08079 H(Y)=1\%×log(\frac{1}{1\%})+99\%×log(\frac{1}{99\%})=0.08079 H(Y)=1%×log(1%1)+99%×log(99%1)=0.08079。(全文假定对数log的底数取为2)
这就是传说中的信息熵。我们用Y表示标签,用 H ( Y ) H(Y) H(Y)表示“是否女婿”的信息熵,也就是其整体的平均不确定性。
那么考虑特征(“是否高帅富”)后的标签(“是否女婿”)的平均不确定性怎么衡量?我们用 X : { “ 是 高 富 帅 ” , “ 不 是 高 富 帅 ” } X:\{“是高富帅”,“不是高富帅”\} X:{“是高富帅”,“不是高富帅”}来表示特征。其实,与上面的思路类似,我们在已知特征为“是高富帅”的前提下,“是否女婿”这个标签的整体平均不确定性可以用相对“是高富帅”的后验概率来求出:
H ( Y ∣ X = “ 是 高 富 帅 ” ) = ( 0.5 / 5 ) × l o g ( 1 ( 0.5 / 5 ) ) + ( 4.5 / 5 ) × l o g ( 1 ( 4.5 / 5 ) ) = 0.46900 H(Y|X=“是高富帅”) = (0.5/5)×log(\frac{1}{(0.5/5)})+(4.5/5)×log(\frac{1}{(4.5/5)}) = 0.46900 H(Y∣X=“是高富帅”)=(0.5/5)×log((0.5/5)1)+(4.5/5)×log((4.5/5)1)=0.46900
在已知特征为“不是高富帅”的前提下,“是否女婿”这个标签的整体平均不确定性可以用相对“不是高富帅”的后验概率来求出:
H ( Y ∣ X = “ 不 是 高 富 帅 ” ) = ( 0.5 / 95 ) × l o g ( 1 ( 0.5 / 95 ) ) + ( 94.5 / 95 ) × l o g ( 1 ( 94.5 / 95 ) ) = 0.04741 H(Y|X=“不是高富帅”) = (0.5/95)×log(\frac{1}{(0.5/95)})+(94.5/95)×log(\frac{1}{(94.5/95)}) = 0.04741 H(Y∣X=“不是高富帅”)=(0.5/95)×log((0.5/95)1)+(94.5/95)×log((94.5/95)1)=0.04741。
因此,已知特征(无论具体是“是高富帅”还是“不是高富帅”)情况下的标签平均不确定性为前面两种情况的加权平均:
H ( Y ∣ X ) H(Y|X) H(Y∣X)
= P ( X = “ 是 高 富 帅 ” ) × H ( Y ∣ X = “ 是 高 富 帅 ” ) + P ( X = “ 不 是 高 富 帅 ” ) × H ( Y ∣ X = “ 不 是 高 富 帅 ” ) =P(X=“是高富帅”)×H(Y|X=“是高富帅”)+P(X=“不是高富帅”)×H(Y|X=“不是高富帅”) =P(X=“是高富帅”)×H(Y∣X=“是高富帅”)+P(X=“不是高富帅”)×H(Y∣X=“不是高富帅”)
= 5 / 100 × 0.46900 + 95 / 100 × 0.04741 = 0.06849 =5/100×0.46900+95/100×0.04741=0.06849 =5/100×0.46900+95/100×0.04741=0.06849
这就是传说中的条件熵。
所以,**考虑特征后,标签的“不确定性的减少”**为:
$ I(Y,X)=H(Y)- H(Y|X)=0.01230 $
这个 I ( Y , X ) I(Y,X) I(Y,X)就叫做平均互信息。
我们用同样的方法去评价之前母亲设想的女婿只在高富帅中的理想情况(也就是女婿只在高富帅中产生的情况)的互信息 I ( Y , X ’ ) = 0.04470 I(Y,X’)=0.04470 I(Y,X’)=0.04470
平均互信息**从理想情况的0.04470下降到0.01230,也就是说原以为特征“是否高富帅”与标签“是否女婿”的相关性很高,后来发现相关性其实是比较低的。**可见理想很丰满,现实很骨感。
##8. 剧情三:白富美重定名单
其实,韩梅梅没有说出来的话是她有一个青梅竹马的码农叫李雷。她出国之前的对他的印象还不错。如果按母亲的标准李雷肯定排除在相亲名单外了,而她想给他一个机会。
这时母亲说话了:“我们家女儿考虑得挺好,那相亲名单你来定吧。”女儿说:“不是高富帅的男生也该好好区分一下,那些品行端正、气度不凡、踏实肯干的潜力股的男生我也比较欣赏,其他的就暂且不考虑了。”母亲说:“就是说可以从高富帅中挑出部分品德好的,还有从不是高帅富的男生中挑出部分潜力股,共同组成一个新的名单,我们的女婿就在这里面了?”女儿不好意思地说:“妈妈您真着急,八字还没一撇呢。”
接着,韩梅梅母女俩从高富帅中挑了2个口碑不错的,又从不是高富帅的男生中条了10个很不错的。最终组成了12人的相亲名单。李雷的名字在其中。
##9. 拆分重组成为新特征
其实以上韩梅梅母女俩完成了一次特征的拆分与重组过程。具体图示如下:
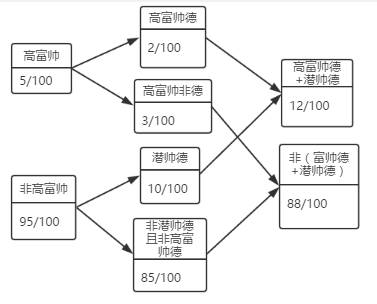
这里用“潜帅德”表示韩梅梅对“品行端正、气度不凡、踏实肯干的潜力股”的特征的描述。
特征进行拆分与重组的过程在特征工程中经常出现。因为当你对特征与标签的相关性有定量的评估方法后,会筛选出那些不那么显著的特征(如本例中的“是否高富帅”),然后去分析考核指标这么低的原因,启发你引入新的特征(如本例中的“是否品德良好”、“是否有潜力”)将原有特征拆分重组,可能会有更好的效果。而这些生成的新特征,又要经过特征有效性分析来最终评估。如此反复迭代。
我们用 X 2 X_2 X2来表示新特征,与上面的思路类似,我们计算 X 2 X_2 X2的平均互信息:
$ I(Y,X_2)=H(Y)- H(Y|X_2)= 0.03114$
与之前的平均互信息 I ( Y , X ) = 0.01230 I(Y,X)=0.01230 I(Y,X)=0.01230比起来,有了显著提高。可见新特征 X 2 X_2 X2比之前的特征 X X X更有效。
##11. 剧情四:韩妈妈给名单分级
在跟韩梅梅聊完之后,韩妈妈转念一想:“为什么非要有一份相亲名单?可以把这12个人再分成两类,第一类是高富帅的,先相亲。这些觉得不合适后再考虑剩下的10个人啊。”
我们继续分析,用 X 3 X_3 X3来表示新特征,与上面的思路类似,我们计算 X 3 X_3 X3的平均互信息:
$I(Y,X_3)=H(Y)- H(Y|X_3)= 0.03593$
与之前的平均互信息 I ( Y , X 2 ) = 0.03114 I(Y,X_2)=0.03114 I(Y,X2)=0.03114比起来,又有了一定的提高。可见新特征 X 3 X_3 X3比之前的特征 X 2 X_2 X2更有效。
韩妈妈真是为女儿的相亲操碎了心。
##13. 剧情五:韩妈妈问计赵媒婆
韩妈妈思索完之后抑制不住内心的兴奋,想找人倾诉。这时她正好在路上碰见了赵媒婆。赵媒婆在韩妈妈的老闺蜜圈中享有盛誉,相亲非常有经验。
赵媒婆听了韩妈妈的诉说后,微微一笑,说:“你这个名单不够专业。”韩妈妈大为诧异。赵媒婆继续说:“高、富、帅三个特征本来就是相互独立的三个特征,你硬生生地绑在一起,多少大好青年被你给甩掉了。后面的潜力股啊、人品端正啊什么的都类似。”韩妈妈恍然大悟:“真是这样啊。”
赵媒婆说:“其实你这里最大的问题是这些特征的评估都是拍脑袋决定,没有充分的现实数据做支撑,很可能会犯错误的。”韩妈妈暗暗点头,心生佩服。
赵媒婆接着说:“还有一个问题,你准备了两份名单,也就是把人群分成了三份,你算平均互信息只能评价整体的,具体到每一份人群你怎么对他们评价?”韩妈妈想了想,说:“我们可以直接用相对于某个具体条件的信息熵啊。”赵媒婆说:“何苦这么麻烦呢?”
韩妈妈听她话里有话,打算继续问下去。
##14. 评价特征选项的两个方法
在赵媒婆最后一个问题中,韩妈妈所说的其实是可以计算以下三个值来评估具体的特征选项:
- H ( Y ∣ X 3 = “ 高 富 帅 德 ” ) H(Y|X_3=“高富帅德”) H(Y∣X3=“高富帅德”)
- H ( Y ∣ X 3 = “ 潜 帅 德 ” ) H(Y|X_3= “潜帅德”) H(Y∣X3=“潜帅德”)
- H ( Y ∣ X 3 = “ 不 是 高 富 帅 德 且 不 是 潜 帅 德 ” ) H(Y|X_3= “不是高富帅德且不是潜帅德”) H(Y∣X3=“不是高富帅德且不是潜帅德”)
而这三个值**在之前计算条件熵 H ( Y ∣ X 3 ) H(Y|X_3) H(Y∣X3)的过程中就已经计算出来了。**所以比较起来应该很方便。
但其实更简单的方法用他们相对于所需要标签的后验概率评价。如下图红色的部分,比较大小就可以找出评价较好的特征。

显然“高富帅德”的评分最高(0.25),“潜帅德”的评分次之(0.05),“不是高富帅德且不是潜帅德”评分最差(0)。符合韩妈妈的预期。
然而,赵媒婆的想说的并不是这种方法,而是逻辑回归……
##15. 剧情六:赵媒婆的数据库
赵媒婆不等韩妈妈说话,就直接拿出了自己的神器:一个平板电脑。然后打开她的相亲数据库,点了点鼠标,一张巨大的表展现出来。韩妈妈目瞪口呆:“现在媒婆都用高科技了?”赵媒婆傲娇地说:“那是。”
这张大表是她这么多年来全国各地相亲介绍的所有男生信息,分别标注了每个男生的升高、年龄、年薪、长相特点、教育经历、工作经历、是否海归、工作年限、工作公司、工作地点、出身地、是否有户口、是否公务员、具体职业、行业、性格倾向等等信息。
她还有一张女生信息表,另外一张男生女生相亲情况表(相亲成功、相亲不成、继续发展、未接触)。媒婆一一给韩妈妈解释这些信息。韩妈妈连连惊呼。
赵媒婆接着说道:“我们可以从里面找出跟你女儿情况相近的一些女生信息,再把跟她们相过亲的男生找出来,把其中相亲成功的归为一类,剩下的归为另一类。然后假设男生的每个特征对相亲成功都有贡献,贡献的权重为 w i w_i wi。我们用逻辑回归的方法可以求出这些权重,把这些权重大的特征挑出来,你再用它们来找女婿就方便了。”
韩妈妈说:“逻辑什么?”赵媒婆说:“高科技了,你不懂的。不过给我干儿子写了个博客来介绍,你可以看看。”
##16. 特征筛选与特征工程工作流
呃,我们什么时候成赵媒婆的干儿子了?先不管这些。逻辑回归并不是什么高科技,在前面的文章里已有简单的解释。我们在这里就补充说明一下为什么可以用权重来衡量特征的贡献。以下是一个典型的逻辑回归过程:

我们期望 P ( z ) P(z) P(z)的概率越大越好, s i g m o i d sigmoid sigmoid函数是个单调递增函数,所以z越大越好,**在所有特征都归一化的前提下,显然是权重 w i w_i wi越大越好。**因此与 w i w_i wi对应的特征就是我们要寻找的显著特征。而那些权重小的特征就可以先不考虑了。这就完成了一个最简单的特征筛选的过程。
当然,这里所说的权重大可以指的是权重的绝对值很大,比如特征“富”的权重是-100,是一个很小的数,但这也就意味着“不富”的权重会很大,以至于显著影响我们的z的结果。所以这也是一个显著特征。
需要补充一下的是,在工程实践中,权重的幅度和正则化也有关系。L1正则化会把特征拉稀疏,会产出一部分0特征。而不是0的那些特征,是有作用的特征。所以L1正则化其实具备一定的特征选择(feature selection)的作用。尤其是很高维空间的feature,用L1正则化,其实能帮助做一下feature selection的。而L2正则化,则会把各个维度的权重拉平均一些,抑制住各个维度权重幅度的方差。但是抑制归抑制,最后的权重还是会有大小差异,就像上文说的,绝对值大的权重,对应的特征区分度好一些。
对于那些不够显著的特征,我们需要分析一下这个特征的具体情况是怎样,**是否需要对其进行重新拆分与重组,拆分重组后新的特征又可以进行特征有效性分析。如此不断迭代反复,**就可以挑选出比较理想的特征了。
我们用以下整个工作流大致展现这个过程。由于很多内容没有展开,我们先把名字写进去,在后续的文章中继续扩展。
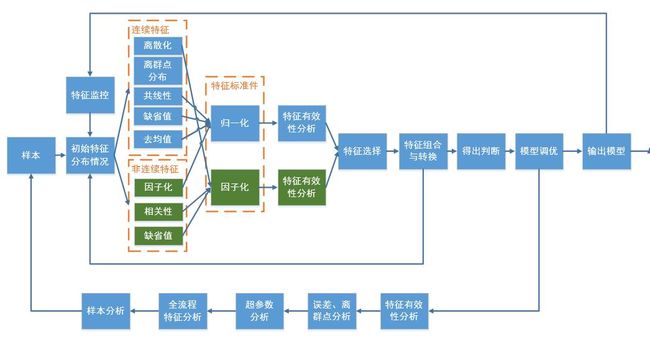
##17. 剧情七:韩妈妈新名单尘埃落定
在韩妈妈与赵媒婆的尽心鼓捣下,最终生成了一个只有4个人的相亲名单。其中只剩下一名高富帅,另外三人中有一人正是李雷。韩妈妈拿着新名单给女儿看,韩梅梅沉默半晌,心想李雷在四人名单中怎么也能存在,莫非这也是缘分?
##18. 小结
本文中主要讲了一些特征有效性分析的方法,包括用互信息,平均互信息,条件熵,后验概率,逻辑回归权重等方法对特征与标签的相关性进行了评估。有了这些评估做基础,可以筛选出显著的特征,并对对不显著的特征进行分析、拆分和重组,最终形成新的特征并反复迭代。本文略过了一些特征预处理的方法,并对特征有效性评估的阐述不够充分,我们将在接下来的文章中予以讨论。

