opencv-python +ski-image实现指静脉的LBP（局部二进制模式）特征提取

LBP：

我对original LBP的理解是：对一个灰度图像的每个像素，用这个像素周围一格或者N格的其他像素做比较，最后将这周围（一般是8个）得到的比较结果串起来得到一个8位二进制的串，用这个8位二进制数在一个同等大小的矩阵中的同等位置替代原来像素信息，遍历整个图像即可得到这副图像的LBP图像。原理上来说，original LBP 具有灰度不变性。而如果用一个圆形的8个（或者更多）等分点来代替原来的矩形，并且将最后得到8位二进制的串进行移位，使得最后的串值最小，这样的LBP就具有了旋转不变性。

 

当然LBP 还有其他的形式，点击这里你的雷哥的博客可以帮助了解。

网上很多博客都介绍了如何实现LBP的提取，但是我有点累。。。不想造轮子了。

于是推荐大家使用 ski-image，这个包里对各种LBP的方法有一个很友好的封装。

ski-image官方文档

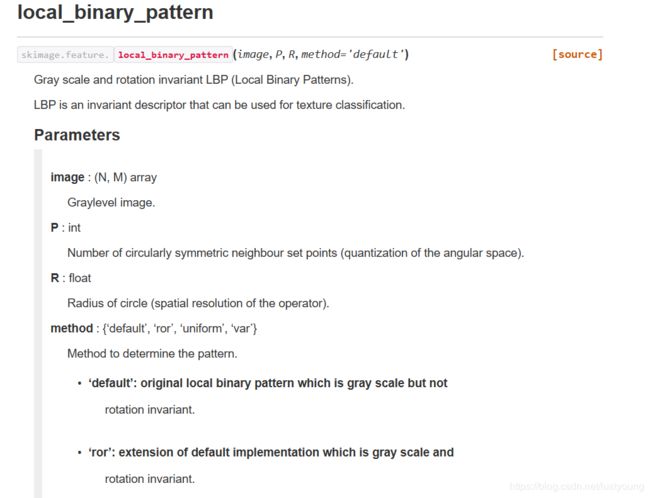
下面是有关这个函数local_binary_pattern的截图

里面对几种LBP方法都做了介绍。这里我使用的original LBP， 就是上面的default方法。

 

实践：

过程：得到LBP图像-》分块-》对每块统计LBP直方图-》对所有直方图做归一化处理-》串接所有直方图得到LBP特征向量

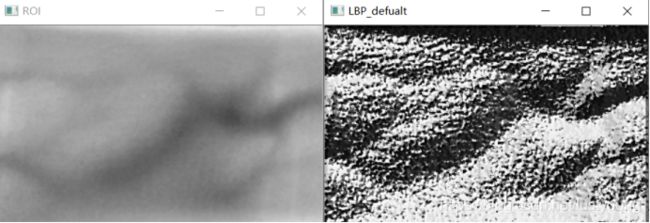
以下代码可以很快的得到一副二值图像的LBP编码图。彩色图像是不行的，会报错：ValueError: The parameter `image` must be a 2-dimensional array

from skimage import feature

dst1=feature.local_binary_pattern(roi,8,3,'default')

这里的dst1中的数据类型是float64，我为了使用opencv中的统计直方图的函数，将dst1转换为了uint8

dst1=feature.local_binary_pattern(roi,8,3,'default')
dst2=feature.local_binary_pattern(roi,8,1,'uniform')
dst3=feature.local_binary_pattern(roi,8,3,'ror')

dst1=dst1.astype('uint8')  #转换数据类型，便于后面处理

 

 转化后可以用imshow看到转化后的图片

（有一种毛玻璃的感觉  ：p）

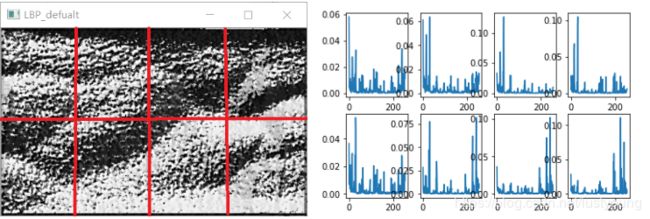
下一步是分块，统计直方图，分别归一化最后拼接

分块：直接用基本的ROI提取每一块

统计直方图：我用的是cv2中有的hist=cv.calcHist([tile],[0],None,[255],[0,255])，

归一化：这个值的数量（轴高度）/所有高度相加  得到的小数代替原来的值

拼接：串联~~~

我将完成这些任务的功能都写在了函数LBP_hist中。（详见附件LBP_feature.py）

LBP_hist(path='0',ROI_img=None)，此函数接收一个ROI图像的文件或者ROI图像，最后返回归一化并且拼接好的特征向量。

这里贴一下代码：

def LBP_hist(path='0',ROI_img=None):  #path : a path of roi  img : a  ROI img  
    if path!='0':
        img1=cv.imread(path,0)
    else:
        img1=cv.cvtColor(ROI_img,cv.COLOR_BGR2GRAY)
    img=feature.local_binary_pattern(img1,8,3,'default')
    img=img.astype('uint8')
    tile_cols=4
    tile_rows=2
    n=1
    rows,cols=img.shape
    step_rows=round(rows/tile_rows)-1
    step_cols=round(cols/tile_cols)-1
    feature1=[]
    for i in range(tile_rows):
        for j in range(tile_cols):
            tile=img[i*step_rows:(i+1)*step_rows-1,j*step_cols:(j+1)*step_cols-1]
            hist=cv.calcHist([tile],[0],None,[255],[0,255])
            hist=normalization(hist)
            feature1.append(hist) 
            plt.subplot(240+n)
            plt.plot(hist)
            n+=1
    plt.show()
    feature1=np.array(feature1)
    feature1=feature1.ravel()
    return feature1

def normalization(array) : #array 为nparry
    array=array.ravel()
    result =[]
    array_sum=array.sum()
    for i in array:
        result.append(i/array_sum)
    return np.array(result)

源文件可以去我的github下载

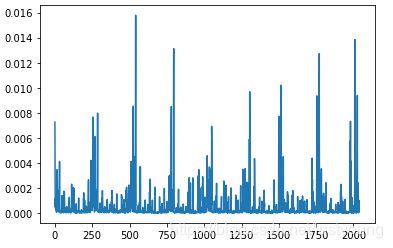
这是最后得到的LBP特征：

 

点个赞噢亲~