电信行业用户流失预测——你的用户会流失吗？

博客目的

随着通信技术的飞速发展，通信用户数量的急剧增加，通信市场趋于饱和，运营商之间的竞争愈演愈烈，使得运营商更加关注用户资源流失的问题。通过使用用户产生的数据预测潜在的流失用户，并对这些潜在的流失用户进行挽留，可以保持市场占比和利润。所以用户流失预测问题的研究对于电信行业而言有着重要的意义。
本文从特征和流失的关联性和逻辑回归模型两个方面来对电信用户流失预测问题进行分析研究，主要解决两个问题，一是什么样的用户容易流失，二是用户会不会流失。针对以上两个问题分别给出容易流失的用户画像和用户流失模型。

关键词： 用户流失 预测 逻辑回归 机器学习

一、加载数据

数据来源有：
1、kaggle
2、百度网盘链接：https://pan.baidu.com/s/1APmQrOz2mTCislWqUiFSdA
提取码：6ice

开发环境介绍：
编程语言：python，编程工具：Jupyter notebook，常用库：pandas、numpy、sklearn。

首先加载文件，接着观察特征有无缺失值，特征数据类型符合不符合认知等，为数据预处理做准备，然后对特征进行分类方便后期分组研究特征和流失的关联性。

df_ = pd.read_csv("WA_Fn-UseC_-Telco-Customer-Churn.csv")
df = df_.copy()

# 看下数据类型
df.info()

RangeIndex: 7043 entries, 0 to 7042
Data columns (total 21 columns):
 #   Column            Non-Null Count  Dtype  
---  ------            --------------  -----  
 0   customerID        7043 non-null   object 
 1   gender            7043 non-null   object 
 2   SeniorCitizen     7043 non-null   int64  
 3   Partner           7043 non-null   object 
 4   Dependents        7043 non-null   object 
 5   tenure            7043 non-null   int64  
 6   PhoneService      7043 non-null   object 
 7   MultipleLines     7043 non-null   object 
 8   InternetService   7043 non-null   object 
 9   OnlineSecurity    7043 non-null   object 
 10  OnlineBackup      7043 non-null   object 
 11  DeviceProtection  7043 non-null   object 
 12  TechSupport       7043 non-null   object 
 13  StreamingTV       7043 non-null   object 
 14  StreamingMovies   7043 non-null   object 
 15  Contract          7043 non-null   object 
 16  PaperlessBilling  7043 non-null   object 
 17  PaymentMethod     7043 non-null   object 
 18  MonthlyCharges    7043 non-null   float64
 19  TotalCharges      7043 non-null   object 
 20  Churn             7043 non-null   object 
dtypes: float64(1), int64(2), object(18)
memory usage: 1.1+ MB

从结果可以看出：一共7043行数据，21个特征，每一列都没有缺失值，但是TotalCharges应该是数值型变量的而不应该是object类型，所以在数据预处理里要对TotalCharges进行转换，转换成数值型变量。
大多数模型都不能直接处理string数据只能处理数值数据，观察离散变量的属性值能帮助我们判断将其转成有序变量还是名义变量。

# 看看离散型变量都有哪些属性值
col_dict = {}
del_col = ["customerID", "tenure", "MonthlyCharges", "TotalCharges"]
for i in [x for x in df.columns.tolist() if x not in del_col]:
    col_dict[i] = df[i].unique().tolist()
col_dict

{'gender': ['Female', 'Male'],
 'SeniorCitizen': [0, 1],
 'Partner': ['Yes', 'No'],
 'Dependents': ['No', 'Yes'],
 'PhoneService': ['No', 'Yes'],
 'MultipleLines': ['No phone service', 'No', 'Yes'],
 'InternetService': ['DSL', 'Fiber optic', 'No'],
 'OnlineSecurity': ['No', 'Yes', 'No internet service'],
 'OnlineBackup': ['Yes', 'No', 'No internet service'],
 'DeviceProtection': ['No', 'Yes', 'No internet service'],
 'TechSupport': ['No', 'Yes', 'No internet service'],
 'StreamingTV': ['No', 'Yes', 'No internet service'],
 'StreamingMovies': ['No', 'Yes', 'No internet service'],
 'Contract': ['Month-to-month', 'One year', 'Two year'],
 'PaperlessBilling': ['Yes', 'No'],
 'PaymentMethod': ['Electronic check',
  'Mailed check',
  'Bank transfer (automatic)',
  'Credit card (automatic)'],
 'Churn': ['No', 'Yes']}

# 看看数值型变量的描述性统计信息
df.describe()

	SeniorCitizen	tenure	MonthlyCharges
count	7043.000000	7043.000000	7043.000000
mean	0.162147	32.371149	64.761692
std	0.368612	24.559481	30.090047
min	0.000000	0.000000	18.250000
25%	0.000000	9.000000	35.500000
50%	0.000000	29.000000	70.350000
75%	0.000000	55.000000	89.850000
max	1.000000	72.000000	118.750000

二、数据预处理

这部分展示数据常规的预处理手段。

2.1 去重复

print("去重前数据大小为：{0}".format(df.shape))
df.drop_duplicates()
print("去重后数据大小为：{0}".format(df.shape))

去重前数据大小为：(7043, 21)
去重后数据大小为：(7043, 21)

从结果可以看出，数据没有重复的。如果有重复数据一定要删除，删除后记得重新设置索引。

2.2 缺失值

df.isnull().sum()

customerID          0
gender              0
SeniorCitizen       0
Partner             0
Dependents          0
tenure              0
PhoneService        0
MultipleLines       0
InternetService     0
OnlineSecurity      0
OnlineBackup        0
DeviceProtection    0
TechSupport         0
StreamingTV         0
StreamingMovies     0
Contract            0
PaperlessBilling    0
PaymentMethod       0
MonthlyCharges      0
TotalCharges        0
Churn               0
dtype: int64

从结果可以看出没有特征含有缺失值。

2.3 TotalCharges特征数值化

df['TotalCharges'] = pd.to_numeric(df["TotalCharges"])

报错：ValueError: Unable to parse string " " at position 488。
从报错信息里可以看出这一列包含空白值，我们看看多不多，多的话用均值或其他的填补，少的话直接删掉。

(df['TotalCharges']==" ").sum()

11

(df['TotalCharges']==" ").sum()/df.shape[0]

0.001561834445548772

从以上2个结果可以看出，TotalCharges列一共有11个空白值" “，占总数据的比例是0.15%，这个比例还是很小的，这11个空白值” "直接删掉，删掉后注意更新下数据的索引。

df.drop(df[df["TotalCharges"]==" "].index, axis=0, inplace=True)
# 重设索引，删除某些行后最好是重设下索引
df.index = range(df.shape[0])
df['TotalCharges'] = pd.to_numeric(df["TotalCharges"])

2.4 异常值

观察分位数和可视化结合，检查连续变量有没有异常值。

range_ = list(np.linspace(0,1,6))
df.describe(percentiles=range_)

	SeniorCitizen	tenure	MonthlyCharges	TotalCharges
count	7032.000000	7032.000000	7032.000000	7032.000000
mean	0.162400	32.421786	64.798208	2283.300441
std	0.368844	24.545260	30.085974	2266.771362
min	0.000000	1.000000	18.250000	18.800000
0%	0.000000	1.000000	18.250000	18.800000
20%	0.000000	6.000000	25.050000	267.070000
40%	0.000000	20.000000	58.920000	944.170000
50%	0.000000	29.000000	70.350000	1397.475000
60%	0.000000	40.000000	79.150000	2048.950000
80%	0.000000	60.800000	94.300000	4475.410000
100%	1.000000	72.000000	118.750000	8684.800000
max	1.000000	72.000000	118.750000	8684.800000

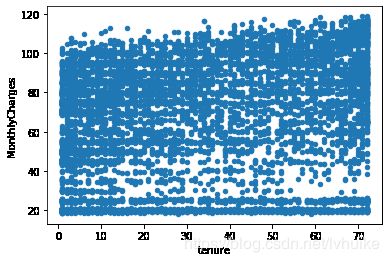
df.plot(kind='scatter', x='tenure', y='MonthlyCharges')

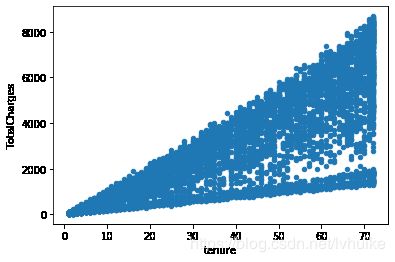
df.plot(kind='scatter', x='tenure', y='TotalCharges')

从分位数和图中可以看出，连续型变量没有很特别的异常值。

2.5 无量纲化——标准化

树模型不需要对数据缩放就能得到较好的准确率，因为我们还要构建其他需要对数据进行缩放的模型，所以才需要对数据做无量纲化。连续型变量尤其是"MonthlyCharges" 和 “TotalCharges”，数值从几十到几千取值范围很大，使用无量纲化可以帮助我们提升某些模型的准确率，避免某些取值范围特别大的特征对模型的影响。
无量纲化通常有两种，归一化和标准化，本文使用更常用的标准化。因为归一化对异常值非常敏感，在PCA，聚类，逻辑回归，支持向量机，神经网络这些算法中，标准化往往是最好的选择。

# 连续变量做无量纲化处理，离散变量不需要
scaler_ = ["tenure", "MonthlyCharges", "TotalCharges"]
df_nor = df.copy()
df_nor[scaler_] = StandardScaler().fit_transform(df_nor[scaler_])

df_nor.head()

	customerID	gender	SeniorCitizen	Partner	Dependents	tenure	PhoneService	MultipleLines	InternetService	OnlineSecurity	...	DeviceProtection	TechSupport	StreamingTV	StreamingMovies	Contract	PaperlessBilling	PaymentMethod	MonthlyCharges	TotalCharges	Churn
0	7590-VHVEG	Female	0	Yes	No	-1.280248	No	No phone service	DSL	No	...	No	No	No	No	Month-to-month	Yes	Electronic check	-1.161694	-0.994194	No
1	5575-GNVDE	Male	0	No	No	0.064303	Yes	No	DSL	Yes	...	Yes	No	No	No	One year	No	Mailed check	-0.260878	-0.173740	No
2	3668-QPYBK	Male	0	No	No	-1.239504	Yes	No	DSL	Yes	...	No	No	No	No	Month-to-month	Yes	Mailed check	-0.363923	-0.959649	Yes
3	7795-CFOCW	Male	0	No	No	0.512486	No	No phone service	DSL	Yes	...	Yes	Yes	No	No	One year	No	Bank transfer (automatic)	-0.747850	-0.195248	No
4	9237-HQITU	Female	0	No	No	-1.239504	Yes	No	Fiber optic	No	...	No	No	No	No	Month-to-month	Yes	Electronic check	0.196178	-0.940457	Yes

5 rows × 21 columns

2.6 编码/哑变量

本文使用的数据集中，离散型变量都不是有序变量，因此使用one_hot编码把这些特征转成哑变量。

# 分类变量转换为数值变量，one_hot编码
df_oh0 = df_nor.iloc[:, 1:]
print("one_hot编码前特征数量：{0}".format(df_oh0.shape))
df_oh1 = pd.get_dummies(df_oh0)
print("one_hot编码后特征数量：{0}".format(df_oh1.shape))

one_hot编码前特征数量：(7032, 20)
one_hot编码后特征数量：(7032, 47)

range_ = df_oh1.columns.tolist()
range_.remove("Churn_No")
df_oh = df_oh1.loc[:, range_]
df_oh.head()

	SeniorCitizen	tenure	MonthlyCharges	TotalCharges	gender_Female	gender_Male	Partner_No	Partner_Yes	Dependents_No	Dependents_Yes	...	Contract_Month-to-month	Contract_One year	Contract_Two year	PaperlessBilling_No	PaperlessBilling_Yes	PaymentMethod_Bank transfer (automatic)	PaymentMethod_Credit card (automatic)	PaymentMethod_Electronic check	PaymentMethod_Mailed check	Churn_Yes
0	0	-1.280248	-1.161694	-0.994194	1	0	0	1	1	0	...	1	0	0	0	1	0	0	1	0	0
1	0	0.064303	-0.260878	-0.173740	0	1	1	0	1	0	...	0	1	0	1	0	0	0	0	1	0
2	0	-1.239504	-0.363923	-0.959649	0	1	1	0	1	0	...	1	0	0	0	1	0	0	0	1	1
3	0	0.512486	-0.747850	-0.195248	0	1	1	0	1	0	...	0	1	0	1	0	1	0	0	0	0
4	0	-1.239504	0.196178	-0.940457	1	0	1	0	1	0	...	1	0	0	0	1	0	0	1	0	1

使用one_hot编码之后，特征从20个猛增到47个，除了3个连续型变量外，其余44个特征的值都是0或1，这样的数据可以认定是稀疏数据了。 机器学习能做分类的有很多模型，但是在稀疏数据上表现良好的模型主要是线性模型逻辑回归、线性支持向量机以及贝叶斯分类器。在一般数据集上树模型表现很好，比如决策树、随机森林、XGBOOST，还有KNN和神经网络的准确率也很高。 本文在用户流失预测模块会构建多种分类器，接着对比他们的准确率和运行时间，从而选择最适合的模型，然后对模型进行调参，提升模型性能。

2.7 特征选择

特征选择有多种方法，比如过滤法、基于模型的特征选择、PCA降维等，因为我们的数据特征除了标签列只有45个特征，算不上是高维数据，所以特征选择在这里就不做了。

Y = df_oh.iloc[:, -1]

1、无特征选择

X = df_oh.iloc[:, :-1]
X.shape

(7032, 45)

三、特征和流失的关联性——可视化

3.1 流失用户占比

df["Churn"].value_counts().plot.pie(labels=df['Churn'].unique()
                                    ,autopct='%.2f%%'
                                    ,fontsize=20
                                    ,figsize=(6, 6))

流失用户占比26.58%，样本存在不均衡的问题，记得这个问题，后面要先解决这个问题然后再建模。

3.2 用户属性分析

# 绘制条形图，一行绘制2个图，绘制多行
def plot_bar(list_name):
    """
    list_name: 需要绘制条形图的列表
    """
    ncols = 2 # 列数，固定一行画2个图
    nrows = math.ceil(len(list_name)/ncols) # 行数
    list_name2 = [list_name[i * ncols: i * ncols + ncols] for i in range(0, nrows)]
    fig, axes = plt.subplots(nrows, ncols, figsize=(20, 8 * nrows))
    for i in range(nrows):
        for j in range(ncols):
            if nrows == 1:
                ax = axes[j]
            else:
                ax = axes[i,j]
            # [i][j]超过列表下标会报错:list index out of...,使用try except避免出现这个BUG
            try:
                # plot参数：alpha颜色的透明度, rot轴标签旋转角度
                df0 = pd.crosstab(df[list_name2[i][j]], df["Churn"])
                df0.plot(kind='bar', ax=ax, alpha=0.5, fontsize=12, rot=0)
                # 图上加table，有点丑凑合看，主要是配合条形图来看
                table(ax
                      ,np.round(pd.DataFrame(df0['Yes']/(df0["No"] + df0["Yes"])*100).T, 2)
                      ,loc='upper center'
                      ,colWidths=[0.2] * df0.shape[0]
                     )
            except:
                pass

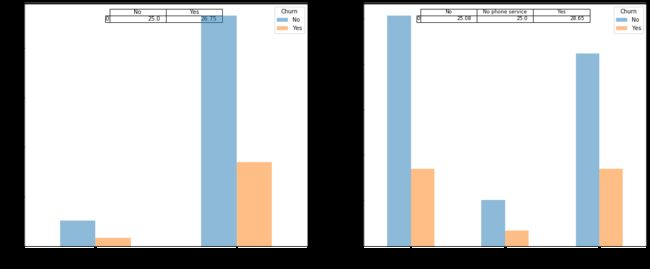
customer_list = ["gender","SeniorCitizen","Partner","Dependents"]
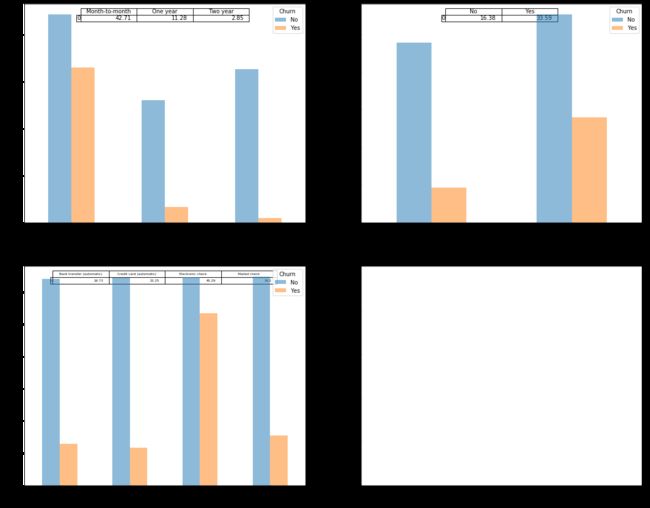
plot_bar(customer_list)

小结：从以上4个条形图可以看出，1、性别与用户流失基本无关；2、老年用户量虽然没有年轻人多，但是老年人群体的流失占比高于年轻人群体；3、有伴侣的群体的流失占比低于无伴侣的群体流失占比；4、有家属的群体的流失占比低于无家属的群体的流失占比。关注老年人群体、无伴侣群体、无家属群体是降低流失的切入口。

3.3 服务属性分析

PhoneService_list = ['PhoneService', 'MultipleLines']
plot_bar(PhoneService_list)

小结：从以上2个条形图可以看出，是否使用电话服务和多线服务与用户流失基本无关。

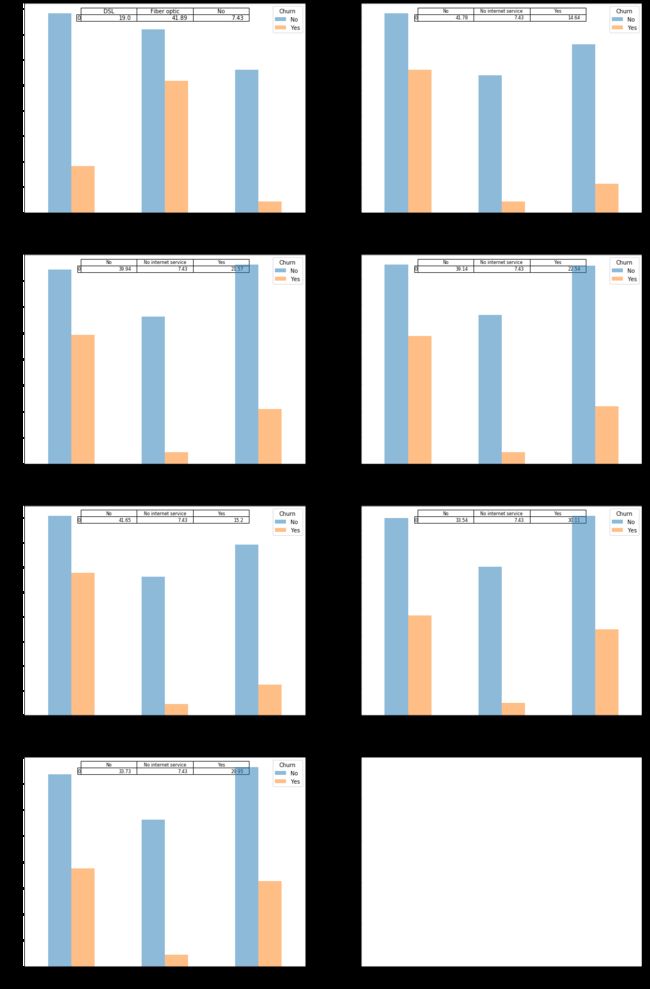
InternetService_list = ['InternetService', 'OnlineSecurity', 'OnlineBackup', 'DeviceProtection', 
                        'TechSupport', 'StreamingTV', 'StreamingMovies']
plot_bar(InternetService_list)

小结：从以上一组条形图可以看出，1、不使用互联网服务的用户流失占比最低；2、使用光纤的用户流失占比最高，高于数字用户线流失占比；3、不使用在线安全、在线备份、设备保护、技术支持服务的用户流失占比最高，高于使用了在线安全、在线备份、设备保护、技术支持服务的用户流失；4、是否使用流媒体电视、电影服务与用户流失基本无关。

3.4 消费属性分析

PaperlessBilling_list = ['Contract', 'PaperlessBilling', 'PaymentMethod']
plot_bar(PaperlessBilling_list)

小结：从以上3个条形图可以看出，1、合同期限越长用户流失占比越低，两年合同期流失占比低于一年合同期流失占比，一年合同期流失占比低于1个月合同期的流失占比；2、使用电子支票的流失占比最高，高于不使用电子支票的流失占比，电子支票和非电子支票的流失占比从高到低分别是：电子支票>邮寄支票>银行转账（自动）>信用卡（自动）。

以上可视化的特征基本都是离散变量，下面对特征中的连续变量进行可视化。

list1 = ['tenure', 'MonthlyCharges', 'TotalCharges']
ncols = 2 # 列数，固定一行画2个图
nrows = math.ceil(len(list1)/ncols) # 行数
list2 = [list1[i * ncols: i * ncols + ncols] for i in range(0, nrows)]
fig, axes = plt.subplots(nrows, ncols, figsize=(20, 8 * nrows))

for i in range(nrows):
    for j in range(ncols):
        try:
            # plot参数：alpha——颜色的透明度, rot——轴标签旋转角度。hist参数：bins——矩形条个数
            df[df["Churn"]=="Yes"][list2[i][j]].plot.hist(bins=30, ax=axes[i,j], title =list2[i][j], alpha=0.5, label='Yes')
            df[df["Churn"]=="No"][list2[i][j]].plot.hist(bins=30, ax=axes[i,j], title =list2[i][j], alpha=0.5, label='No')
        except:
            pass

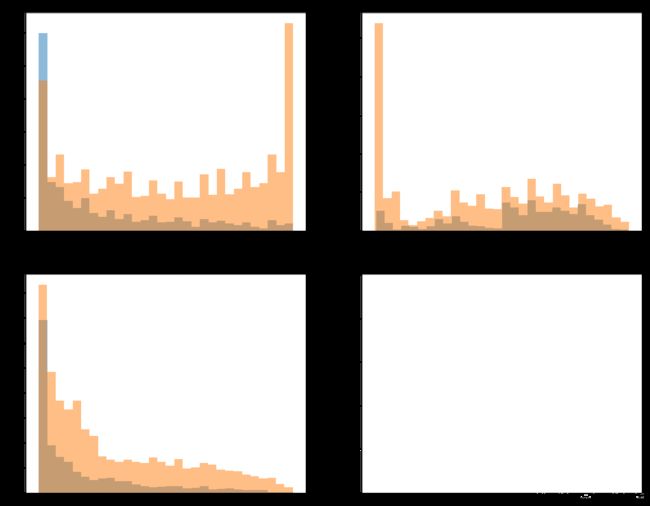
蓝色表示流失，橙色表示留存。

小结：从以上3个频率直方图可以看出，1、随着注册时间的增加，流失率表现出降低趋势，前6个月是用户流失的高频期，业务应该多关注注册6个月以内的用户；2、月消费在70-110之间的用户发生流失的可能性较高；3、随着用户的总消费的增多，流失率表现出明显的下降趋势，总消费在300左右的用户流失概率更大。
通过对特征和流失的关联性分析和可视化，可以给出容易流失的用户画像，具体如下：

四、用户流失预测

4.1 选择分类模型

这里构建了两个线性模型（逻辑回归、线性支持向量机）和多个非线性模型，使用交叉验证评估模型准确率并统计运行时间，希望能得到准确率高的、运行速度快的、可解释性强的模型。
我们的数据是稀疏数据，这一点在数据预处理——哑变量中已经讨论过，在模型开始训练前我们猜测以上模型的准确率最高的可能是在线性模型和神经网络中产生。

estimator = ["LR", "LinearSVC", "KNN", "DT", "RF", "XGB", "MLP"]
estimator_dict = {"LR":LR(random_state=0, n_jobs=-1) # 线性模型
                  ,"LinearSVC":LinearSVC() # 线性模型
                  ,"KNN":KNeighborsClassifier() # K近邻
                  ,"DT":DecisionTreeClassifier(random_state=0) # 树模型
                 ,"RF":RandomForestClassifier(random_state=0, n_jobs=-1) # 树模型，集成模型
                 ,"XGB":XGBC(random_state=0, n_jobs=-1) # 树模型，集成模型
                  ,"MLP":MLPClassifier(random_state=0) # 神经网络
                 }

score = {}
time_ = {}
# type = ["original", "pca", "chi2"]
# data_type = {"original":X, "pca":X_pca, "chi2":X_chi2}
type = ["original"]
data_type = {"original":X}
for m in range(len(estimator)):
    score2 = {}
    time_2 = {}
    for i in range(len(type)):
        start_time = time.time()
        score2[type[i]] = cross_val_score(estimator_dict[estimator[m]], data_type[type[i]], Y, cv=5).mean()
        time_2[type[i]] = time.time() - start_time
    score[estimator[m]] = score2
    time_[estimator[m]] = time_2

df_score = pd.DataFrame(score)
df_score

	LR	LinearSVC	KNN	DT	RF	XGB	MLP
original	0.803469	0.801904	0.772752	0.722694	0.787257	0.787968	0.783134

df_time = pd.DataFrame(time_)
df_time

	LR	LinearSVC	KNN	DT	RF	XGB	MLP
original	3.702679	1.619408	1.576289	0.170626	2.77854	4.232372	33.926442

从模型的准确率、运行时间、模型可解释性综合考虑，最终选择逻辑回归模型用来预测用户流失，因为逻辑回归的准确率最高、运行时间可以接受、模型可解释性强。

4.2 解决样本不均衡问题

4.2.1 为什么要解决样本不均衡？

从可视化章节得出该样本存在不均衡问题，如果不解决样本不均衡问题，模型会是什么样呢？
因为交叉验证没办法得到混淆矩阵，所以把数据集分成训练集和测试集。

X = data.iloc[:, :-2] # Churn_No列不需要
Y = data.iloc[:,-1]

Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, Y, test_size=0.3, random_state=0)

clf = LR() # 先用默认参数实例化
clf.fit(Xtrain, Ytrain)
clf.score(Xtest, Ytest)

0.8

在没解决样本不均衡问题的情况下，逻辑回归模型得到的分类准确率达到0.8，光看这个分数还是可以的，那这个模型召回率怎么样呢？接下来用混淆矩阵看看。

Ypredict = clf.predict(Xtest)

labels = [0, 1]

sns.set()
cm = confusion_matrix(Ytest, Ypredict, labels=labels)
cm_normalized = cm/cm.sum(axis=1)[:, np.newaxis]
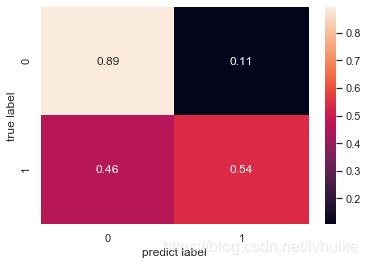
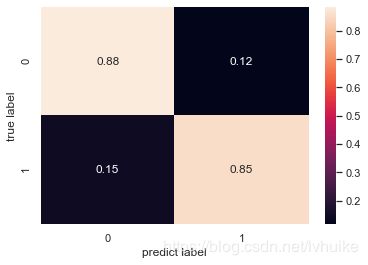
sns.heatmap(cm_normalized,annot=True)
plt.xlabel('predict label')
plt.ylabel('true label')

观察混淆矩阵发现，实际流失预测流失的TP仅为0.54，跟随机（瞎猜）差不多，但是实际留存预测留存的FP达到了0.89，模型更倾向于把结果预测为留存，模型把所有测试样本都预测为留存准确度也能达到0.89。这就是样本不均衡带来的影响，以及为什么要解决样本不均衡的原因。接下来对样本不均衡的问题做点什么吧。

4.2.2 解决样本不均衡问题

样本不均衡的问题怎么解决呢？主流的是采样法，通过重复样本的方式来平衡标签，有上采样（增加少数类的样本），还有下采样（减少多数类的样本），这里采用上采样的方法。

print("上采样前样本大小:{0}".format(X.shape[0]))
sm = SMOTE(random_state=42)
Xdata, Ydata = sm.fit_sample(X, Y)
bal_data = pd.concat([Xdata, Ydata], axis=1)
print("上采样后样本大小:{0}".format(bal_data.shape[0]))

上采样前样本大小:7032
上采样后样本大小:10326

bal_data['Churn_Yes'].value_counts()

1    5163
0    5163
Name: Churn_Yes, dtype: int64

4.3 逻辑回归调参

X = bal_data.iloc[:, :-1]
Y = bal_data.iloc[:,-1]

4.3.1 train_test_split参数random_state

score_list = []

range_ = range(0,500,10)

for i in range_:
    # 随机数的选择也会影响结果，大概测试几个发现0的结果最好
    Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, Y, test_size=0.3, random_state=i)
    clf = LR()
    clf.fit(Xtrain, Ytrain)
    score = clf.score(Xtest, Ytest)
    score_list.append(score)

plt.figure(figsize=(15, 6))
plt.plot(range_, score_list)
plt.show()
print("最高准确度是：{:.3f}".format(max(score_list)),
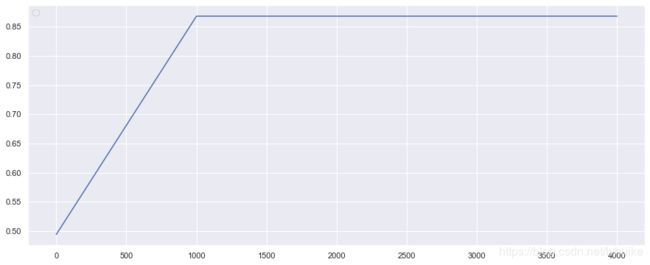
      "\t最好random_state是：{0}".format(list(range_)[score_list.index(max(score_list))]))

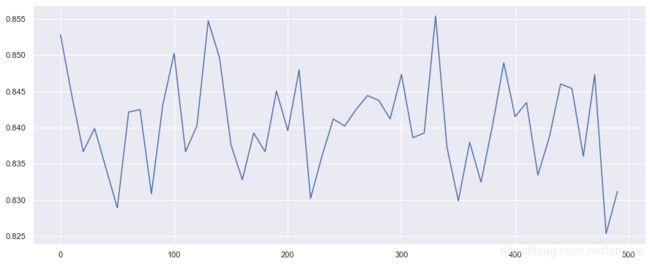
最高准确度是：0.855 	最好random_state是：330

从折线图和数据结果可以看到，当使用LR默认参数时，train_test_split的参数random_state在330时，模型准确度达到0.855。这里，train_test_split的参数random_state就选取为330。

Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, Y, test_size=0.3, random_state=330)

4.3.2 逻辑回归调参

1、solver

score_list = []
cvs_score_list = []

solver_list = ["liblinear", "lbfgs", "newton-cg", "sag", "saga"]
for i in solver_list:
    clf = LR(solver=i)
    # train_test_split得分
    clf = clf.fit(Xtrain, Ytrain)
    score = clf.score(Xtest, Ytest)
    score_list.append(score)
    # 交叉验证得分
    cvs_score_list.append(cross_val_score(clf, X, Y, cv=5).mean())

graph = [score_list, cvs_score_list]
color = ["green", "black"]
label = ["train_test_split", "cross_val_score"]

plt.figure(figsize=(15,6))
for i in range(len(graph)):
    plt.plot(solver_list, graph[i], color[i], label=label[i])
plt.legend(loc=1)
plt.show()

print("1、最高准确度是：{:.3f}".format(max(score_list)),
      "\tsolver是：{0}".format(solver_list[score_list.index(max(score_list))]))
print("2、交叉验证最高准确度是：{:.3f}".format(max(cvs_score_list)),
      "\tsolver是：{0}".format(solver_list[cvs_score_list.index(max(cvs_score_list))]))

1、最高准确度是：0.868 	solver是：newton-cg
2、交叉验证最高准确度是：0.834 	solver是：newton-cg

从以上结果看出，1、把数据集分成训练集测试集的效果比交叉验证的效果更好些，后面模型评估就不用交叉验证了；2、newton-cg的效果最好；3、调整solver参数使得模型效果从0.855提升到了0.868。

2、max_iter

score_list = []

max_iter_list = range(0, 5000, 1000)

for i in max_iter_list:
    clf = LR(solver='newton-cg', max_iter=i)
    
    clf = clf.fit(Xtrain, Ytrain)
    score = clf.score(Xtest, Ytest)
    score_list.append(score)

plt.figure(figsize=(15,6))
plt.plot(max_iter_list, score_list)
plt.legend(loc=2)
plt.show()

print("1、最高准确度是：{:.3f}".format(max(score_list)),
      "\tmax_iter是：{0}".format(list(max_iter_list)[score_list.index(max(score_list))]))

1、最高准确度是：0.868 	max_iter是：1000

从以上结果可以看出，1、max_iter从1000开始，最高准确度就达到了0.868；2、调max_iter前准确度0.868，调参后最高准确度依然是0.868，没什么变化。

3、penalty和C和过拟合

# 这里看看有没有过拟合
l1 = []
l2 = []
l1test = []
l2test = []

c_list = np.linspace(0.05, 1, 19)
for i in c_list:
#     lr1 = LR(penalty='l1', solver='newton-cg', C=i, max_iter=1000)
    lr2 = LR(penalty='l2', solver='newton-cg', C=i, max_iter=1000)  # newton-cg支支持l2
    
#     lr1.fit(Xtrain, Ytrain)
#     l1.append(accuracy_score(lr1.predict(Xtrain), Ytrain))
#     l1test.append(accuracy_score(lr1.predict(Xtest), Ytest))
    
#     cvs_l1.append(cross_val_score(lr1, X, Y,cv=5).mean())
    
    lr2.fit(Xtrain, Ytrain)
    l2.append(accuracy_score(lr2.predict(Xtrain), Ytrain))
    l2test.append(accuracy_score(lr2.predict(Xtest), Ytest))
    
#     cvs_l2.append(cross_val_score(lr2, X, Y,cv=5).mean())

l1 = [np.nan]*19

l1test = [np.nan]*19

graph = [l1, l2, l1test, l2test]
color = ["green", "black", "lightgreen", "gray"]
label = ["l1", "l2", "l1test", "l2test"]

plt.figure(figsize=(15,6))
for i in range(len(graph)):
    plt.plot(c_list, graph[i], color[i], label=label[i])

plt.legend(loc=0)
plt.show()

print("1、训练集最高准确度是：{:.3f}".format(max(l2)),
      "\tC是：{0}".format(c_list[l2.index(max(l2))]))
print("2、验证集最高准确度是：{:.3f}".format(max(l2test)),
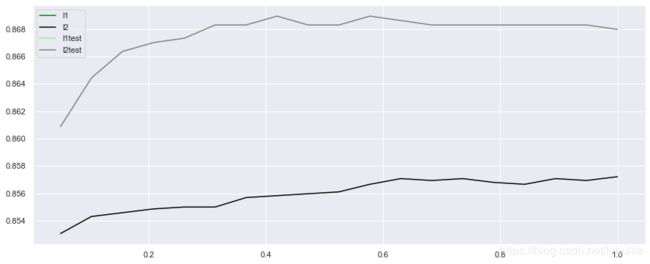
      "\tC是：{0}".format(c_list[l2test.index(max(l2test))]))

1、训练集最高准确度是：0.857 	C是：1.0
2、验证集最高准确度是：0.869 	C是：0.41944444444444445

从以上结果可以看出，1、验证集和训练集上的分数都比较高，这说明不存在欠拟合，验证集上的分数没有低于训练集，这说明不存在过拟合，模型的性能还是比较稳定的；2、参数C调整前，分数是0.868，调整C之后模型的最高得分是0.869，说明调整C对模型准确度的提升起到了正面积极的作用。

4、multi_class 和 random_state

multi_mul = []
mul_ovr = []

random_list = range(0,200,50)


for i in random_list:
    clf1 = LR(penalty='l2', solver='newton-cg', max_iter=1000, C=0.41944444444444445, random_state=i, multi_class="multinomial")
    clf2 = LR(penalty='l2', solver='newton-cg', max_iter=1000, C=0.41944444444444445, random_state=i, multi_class="ovr")

    clf1.fit(Xtrain, Ytrain)
    multi_mul.append(clf1.score(Xtest, Ytest))
    
    clf2.fit(Xtrain, Ytrain)
    mul_ovr.append(clf2.score(Xtest, Ytest))   

graph = [multi_mul, mul_ovr]
color = ["green", "gray"]
label = ["multinomial", "ovr"]

plt.figure(figsize=(15,6))
for i in range(len(graph)):
    plt.plot(random_list, graph[i], color[i], label=label[i])

plt.legend(loc=0)
plt.show()

print("1、multinomial最高准确度是：{:.3f}".format(max(multi_mul)))
print("2、ovr最高准确度是：{:.3f}".format(max(mul_ovr)))

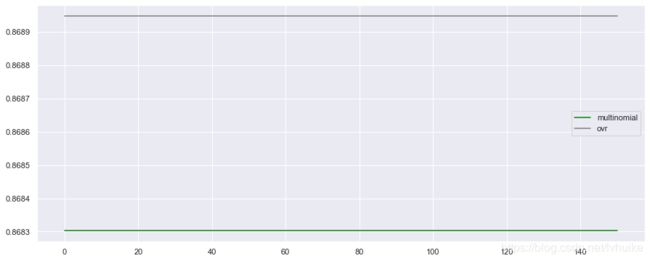
1、multinomial最高准确度是：0.868
2、ovr最高准确度是：0.869

从以上结果可以看出，1、random_status取哪个值效果都一样，因此random_status用0；2、ovr的效果比multinomial效果好，调参之前分数是0.869，调参之后最好分数是0.869，因此参数multi_class用ovr。

clf = LR(solver='newton-cg', penalty='l2', max_iter=1000, C=0.41944444444444445, random_state=0)
clf = clf.fit(Xtrain, Ytrain)
clf.score(Xtest, Ytest)

0.8689477081988379

通过学习曲线调整LR的参数，使得模型准确率从0.8提升到0.8689477081988379，提升的幅度还是挺大的，这就是调参的力量。

4.3.3 带交叉验证的网格搜索

交叉验证虽然不用每个参数画学习曲线，但是搜索速度比较慢，一般可以先用学习曲线找到范围，再用交叉验证搜索最佳取值。

param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100]
             , 'max_iter': [500, 1000, 2000, 3000]}
clf0 = LR()
grid_search = GridSearchCV(clf0, param_grid=param_grid, cv=5)
grid_search.fit(Xtrain, Ytrain)
print("测试集上的最好分数：{:.3f}".format(grid_search.score(Xtest, Ytest)))

测试集上的最好分数：0.861

利用交叉验证得到一个在训练集上准确度为0.861的模型。接下来看看在训练集上的分数和最好的参数。

print("最好的参数：{0}".format(grid_search.best_params_))
# grid_search.best_score_保存的是交叉验证的平均精度，是在训练集上进行交叉验证得到的
# grid_search.score得到的是在整个训练集上训练的模型
print("交叉验证的得分：{:.3f}".format(grid_search.best_score_))

最好的参数：{'C': 100, 'max_iter': 1000}
交叉验证的得分：0.850

print("模型参数：{0}".format(grid_search.best_estimator_))

模型参数：LogisticRegression(C=100, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=1000,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)

从以上结果可以看出，使用网格搜索得到的分数是0.861，使用网格搜索得到的交叉验证得分是0.850，普通调参得到的分数是0.869，最终还是选择普通调参得到的模型。其实这里网格搜索只有2个参数，可以选择更多的参数，但是更多参数就意味着搜索速度指数增加。

4.4 模型评估

只用准确率评估模型不够全面，因为如果样本不均衡的话，模型很容易倾向于预测多数类，因此使用混淆矩阵和ROC曲线评估模型的性能。

1、混淆矩阵

# 混淆矩阵
# TN FP
# FN TP
Ypredict = clf.predict(Xtest)

labels = [0, 1]

sns.set()
cm = confusion_matrix(Ytest, Ypredict, labels=labels)

print("混淆矩阵：\n{0}".format(cm))
# 精度（TP+TN）/(TP+TN+FP+FN)
# print("\n精度是：{:.3f}".format((cm[0,0]+cm[1,1])/cm.sum()))
# 准确率TP/(TP+FP)
# print("\n准确率是：{:.3f}".format(cm[1,1]/(cm[0,0]+cm[1,1])))
# 召回率TP/(TP+FN)
# print("\n召回率是：{:.3f}".format(cm[1,1]/(cm[1,0]+cm[1,1])))

# 准确率、召回率、f1分数
# f1分数 2*（准确率 * 召回率）/（准确率 + 召回率）
print("\n分类报告：\n{0}".format(classification_report(Ytest, Ypredict, target_names=["0", "1"])))

cm_normalized = cm/cm.sum(axis=1)[:, np.newaxis]
sns.heatmap(cm_normalized,annot=True)
plt.xlabel('predict label')
plt.ylabel('true label')

混淆矩阵：
[[1353  178]
 [ 228 1339]]

分类报告：
              precision    recall  f1-score   support

           0       0.86      0.88      0.87      1531
           1       0.88      0.85      0.87      1567

    accuracy                           0.87      3098
   macro avg       0.87      0.87      0.87      3098
weighted avg       0.87      0.87      0.87      3098

从混淆矩阵和分类报告可以看出，模型的性能还是不错的，准确率、召回率和f1分数都比较高而且均衡。

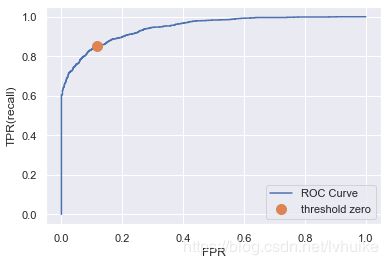
2、ROC曲线

fpr, tpr, thresholds = roc_curve(Ytest, clf.decision_function(Xtest))

plt.plot(fpr, tpr, label="ROC Curve")
plt.xlabel("FPR")
plt.ylabel("TPR(recall)")
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10, label='threshold zero')
plt.legend(loc=4)

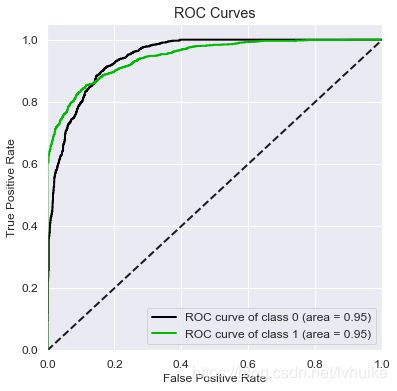
vali_proba_df = pd.DataFrame(clf.predict_proba(Xtest))
skplt.metrics.plot_roc(Ytest, vali_proba_df,
                      plot_micro=False, figsize=(6,6),
                      plot_macro=False)

ROC曲线 AUC值：area under a curve,指在曲线下面的面积，该面积取值范围通常在0.5-1，0.5代表随即判断，1则代表完美的模型。 通常AUC达到0.75以上就可以接受，达到0.85以上就是非常不错的模型了。

ROC曲线捕捉模型少数类的判断，纵坐标代表判对一个，横坐标代表判错一个，对角线表示模型要判对一个的同时要判错一个，AUC越大代表模型越好。 这个图说明模型预测标签为1的样本的效果是非常好的。

从以上2个ROC曲线可以看出，召回率高于0.8时，假正率低于0.2，模型还是不错的。

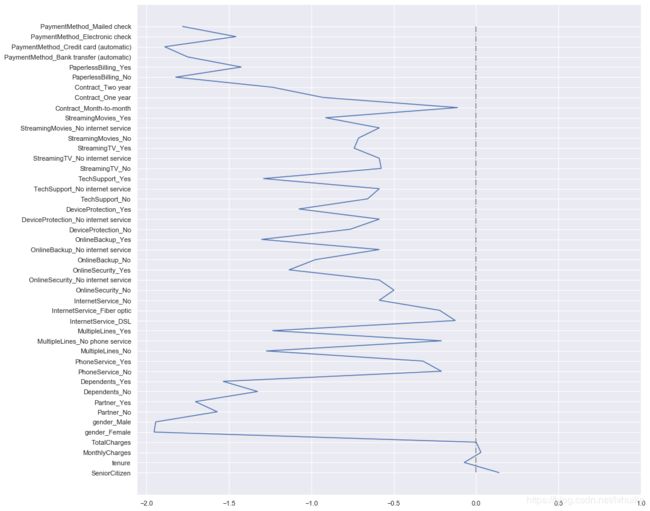
4.5 特征重要程度

x_label = Xtrain.columns.to_list()
y_label = clf.coef_.tolist()[0]
zero_label = [0]*len(x_label)
plt.figure(figsize=(15,15))
plt.plot(y_label, x_label)
plt.plot(zero_label, x_label, color='gray', linestyle='-.')
plt.xticks(np.arange(-2, 1.05, 0.5))
plt.show()

从图中可以看出，1、有很多特征都被模型学习了，因为特征工程里没有特征选择操作；2、大多数特征对流失都是负相关，即特征值增加，流失概率就会降低。

五、总结和建议

5.1 流失用户画像

通过可视化和数据，可以总结出流失概率高的用户画像：1、用户属性：老年用户、无伴侣用户、无家属用户更容易流失；2、互联网服务属性：使用光纤、无在线安全、在线备份、设备保护、技术支持服务的用户更容易流失；3、消费属性：1个月合同期限、电子支票支付、注册时间3个月内、月消费额在70-110之间、总消费额低于300的用户更容易流失。

5.2 建议

针对以上结论，提出如下建议： 1、用户方面：针对老年用户、无伴侣用户、无家属用户推出亲情套餐等优惠活动，一方面可以增加新用户，另一方面通过加强与其他用户的关联降低流失； 2、互联网方面：针对使用光纤的用户，重点在于提升用户的网络体验，需要技术部门提高网络指标； 针对无在线安全、在线备份、设备保护、技术支持服务的用户，应重点推广介绍这些增值服务，通过推出优惠活动让用户体验并购买，如首月免费体验。 3、消费方面：针对单月合同的用户，建议通过年合同折扣活动将其转化成年合同用户，从而降低流失。 针对使用电子支票的用户，建议向其推出信用卡或银行转账的满减或优惠券，引导用户改变支付方式。 针对新注册用户，推出半年或一年优惠券或活动，降低用户流失高频期内的流失的可能性。