超级详细 倍增法 实现 LCA
描述:倍增法用于很多算法当中,通过字面意思来理解就是翻倍增加嘛,这里着重讲使用倍增法在树中的应用求LCA;
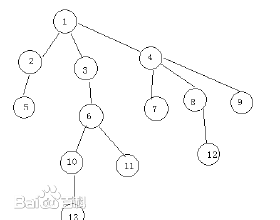
LCA是啥呢 在一棵树当中 lca表示的是两个节点最近公共祖先, 大家看这课树哈节点5 ,3的lca就是1,13和11的LCA就是6。节点8,12的lca就是8,那么我们如何通过被增来实现LCA呢。
首先请大家认真看下面的分析。
depth[x],表示x节点的深度。
大家看下这个数组 grand[x][i] ,这个数组表示标号为x节点向上跳2^i步的节点。例如grand[5][0]=2,因为5这个节点向上跳2^0次方个就是2,当然所有节点向上跳一个就是他的父亲节点,
得到grand[x][0]=他的爸爸,
那grand[x][1]=什么呢?等于grand[grand[x][0]][0];
既grand[x][i]=grand[grand[x][i-1]][i-1],为什么呢,2^4=2^3+2^3,表示 x向上跳2的i次的节点=x向上跳i-1次方的这个节点向上跳i-1次方,有点绕口。例如 grand[13][2]=grand[6][2]=g[g[rand][i-1]][i-1];
有了这个预处理那我们是不是可以得到每一个节点向上跳i格呢,然后就是i的取值范围为1<=i<=log2(n),向下取整n表示节点个数,也就是说grand[x][log2(n)]就至少可以跳到根节点甚至上面,当然上面啥都没有。
我们这里还有一个数组 gw[x][i],表示x节点向上跳2^i次方的距离(权)。同样的有gw[x][i]=gw[x][i-1]+gw[grand[x][i-1]][i-1],这个公式表示x到他向上跳2的i次方那个节点的距离=x跳2^i-1次方的距离加上,他向上跳2^i-1次方这个点到他上面跳2^i-1次方的距离。
例如1,3,6,10,13,他们之间的边的权等于 2 4 3 6,既gw[13][0]=他爸爸10到他的距离等于6,gw[]13[2]=gw[13][1]+gw[6][1];。
其实我们可以自己加很多类似的数组
例如max[x][i]啊表示 x向上跳2^i次方的边的最大的那条边。这里就不一一举例子子了
现在有了这些预处理。我下面是用dfs实现的预处理;
就看如何实现LCA了吧,
首先 给定两个节点。假如给定的是a=13,b=12.。要我们求他们的lca ,首先第一步 我们要把他们调整到同一深度,既把a向上跳一个步这样他们的深度就相同的了。我们是把深度高的向上调。调整跟深度低的一样。
然后就两个节点一起向上跳一个2^j,首先我们j从log2(n)=3开始跳,跳到0。我们要跳到他们lca的下面两个节点。既3和4,既可以跳的节点是他们不相同并且不超出根节点(grand[a][j]!=grand[b][j]),这里是j=1的时候跳了,j=1因为(grand[a][j]!=grand[b][j]);就执行(a=grand[a][j],b=grand[b][j])a就跳到了3,b就跳到了4,其余的j就不可以跳因为j=3,2就到根的上面了j=0他们就想等了。跳到那,最后退出,grand[a][0]就是他们的lca了。
这就是程序的执行过程。下面看代码
模板体 :hdu2586
代码:
#include
#include
#include
#include
#include
#define max 40001
#define maxl 25
using namespace std;
typedef struct
{
int from,to,w;
}edge;//这个结构体用来存储边
vectoredges;
vector G[max];
//保存边的数组
int grand[max][maxl],gw[max][maxl];//x向上跳2^i次方的节点,x到他上面祖先2^i次方的距离
int depth[max];//深度
int n,m,N;
void addedge(int x,int y,int w)//把边保存起来的函数
{
edge a={x,y,w},b={y,x,w};
edges.push_back(a);
edges.push_back(b);
G[x].push_back(edges.size()-2);
G[y].push_back(edges.size()-1);
}
void dfs(int x)//dfs建图
{
for(int i=1;i<=N;i++)//第一个几点就全部都是0咯,第二个节点就有变化了,不理解的话建议复制代码输出下这些数组
{
grand[x][i]=grand[grand[x][i-1]][i-1];
gw[x][i]=gw[x][i-1]+gw[grand[x][i-1]][i-1];
// if(grand[x][i]==0) break;
}
for(int i=0;i depth[b]) swap(a, b);//保证a在b上面,便于计算
int ans = 0;
for(int i = N; i >= 0; i--) //类似于二进制拆分,从大到小尝试
if(depth[a] < depth[b] && depth[grand[b][i]] >= depth[a])//a在b下面且b向上跳后不会到a上面
ans +=gw[b][i], b=grand[b][i];//先把深度较大的b往上跳
for(int j=N;j>=0;j--)//在同一高度了,他们一起向上跳,跳他们不相同节点,当全都跳完之后grand【a】【0】就是lca,上面有解释哈。
{
if(grand[a][j]!=grand[b][j])
{ ans+=gw[a][j];
ans+=gw[b][j];
a=grand[a][j];
b=grand[b][j];
}
}
if(a!=b)//a等于b的情况就是上面土色字体的那种情况
{
ans+=gw[a][0],ans+=gw[b][0];
}
return ans;
}
int main()
{ int t ;
scanf("%d",&t);
while(t--)
{ scanf("%d%d",&n,&m);
for(int i=1;i