常用图像卷积核小结

0. 前言

图像的卷积或滤波操作在各种场合应用很普遍，如各种滤镜、卷积神经网络等。下面这张图片就很能说明图像卷积的基本原理了：

CSDN上这篇博客对图像卷积的解释也很到位。在此先总结几个点：

• 卷积操作的主要目的就是对图像进行降维以及特征提取；
• 卷积核往往是行数和列数均为奇数的矩阵，这样中心较好定位；
• 卷积核元素的总和体现出输出的亮度，若元素总和为1，卷积后的图像与原图像亮度基本一致；若元素总和为0，则卷积后的图像基本上是黑色，其中较亮的部分往往就是提取出图像的某种特征；
• 滤波实际上就是Same模式的卷积操作，也就是说滤波后图像的大小不变，各种滤镜和照片的风格化就是使用不同的滤波器对图像进行操作。因此卷积核、滤波器本质上都是一个东西；
• 高通滤波器（High Pass Filter, HPF）表示仅允许图像中高频部分（即图片中变化较剧烈的部分）通过，往往用于对图像进行锐化处理、增强图像中物体边缘等。如Sobel算子、Prewitt算子、锐化滤波器等；
• 低通滤波器（Low Pass Filter, LPF）表示仅允许图像中低频部分（即图片中变化较平缓的部分）通过，往往用于对图像进行模糊/平滑处理、消除噪点等。如高斯滤波器、均值滤波器等；

本文在此将常用的卷积核及其对应的意义总结记录一下，以便随时复习。

1. 均值滤波和高斯滤波

1.1 简介

这两个滤波器有如下两个共同点：

• 滤波器中元素之和为1，输出亮度与输入基本一致；
• 均为低通滤波器，主要用于图像模糊/平滑处理、消除噪点；
• 核越大，模糊程度越大；

其中均值滤波器从名字就可以看出，每个元素值都一样，是卷积核元素个数的倒数，这样每个输出像素就是其周围像素的均值。一个$3\times 3$的均值滤波器如下所示：
$$\left[\begin{array}{ccc}1/9& 1/9& 1/9\\ 1/9& 1/9& 1/9\\ 1/9& 1/9& 1/9\end{array}\right]$$

高斯滤波器虽然元素总和也为1，但每个位置的权重不一样，权重在行和列上的分布均服从高斯分布，故称高斯滤波器。高斯分布的标准差越大，则模糊程度越大。一个$3\times 3$标准差为1的高斯滤波器如下所示：
$$\left[\begin{array}{ccc}1/16& 2/16& 1/16\\ 2/16& 4/16& 2/16\\ 1/16& 2/16& 1/16\end{array}\right]$$

1.2 示例

这两个滤波器主要作用均为模糊图像，或在图像预处理中消除图像中的噪点：

2. 锐化卷积核

2.1 简介

锐化卷积核从名字就可以看出，主要作用就是对图片进行锐化操作，也就是让图像的边缘更加锐利。图像的边缘往往就是变化较大的地方，也就是图像的高频部分，因此锐化卷积核就是一种高通滤波器。一个$3\times 3$的锐化卷积核如下所示：
$$\left[\begin{array}{ccc}-1& -1& -1\\ -1& 9& -1\\ -1& -1& -1\end{array}\right]$$

可见该卷积核就是计算中心位置像素与周围像素的差值，差值越大则表示该元素附近的变化越大（频率越大），输出值也就越大，因此是高频滤波器的一种。锐化卷积核元素总和如果是0，则有提取图像边缘信息的效果。

2.2 示例

锐化卷积核作用为突出图像中物体的边缘，相当于给物体描边：

3. 一阶微分算子

3.1 简介

图像中物体的边缘往往就是变化较为剧烈的部分（高频部分），对于一个函数来说，变化越剧烈的地方，对应的导数的绝对值也就越大。图像就是一种二元函数，$f(x,y)$表示$(x,y)$处像素的值，因此导数除了大小，还有方向。那么求图像在某方向上的一阶导数（或称图像的梯度），也就可以反映出图像在该处的变化程度，变化程度越快，在该方向的垂直方向可能就存在物体的边缘。

一阶微分算子可以计算出某个方向上物体的边缘，但往往对噪声较为敏感，且边缘检测敏感度依赖于物体的大小。

3.2 Prewitt算子

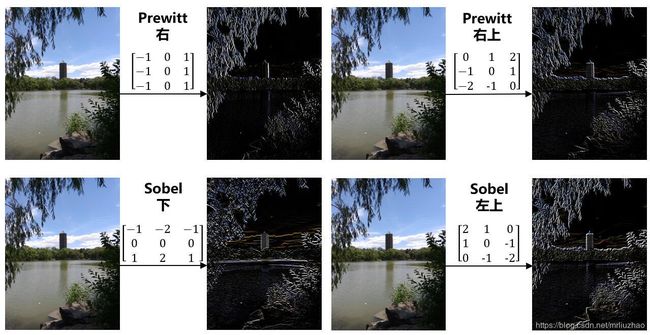
Prewitt算子就是对图像进行差分来近似对图像的某个部分求一阶导数。由于导数还具有方向性，因此同样大小的Prewitt算子还有8种不同的类型，目的在于求上、下、左、右、左上、左下、右上、右下8个方向上的梯度。其中求向右梯度的$3\times 3$Prewitt算子如下所示：
$$\left[\begin{array}{ccc}-1& 0& 1\\ -1& 0& 1\\ -1& 0& 1\end{array}\right]$$

类似地，求向右上方梯度的$3\times 3$Prewitt算子则为：
$$\left[\begin{array}{ccc}0& 1& 1\\ -1& 0& 1\\ -1& -1& 0\end{array}\right]$$

3.3 Sobel算子

Sobel算子则是Prewitt算子的改进版，对中间的元素适当进行了加权，Sobel算子之于Prewitt算子类似于高斯滤波之于均值滤波。同样Prewitt算子，Sobel算子一样考虑方向，计算向上梯度的$3\times 3$Sobel算子如下所示：
$$\left[\begin{array}{ccc}1& 2& 1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right]$$

类似地，求向左上方梯度的$3\times 3$Sobel算子则为：
$$\left[\begin{array}{ccc}2& 1& 0\\ 1& 0& -1\\ 0& -1& -2\end{array}\right]$$

3.4 示例

使用一阶梯度可以提取出图像中物体在某个具体方向上的边缘：

4. 二阶微分算子

4.1 简介

上一小节介绍的Prewitt算子和Sobel算子都是近似对图像进行一阶导数的计算，只能提取出某个具体方向的边缘。由微积分的知识可知，一个函数的二阶导数为0时，代表此处的一阶导数取得极值，对应地也就表明原函数在此处的变化最大。比如著名的Sigmoid函数及其一阶导数、二阶导数的图像如下：

因此往往还可以根据图像的二阶导数过零点的位置，来预测图像中变化最剧烈的地方，也许对应物体的边缘。与一阶微分算子不同，这些二阶微分算子对边缘的计算具有旋转不变性，也就是可以检测出各个方向上的边缘。

4.2 Laplace算子

Laplace算子可以近似计算出图像的二阶导数，具有旋转不变性，也就是可以检测出各个方向的边缘。

Laplace算子分为两种，分别考虑4-邻接（D4）和8-邻接（D8）两种邻域的二阶微分。一个$3\times 3$的4-邻接Laplace算子如下所示：
$$\left[\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$$

8-邻接的$3\times 3$Laplace算子则考虑到斜对角方向上的梯度：
$$\left[\begin{array}{ccc}1& 1& 1\\ 1& -8& 1\\ 1& 1& 1\end{array}\right]$$

可以看出D8 Laplace算子与锐化卷积核类似，锐化卷积核计算的是中心像素减去周围像素的差值（中心权重为正，周边权重为负）；而Laplace算子则是周围像素之和减去中心像素的差值（中心权重为负，周边权重为正）。

4.3 LoG算子

Laplace算子对噪声依然很敏感。因此常常先使用高斯滤波器对图像进行平滑操作，再使用Laplace算子计算二阶微分。二者结合称为LoG算子（Laplacian of Gaussian），该算子可以更加稳定地计算图像的二阶微分。常用的$5\times 5$的LoG算子如下所示：
$$\left[\begin{array}{ccccc}0& 0& 1& 0& 0\\ 0& 1& 2& 1& 0\\ 1& 2& -16& 2& 1\\ 0& 1& 2& 1& 0\\ 0& 0& 1& 0& 0\end{array}\right]$$

4.4 DoG算子

LoG算子的计算量较大，因此有数学家发明了DoG（Difference of Gaussians）算子来近似LoG算子。DoG算子翻译为高斯差分算子，从名称上可以看出，就是使用两个标准差不同的高斯滤波器对图像进行滤波操作，再将滤波后的两个结果相减，最后的结果可以近似LoG算子。其中涉及到的数学理论较为复杂，在此暂不讨论。

4.5 示例

二阶微分算子可以提取出图像中物体在各个方向上的边缘：