概率统计（四）方差分析

对方差分析的简单理解

方差分析主要研究分类变量作为自变量时，对因变量的影响是否是显著的。
以焦虑症治疗为例，现有两种治疗方案：认知行为疗法（CBT）和眼动脱敏再加工法（EMDR）。我们招募10为焦虑症患者作为志愿者，随机分配一半的人接受为期五周的CBT，另一半接受为期五周的EMDR。在治疗结束时，要求每位患者都填写状态特质焦虑问卷（STAI），也就是一份焦虑度测量的自我评测报告。

• 在这个实验设计中，治疗方案是两水平（CBT、EMDR）的组间因子，STAI是因变量，治疗方案是自变量。
• 由于在每种治疗方案下观测数相等，因此这种设计也称为均衡设计，若观测数不同，则称作非均衡设计。
• 因为仅有一个类别型变量，因此实验设计又被称为单因素方差分析，或进一步称为单因素组间方差分析，方差分析主要通过F检验来进行效果评测，若治疗方案的F检验显著，则说明五周后两种疗法的STAI得分均值不同。

假设对治疗方案差异和它随时间的改变都感兴趣，则将两个设计结合起来即可：随机分配五位患者到CBT，另外五位到EMDR，在五周和六个月后分别评价他们的STAI结果。

• 此时时间是两水平（五周、六月）的组内因子，因为每位患者在所有水平下都进行了测量，所以这种统计设计称单因素组内方差分析。
• 又由于每个受试者都不止一次被测量，也称作重复测量方差分析。

先假设对治疗方案差异和它随时间的改变都感兴趣则将两个设计结合起来即可：随机分配五位患者到CBT，另外五位到EMDR，在五周和六个月后分别评价它们的STAI结果。

• 疗法和时间都作为因子时，我们既可分析疗法的影响和时间的影响，又可分析疗法和时间的交互影响，前两个称作主效应，交互部分称作交互效应
• 当设计包含两个甚至更多的因子时，便是因素方差分析设计，比如两因子时称作双因素方差分析，三因子时称作三因素方差分析，以此类推。
• 若因子设计包括组内和组间因子，又称作混合模型方差分析，当前的例子就是典型的双因素组合模型方差分析。

现将上面的实验设计稍微做些扩展，众所周知，抑郁症对病症治疗有影响，而且抑郁症和焦虑症常常同时出现，即使受试者被随机分配到不同的治疗方案中，在研究开始时，两组疗法中的患者抑郁水平就可能不同，任何治疗后的差异都有可能是最初的抑郁水平不同导致的，而不是实验操作的问题。

• 抑郁症也可以解释因变量的组间差异，因此它常称为混淆因素，由于你对抑郁症不感兴趣，因此它也被称为干扰变数。
• 假设招募者使用能以一种的自我测评报告，比如白氏抑郁症量表（BDI）记录了他们的抑郁水平，那么你可以在评测疗法类型的影响前，对任何抑郁水平的组间差异进行统计性调整，本案例中BDI为协变量，该设计为协方差分析（ANCOVA）。
• 以上设计只记录了单个因变量情况（STAI），为增强研究的有效性，可以对焦虑症进行其他的测量，当因变量不止一个时，设计被称作多元方差分析（MANOVA），若协变量也存在，那么就叫多元协方差分析（MANCOVA）。

单因素方差分析

1.推导过程

假设我们现在有若干品种的小麦，要在某一地区播种，我们想知道这些品种的产量有没有显著区别，为此我们先设计了一个田间实验，取一大块地将其分成形状大小都相同的n小块，设供选择的,品种有k个，打算在其中的n₁小块种植品种1，n₂小块种植品种2等等，n₁ + n₂ +… + n_n = n。

接下来我们使用方差分析的方法去看不同小麦品种的产量是否有显著差异：

• 设问题中涉及一个因素A，有k个水平，以Y_ij记第i个水平的第j个观察值，如上例Y_ij是种植品种i的第j小块地上的亩产量，模型为$$Y_{ij}=a_i+e_{ij}，i=1,...,k，j=1,...,n_i$$
• a_i表示水平i的理论平均值，称为水平i的效应。在小麦例子中，a_i就是品种i的平均亩产量，e_ij就是随机误差，并且我们假定$$E(e_{ij})=0,0<Var(eij)={\delta }^2<\infty ，一切e_{ij}独立同分布$$
• 因素A的个水平高低优劣，取决于其理论平均a_i的大小。如果a_i全相同，表示因素A对所考察的指标Y其实无影响，这时我们说因素A的效应不显著，否则说它显著，因此我们的H₀假设为：$$H_0：a_1=a_2=a_3=...=a_k$$
• 为检验该假设，我们要分析为什么各个Y_ij会有差异？从模型看，一是各a_i可能有差异，若a₁ > a₂，则Y_1j倾向于大于Y_2j；二是随机误差的存在，这一分析启发了如下的想法：找一个衡量全部Y_ij的变异的量：$$SS=\sum _{i=1}^k\sum _{j=1}^{n_i}(Y_{ij}-\tilde{Y}{)}^2，\tilde{Y}=\sum _{i=1}^k\sum _{j=1}^{n_i}{Y}_{ij}/n$$ SS愈大，表示Y_ij之间的差异越大
• 接下来把SS分为两部分，一部分表示随机误差的影响，记为SS_e；另一部分表示因素A的各水平理论平均值a_i不同带来的影响，记为SS_A
  关于SS_e，先固定一个i，此时对应的所有观测值Y_i1,Y_i2,…,Y_in，他们之间的差异与每个水平的理论平均值不等无关，取决于随机误差，反映这些观察值差异程度的量是${\sum }_{j=1}^{n_i}(Y_{ij}-\tilde{Y}{)}^2$，其中$${\tilde{Y}}_i=(Y_{i1}+Y_{i2}+...+Y_{in})/n_i，i=1,2,...,n$$
• ${\tilde{Y}}_i$可以视为对a_i的估计，将上述平方和做累加得：$$S{S}_e=\sum _{i=1}^k\sum _{j=1}^{n_i}(Y_{ij}-\widetilde{Y_i}{)}^2$$
• 可求得SS_A$$S{S}_A=SS-S{S}_e=\sum _{i=1}^k{n}_i(Y_i-\tilde{Y}{)}^2$$

因为${\tilde{Y}}_i$可以视为对a_i的估计，a_i的差异越大，${\tilde{Y}}_i$之间的差异也越大，所以SS_A可以用来衡量不同水平之间的差异程度。
在统计学上，通常称SS为总平方和、SS_A为因素A的平方和，SS_e为误差平方和，分解式SS = SS_A + SS_e为该模型的方差分析。

• 基于上面的分析我们可以得到假设检验的一个方法：当比值SS_A/SS_e大于某一给定界限时，否定H₀，不然就接受H₀，为了构造F分布的检验统计量，我们假定随机误差e_ij满足正态分布N(0, δ²)，同时我们也假定观察值Y_ij符合正态分布，此时记$$M{S}_A=S{S}_A/(k-1),M{S}_e=S{S}_e/(n-k)$$
• 当H₀成立时有$$M{S}_A/M{S}_e服从F_{k-1,n-k}$$
• 在给定显著性水平α时，H₀如下$$当M{S}_A/M{S}_e<=F_{k-1,n-k}(\alpha )时，接受H_0，不然就拒绝H_0$$
  MS_A和MS_e分别被称为因素A和随机误差的平均平方和，k-1 和n-k分别被称为这两个平方和的自由度，两者的自由度之和n-1为总平方和的自由度
  
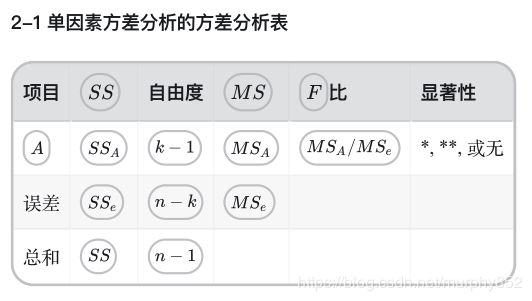
  我们一般把计算出来的F值（MS_A/MS_e）与$c_1=F_{k-1,n-k}(0.05)$和$c_2=F_{k-1,n-k}(0.01)$比较，若F > c₂，用**表示，表明A因素的效应是高度显著的，即在α = 0.01的显著性水平下，拒绝原假设，同理，c₂ < F < c₁用*表示，F > c₁时不显著

2.Python实现

from scipy import stats
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import warnings
import itertools
warnings.filterwarnings("ignore")

df2=pd.DataFrame()
df2['group']=list(itertools.repeat(-1.,9))+list(itertools.repeat(0.,9))+list(itertools.repeat(1.,9))

df2['noise_A']=0.0
for i in data['A'].unique():
    df2.loc[df2['group']==i,'noise_A']=data.loc[data['A']==i,['1','2','3']].values.flatten()
    
df2['noise_B']=0.0
for i in data['B'].unique():
    df2.loc[df2['group']==i,'noise_B']=data.loc[data['B']==i,['1','2','3']].values.flatten()  
    
df2['noise_C']=0.0
for i in data['C'].unique():
    df2.loc[df2['group']==i,'noise_C']=data.loc[data['C']==i,['1','2','3']].values.flatten()  
    
# for A
anova_reA= anova_lm(ols('noise_A~C(group)',data=df2[['group','noise_A']]).fit())
print(anova_reA)
#B
anova_reB= anova_lm(ols('noise_B~C(group)',data=df2[['group','noise_B']]).fit())
print(anova_reB)
#C
anova_reC= anova_lm(ols('noise_C~C(group)',data=df2[['group','noise_C']]).fit())
print(anova_reC)

双因素方差分析

1.推导过程

在很多情况下，只考虑一个指标对观察值的影响是远远不够的，这时就会用到多因素方差分析。

还是以田间实验的例子帮助理解推导过程。

• 我们假设有两个因素A，B，分别有k，l个水平，A的水平i与B的水平j的组合记为(i,j)，其试验结果记为Y_ij,i =1,…,k，j = 1,…,l，统计模型定为：$$Y_{ij}=\mu +a_i+b_j+e_{ij}，i=1,...,k，j=1,...,l$$
• 为解释这模型，首先把右边分成两部分：e_ij为随机误差，它包含了未加控制的因素（A、B以外的因素）及大量随机因素的影响，假定$$E(e_{ij})=0,0<Var(eij)={\delta }^2<\infty ，一切e_{ij}独立同分布$$
• 另一部分μ + a_i + b_j，它显示水平组合(i,j)的平均效应，它又可以分解为三部分：μ是总平均（一切水平组合效应的平均）， a_i表示由A的水平i带来的增加的部分，称为因素A的水平i的效应，b_j同理，调整μ的值，我们可以补充要求：$$a_1+a_2+...+a_k=0，b_1+b_2+...+b_l=0$$
• 约束条件给了a_i，b_j的意义一种更清晰的解释：a_i > 0 表示A的水平i的效应在A的全部水平的平均效应之上，a_i < 0则相反，另外这个约束条件也给了μ，a_i，b_j的一个适当的估计法：把Y_ij对一切i，j相加，则有$$\sum _{i=1}^k\sum _{j=1}^l{Y}_{ij}=kl\mu +\sum _{i=1}^k\sum _{j=1}^l{e}_{ij}$$
• 由上式得$$\tilde{Y}=\sum _{i=1}^k\sum _{j=1}^l{Y}_{ij}/kl$$是μ的一个无偏估计
• 另有$$\sum _{j=1}^l{Y}_{ij}=l\mu +la+\sum _{j=1}^l{e}_{ij}$$
• 于是，记$$\widetilde{Y_i}=\sum _{j=1}^l{Y}_{ij}/l，\widetilde{Y_j}=\sum _{i=1}^k{Y}_{ij}/k$$
• ${\tilde{Y}}_j$为μ + a_i的一个无偏估计，于是得到a_i的一个无偏估计为$$\widehat{a_i}=\widetilde{Y_i}-\tilde{Y}，i=1,...,k$$
• 同理$$\widehat{b_j}=\widetilde{Y_j}-\tilde{Y}，j=1,...,l$$
• 接下来把SS分为三部分，SS_A、SS_B、SS_e分别表示因素A、B和随机误差的影响。
• 假设$$H_{0A}：a_1=a_2=...=a_k=0$$和$$H_{0B}：b_1=b_2=...=b_k=0$$
• 得到$$SS=S{S}_A+SS+S{S}_e=l\sum _{i=1}^k({\tilde{Y}}_i-\tilde{Y}{)}^2+k\sum _{j=1}^l({\tilde{Y}}_j-\tilde{Y}{)}^2+\sum _{i=1}^k\sum _{j=1}^l(Y_{ij}-{\tilde{Y}}_i-{\tilde{Y}}_j+\tilde{Y}{)}^2$$
• 自由度
  SS_A自由度：k - 1
  SS_B自由度：l - 1
  总和自由度：kl - 1
  误差平方和自由度：(k - 1)(l - 1)
  

2.Python实现

dic_t2=[{'广告':'A1','价格':'B1','销量':276},{'广告':'A1','价格':'B2','销量':352},
       {'广告':'A1','价格':'B3','销量':178},{'广告':'A1','价格':'B4','销量':295},
       {'广告':'A1','价格':'B5','销量':273},{'广告':'A2','价格':'B1','销量':114},
       {'广告':'A2','价格':'B2','销量':176},{'广告':'A2','价格':'B3','销量':102},
       {'广告':'A2','价格':'B4','销量':155},{'广告':'A2','价格':'B5','销量':128},
       {'广告':'A3','价格':'B1','销量':364},{'广告':'A3','价格':'B2','销量':547},
       {'广告':'A3','价格':'B3','销量':288},{'广告':'A3','价格':'B4','销量':392},
       {'广告':'A3','价格':'B5','销量':378}]
df_t2=pd.DataFrame(dic_t2,columns=['广告','价格','销量'])
#无交互作用的双因素方差分析
def f_twoway(df_c,col_fac1,col_fac2,col_sta,interaction=False):
    df=df_c.copy()
    list_fac1=df[col_fac1].unique()
    list_fac2=df[col_fac2].unique()
    r=len(list_fac1)
    s=len(list_fac2)
    x_bar=df[col_sta].mean()
    list_Qa=[]
    list_Qb=[]
    for i in list_fac1:
        series_i=df[df[col_fac1]==i][col_sta]
        xi_bar=series_i.mean()
        list_Qa.append((xi_bar-x_bar)**2)
    for j in list_fac2:
        series_j=df[df[col_fac2]==j][col_sta]
        xj_bar=series_j.mean()
        list_Qb.append((xj_bar-x_bar)**2)
    Q=((df[col_sta]-x_bar)**2).sum()
    df_res=pd.DataFrame(columns=['方差来源','平方和','自由度','均方','F值','Sig.'])
    if interaction==False:
        Qa=s*sum(list_Qa)
        Qb=r*sum(list_Qb)
        Qw=Q-Qa-Qb
        Sa=Qa/(r-1)
        Sb=Qb/(s-1)
        Sw=Qw/((r-1)*(s-1))
        sig1=stats.f.sf(Sa/Sw,r-1,(r-1)*(s-1))
        sig2=stats.f.sf(Sb/Sw,s-1,(r-1)*(s-1))
        df_res['方差来源']=[col_fac1,col_fac2,'误差','总和']
        df_res['平方和']=[Qa,Qb,Qw,Q]
        df_res['自由度']=[r-1,s-1,(r-1)*(s-1),r*s-1]
        df_res['均方']=[Sa,Sb,Sw,'-']
        df_res['F值']=[Sa/Sw,Sb/Sw,'-','-']
        df_res['Sig.']=[sig1,sig2,'-','-']
        return df_res
    elif interaction==True:
        list_Qw=[]
        t=len(df[(df[col_fac1]==list_fac1[0]) & (df[col_fac2]==list_fac2[0])])
        for i in list_fac1:
            for j in list_fac2:
                series_ij=df[(df[col_fac1]==i) & (df[col_fac2]==j)][col_sta]
                list_Qw.append(((series_ij-series_ij.mean())**2).sum())
        Qa=s*t*sum(list_Qa)
        Qb=r*t*sum(list_Qb)
        Qw=sum(list_Qw)
        Qab=Q-Qa-Qb-Qw
        Sa=Qa/(r-1)
        Sb=Qb/(s-1)
        Sab=Qab/((r-1)*(s-1))
        Sw=Qw/(r*s*(t-1))
        sig1=stats.f.sf(Sa/Sw,r-1,r*s*(t-1))
        sig2=stats.f.sf(Sb/Sw,s-1,r*s*(t-1))
        sig3=stats.f.sf(Sab/Sw,(r-1)*(s-1),r*s*(t-1))
        df_res['方差来源']=[col_fac1,col_fac2,col_fac1+'*'+col_fac2,'误差','总和']
        df_res['平方和']=[Qa,Qb,Qab,Qw,Q]
        df_res['自由度']=[r-1,s-1,(r-1)*(s-1),r*s*(t-1),r*s*t-1]
        df_res['均方']=[Sa,Sb,Sab,Sw,'-']
        df_res['F值']=[Sa/Sw,Sb/Sw,Sab/Sw,'-','-']
        df_res['Sig.']=[sig1,sig2,sig3,'-','-']
        return df_res
    else:
        return 'interaction参数错误'
f_twoway(df_t2,'广告','价格','销量')

参考资料：
Python玩转数据分析——双因素方差分析