论文阅读-可迁移对抗样本攻击
我的博客已全部迁往个人博客站点:oukohou.wang,敬请前往~~
- paper:Transferable Adversarial Attacks for Image and Video Object Detection
Hello 大家好,本次带来的是针对目标检测的可迁移对抗样本攻击。
听起来好高大上的样子,其实就是对抗样本攻击,不过这次用在了目标检测上,然后加了个小trick, 使得攻击方法可以在两种目标检测方法上都奏效,所以就说是可迁移的。
具体如何呢?我们一一道来~~
1. 前情提要
众所周知,当前的目标检测模型有两类:proposal based models and regression based mod-els。其实就是一个是基于锚框,一个是直接回归。
然后作者分析了一波目前已存的针对目标检测的对抗样本攻击方法,大部分都是针对proposal-based models的:
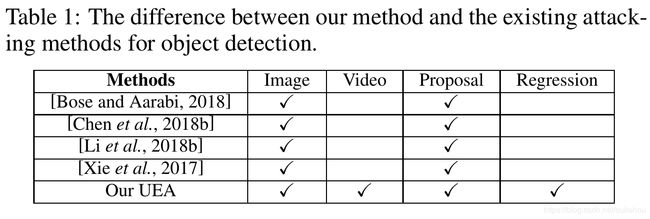
于是乎作者眼睛一转,计上心来:
不管你哪种方法,你总要有 feature map 的吧?那我把 feature map 也给攻击了,岂不就是一个大一统的攻击方法了?
好的,上面这句话就是全文的 文眼 了,下面我们看作者究竟使些什么手段。
2. UEA(Unified and Efficient Adversary)
怎么样,光看这个 UEA 的名字是不是也觉得很像大一统的意思?野心很大啊~~
模型框架结构如下:

具体来说,就是用 条件GAN(conditional GAN)来生成对抗样本,不过在其上多加了几个损失函数来监督生成器的生成效果。
第一个当然就是 L c G A N L_{cGAN} LcGAN:
L c G A N ( G , D ) = E I [ l o g D ( I ) ] + E I [ l o g ( 1 − D ( G ( I ) ) ) ] L_{cGAN}(G,D) = E_I[logD(I)]+E_I[log(1-D(G(I)))] LcGAN(G,D)=EI[logD(I)]+EI[log(1−D(G(I)))]
然后加了个 L 2 L_2 L2 loss:
L L 2 ( G ) = E I [ ∣ ∣ I − G ( I ) ∣ ∣ 2 ] L_{L_2}(G) = E_I[||I-G(I)||_2] LL2(G)=EI[∣∣I−G(I)∣∣2]
当然,只有这两个的话,就只是个单纯的复制网络了,肯定不行,还加了个 Adversarial examples for semantic segmentation and object detection
里用的 misclassify loss:
L D A G ( G ) = E I [ ∑ n = 1 N [ f l n ( X , t n ) − f l ^ n ( X , t n ) ] L_{DAG}(G) = E_I[\sum_{n=1}^N[f_{l_n}(X,t_n) - f_{\hat{l}_n}(X,t_n)] LDAG(G)=EI[n=1∑N[fln(X,tn)−fl^n(X,tn)]
式中, X X X 就是 feature map, τ = t 1 , t 2 , . . . , t N \tau = {t_1, t_2, ..., t_N} τ=t1,t2,...,tN 是 X X X 上的 proposal regions,阈值为 0.7, l n l_n ln 是 t n t_n tn 的
ground-truth label, l ^ n \hat{l}_n l^n 是从其他错误 labels 里随机取样的错误 label, f l n ( X , t n ) ∈ R C f_{l_n}(X,t_n)\in\mathbb{R}^{C} fln(X,tn)∈RC
则指 t n t_n tn 的 classification score vector (before softmax normalization)。
说到这里,如果你还没被绕晕的话,就会发现这个 misclassify loss 仅仅是针对 proposal based models 的,那前面说的针对 feature map 的攻击怎么实现的呢?
这就是下面这个 multi-scale attention feature loss 了:
L F e a ( G ) = E [ ∑ m = 1 M ∣ ∣ A m ∗ ( X m − R m ) ∣ ∣ 2 ] L_{Fea}(G) = E_[\sum_{m=1}^M||A_m*(X_m-R_m)||_2] LFea(G)=E[m=1∑M∣∣Am∗(Xm−Rm)∣∣2]
式中, X m X_m Xm 是 m 层的 feature map, R m R_m Rm 是随机定义的一个 feature map, A m A_m Am 是所谓的 attention weight。
于是乎,这最后一个 multi-scale attention feature loss 就实现了作者所说的 Unified and Efficient Adversary 了。
于是乎,最终的损失函数为:
L = L c G A N + α L L 2 + β L D A G + ϵ L F e a L= L_{cGAN} + \alpha L_{L_2} + \beta L_{DAG} + \epsilon L_{Fea} L=LcGAN+αLL2+βLDAG+ϵLFea
不消说, α , β , ϵ \alpha, \beta, \epsilon α,β,ϵ是权重系数, α = 0.05 \alpha =0.05 α=0.05, β = 1 \beta =1 β=1, ϵ = { 1 ∗ 1 0 − 4 , 2 ∗ 1 0 − 4 } \epsilon = \left \{ 1*10^{-4}, 2*10^{-4} \right \} ϵ={1∗10−4,2∗10−4}.
3. 大功告成
最后就是些对比图了,可想而知,作者用的生成模型,那么对抗样本的生成时间自然大大缩短;
同时又把 feature map 给改了,自然对两种检测模型都能奏效。
放两张图:
好啦,想看更多的图,敬请前往原 paper 观看~~
微信公众号:璇珠杂俎(也可搜索 oukohou),提供本站优质非技术博文~~
regards.


