Acm之最短路问题算法合集
最短路问题常见有以下这几种解法:
多源最短路: 1. Folyd (最容易实现)
单源最短路: 2. Dijkstra (用点进行松弛)(文字与图片来自啊哈算法)
3. Bellman-Ford (用边进行松弛)
4. spfa算法 (bellman-队列优化) (推荐)
5. Bfs (只有每一步的代价一样长的时候才适用)
6. A* (过于复杂,比赛几乎用不到)
1. Floyd解法 —— 会超时,这里也不讲解(对每两个点进行松弛操作)
啊哈算法的解释:https://www.cnblogs.com/ECJTUACM-873284962/p/6995648.html
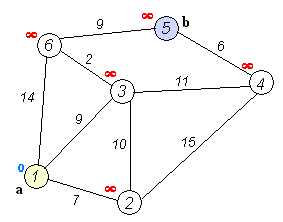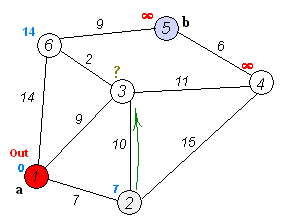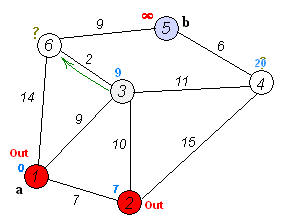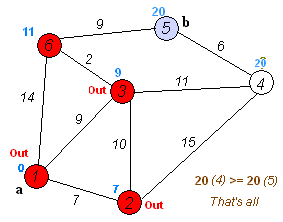
2. Dijkstra算法
准备工作: 用邻接矩阵map来储存 图,
用 dis来储存 起点到其余各顶点的初始路程,
算法流程:

代码实现步骤 1:
minn = 1e9;
for(int j = 0; j <= n; j++) //左手抓出 集合外的最小点
{
if(!visited[j] && dis[j] < minn) // 保证了在集合p 之外,抓取离起点最近的新点
{
minn = dis[j];
temp = j;
}
}
visited[temp] = 1; //( 之前图片中漏掉了) 抓取新点后应该将其标记为放入集合 P内, 即标记为旧点代码实现步骤 2:
if( map[temp][j] < 1e9 && dis[temp] + map[temp][j] < dis[j]) //确保有路,且,然后松弛
dis[j] = dis[temp] + map[temp][j];
代码实现步骤 3:
for(int j = 0; j <= n; j++) //借助 新点 对集合P内的每个元素(每个旧点) 进行松弛操作
if( map[temp][j] < 1e9 && dis[temp] + map[temp][j] < dis[j]) //确保有路,且,然后松弛
dis[j] = dis[temp] + map[temp][j];代码实现步骤 4:
for(int i = 0; i <= n; ++i) //这个循环只起到 次数的作用, 运行 n 次, 左手会抓 n 次, 会松弛完所有点
{
minn = 1e9;
for(int j = 0; j <= n; j++) //左手抓出 集合外的最小点
{
if(!visited[j] && dis[j] < minn)
{
minn = dis[j];
temp = j;
}
}
visited[temp] = 1; //放入 p 内
for(int j = 0; j <= n; j++) //用新点对集合内每个点进行松弛操作, 更新最短距离
if( map[temp][j] < 1e9 && dis[temp] + map[temp][j] < dis[j])
dis[j] = dis[temp] + map[temp][j];
}
完整代码:
void dijkstra()
{
for(int i = 0; i <=n; ++i)
dis[i] = map[0][i];
memset(visited, 0, sizeof(visited));
for(int i = 0; i <= n; ++i)
{
minn = 1e9;
for(int j = 0; j <= n; j++) //左手抓出 集合外的最小点
{
if(!visited[j] && dis[j] < minn)
{
minn = dis[j];
temp = j;
}
}
visited[temp] = 1;
for(int j = 0; j <= n; j++)
if( map[temp][j] < 1e9 && dis[temp] + map[temp][j] < dis[j])
dis[j] = dis[temp] + map[temp][j];
}
}松弛操作的通俗记忆: 新点绕路短则更
最后附上完整过程图:
3.Bellman-Ford 的队列优化 -- spfa(解决负边权)
这里我们不讲原版的bellman算法,直接讲解其优化,省事。直到太多反而容易混
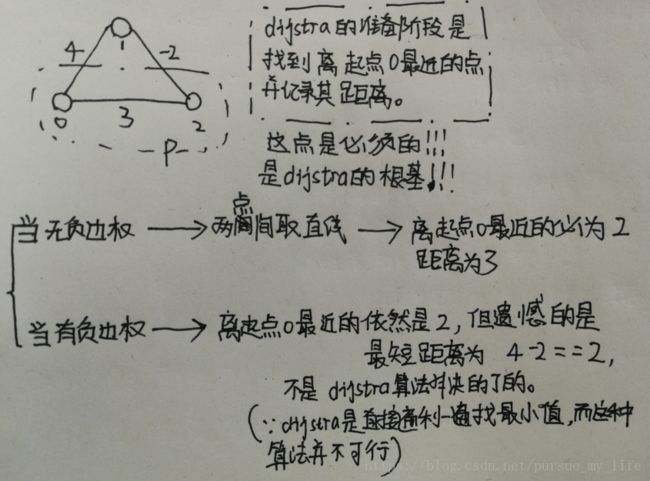
首先来很搞清楚负边权的问题
(一)为什么最短路问题会有负边权的存在?? 负边权的作用是什么??
(未完待续)
(二)Dijstra 为什么不能解决负边权???
由于第一点的选错,便会导致后面所有的最短路都算错。(Dp的子结构一层一层往上推)
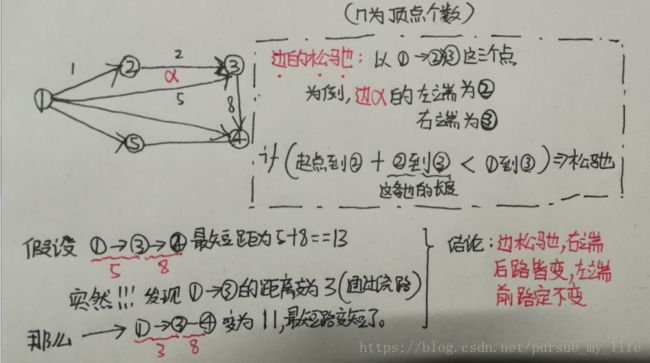
下面我们来讲解 Bellman-ford 的队列算法, 本质就是 DFS + bellman
我们可以看出当一条路劲上 起点到其中一个点的路劲变短(松弛)之后, 后面的每个节点到起点的距离都
要发生变化,而这个节点 之前 的节点都不用更新。(图中结论已给出)
所以,我们用DFS的方式进行遍历
准备阶段: 假设起点到所有点的距离是 无穷
(图中的 队列 写成了栈, 望海涵)
准备阶段的实现:
void init()
{
for(int i = 0; i < maxn; ++i)
for(int j = 0; j < maxn; ++j)
if(i == j) map[i][j] = 0;
else map[i][j] = inf;
memset(vis, false, sizeof(vis));
memset(money, false, sizeof(money));
for(int i = 0; i < maxn; ++i)
memset(cost[i], false, sizeof(cost[i]));
fill( dis, dis+maxn, inf);
}
代码实现步骤1:
que.push( s ); vis[s] = true; dis[s]= 0; int x = que.front(); que.pop(); vis[x] = false;
for(int i = 1; i <= n; ++i)
{
if(map[x][i] < inf)//insure had road
{
if( dis[x]/*pre*/ + map[x][i]/*edge*/ < dis[i]/*direct*/)
{
dis[i] = dis[x] + map[x][i];
money[i] = money[x] + cost[x][i];
if( !vis[i] )// if ont in queue, then push it in queue.
{
que.push( i );
vis[i] = true;
}
}
}
}void spfa()
{
que.push( s ); vis[s] = true; dis[s]= 0;
while( !que.empty() )
{
int x = que.front(); que.pop(); vis[x] = false;
for(int i = 1; i <= n; ++i)
{
if(map[x][i] < inf)//insure had road
{
if( dis[x]/*pre*/ + map[x][i]/*edge*/ < dis[i]/*direct*/)
{
dis[i] = dis[x] + map[x][i];
money[i] = money[x] + cost[x][i];
if( !vis[i] )// if ont in queue, then push it in queue.
{
que.push( i );
vis[i] = true;
}
}
}
}
}
}