R语言预测人口死亡率:用李·卡特模型、非线性模型进行平滑估计
原文链接:http://tecdat.cn/?p=13663
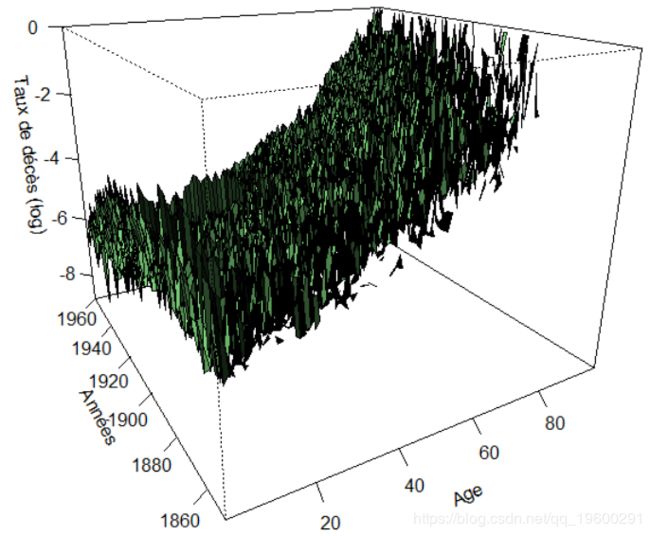
今天早上,我和同事一起分析死亡率。我们在研究人口数据集,可以观察到很多波动性。
我们得到这样的结果:
由于我们缺少一些数据,因此我们想使用一些广义非线性模型。因此,让我们看看如何获得死亡率曲面图的平滑估计。我们编写一些代码。
D=DEATH$Male
E=EXPO$Male
A=as.numeric(as.character(DEATH$Age))
Y=DEATH$Year
I=(A<100)
base=data.frame(D=D,E=E,Y=Y,A=A)
subbase=base[I,]
subbase=subbase[!is.na(subbase$A),]第一个想法可以是使用Poisson模型,其中死亡率是年龄和年份的平稳函数,类似于
![]() 可以使用
可以使用
persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")死亡率曲面图
还可以提取年份的平均值,这是![]() Lee-Carter模型中系数的解释
Lee-Carter模型中系数的解释
predAx=function(a) mean(predict(regbsp,newdata=data.frame(A=a,
Y=seq(min(subbase$Y),max(subbase$Y)),E=1)))
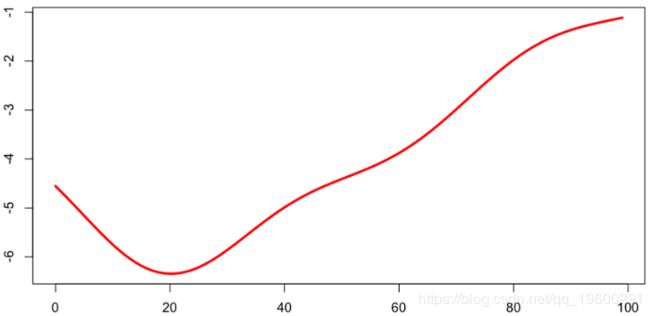
plot(seq(0,99),Vectorize(predAx)(seq(0,99)),col="red",lwd=3,type="l")我们有以下平滑的死亡率
回顾下李·卡特模型是
![]()
可以使用以下方法获得参数估计值
persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")粗略的死亡率曲面图是
有以下 ![]() 系数。
系数。
plot(seq(1,99),coefficients(regnp)[2:100],col="red",lwd=3,type="l")
这里我们有很多系数,但是,在较小的数据集上,我们具有更多的可变性。我们可以平滑李·卡特模型:
![]()
代码片段
persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")现在的死亡人数是
得出多年来随年龄变化的平均死亡率,
BpA=bs(seq(0,99),knots=knotsA,Boundary.knots=range(subbase$A),degre=3)
Ax=BpA%*%coefficients(regsp)[2:8]
plot(seq(0,99),Ax,col="red",lwd=3,type="l")
然后,我们可以使用样条函数的平滑参数,并查看对死亡率曲面的影响
persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")
热门文章
用r语言实现神经网络预测股票实例
八月 12, 2019 – 神经网络是一种基于现有数据创建预测的计算系统。在这个特定的例子中,我们的目标是开发一个神经网络来确定股票是否支付股息。
隐马尔科夫模型hmm在股市中的应用
2020年3月 –弄清楚何时开始或何时止损,调整风险和资金管理技巧,都取决于股市的当前状况。
机器学习精准销售时间序列预测
2020年4月 –对于零售行业来说,预测几乎是商业智能(BI)研究的终极问题。
r语言实现copula算法建模依赖性
2020年4月 –copula是将多变量分布函数与其边际分布函数耦合的函数,通常称为边缘。