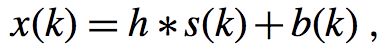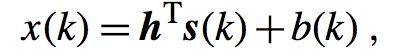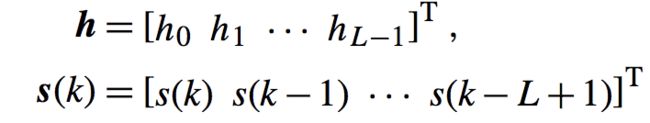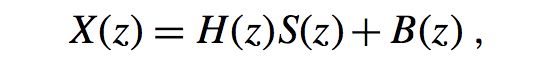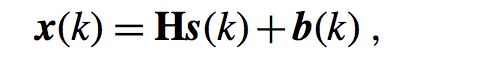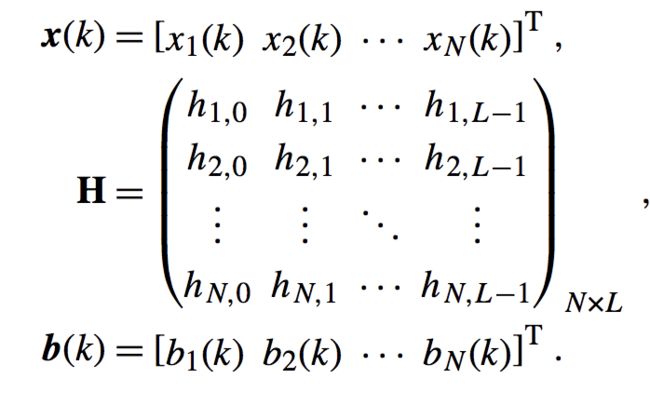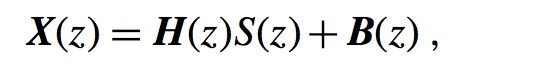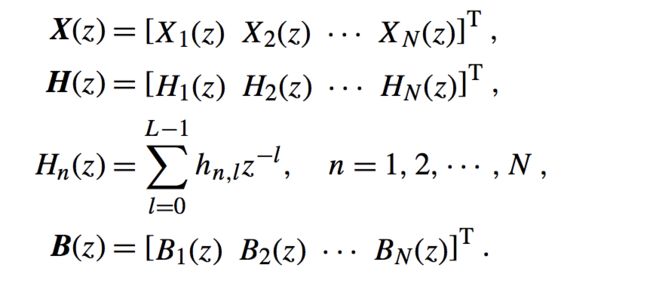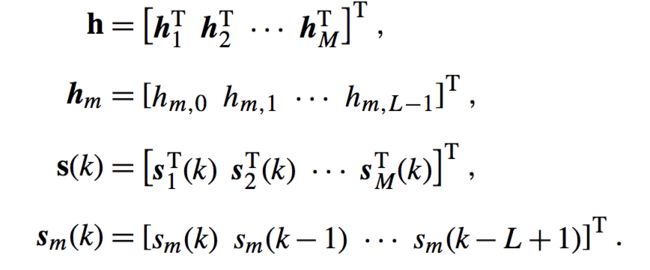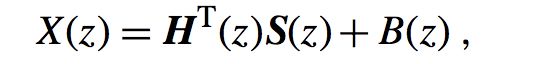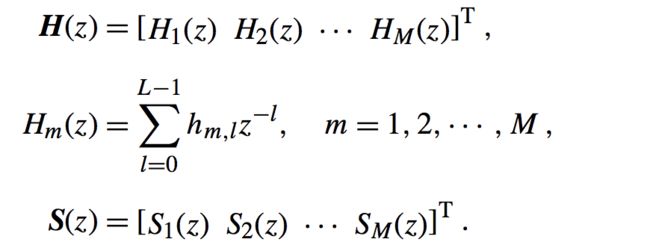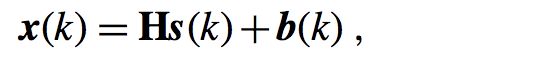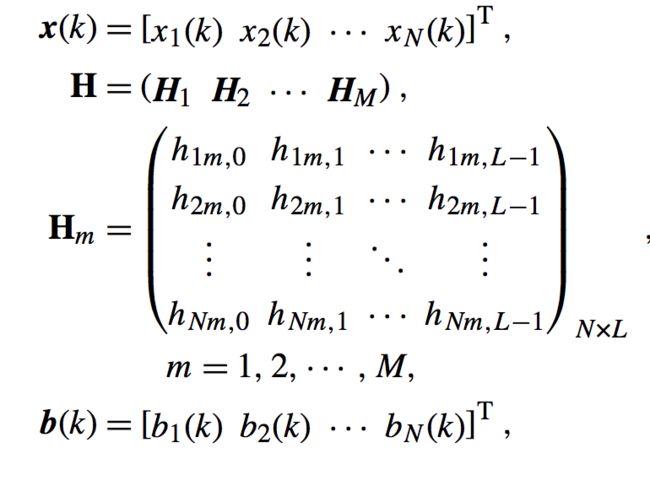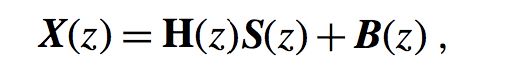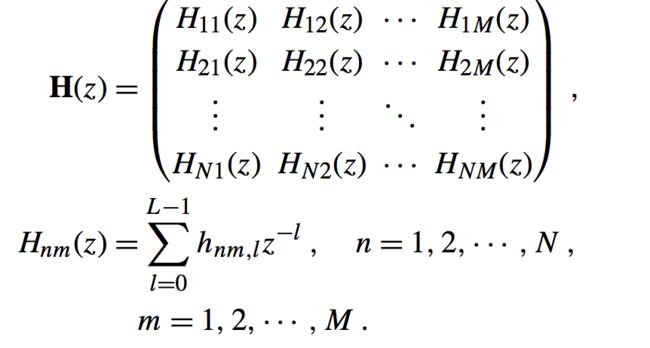维纳滤波器(一)
很久没有静下心来整理一下了,我很早之前就想做一个从Wiener 滤波器了开始讲的博客了,现在终于有了安静坐下来总结一下的理由。从这里开始入手我感觉是对这一年多时间的尊敬,我会从模型开始讲起,会把我从论文和书中的理解呈现出来,如果有时间,我会把我的代码放到我的git上,有兴趣的可以去看一下,不多说,进入主题。
1 信号模型
在很多的应用中,我们很多的工作都是对系统进行辨识(system iditification)。说白了就是一个假象模型里面缺少很多参数,我们需要通过各种算法把参数进行估计,然后得到系统。可能你会问为什么我需要个系统?这么说:假设你想对你录到的语音进行增强,也就是变相的减小噪声,那么这就是一个系统,我想我这么说大家应该会理解为什么需要一个系统。
那么在我们真正辨识系统之前,有个更主要的需要我们提前了解---信号模型。就是你对你的信号的组成进行建模,看其中都有哪些成分,比如包含噪声,回声等等,所以我们从信号模型开始入手。
1.1 SISO模型
这个模型其实指的就是单输入单输出模型。(这里深入想可能会有些绕,我仅仅是想对我的信号进行建模,怎么都出来输入输出了?那要看你怎么理解输入和输出,这里的输入指的是我们的原始信号比如你想增强的那个人的语音,输出指的是我们的观测信号也就是你录制的那个可能带有噪声的信号,这里的变化其实就是信号从原始经过何种变化最终我们得到了观测信号。)
现在我们给出此模型的公式:
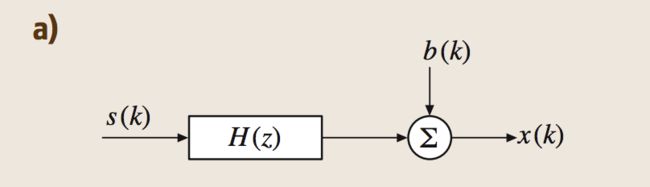
其系统图示如下:
这里的h是通道冲击响应,这里的*是卷积的意思(对于不明白卷积含义的,这里不做解释,可以自己去查阅资料)。s(k)是在k时刻的源信号,b(k)是附加的噪声。我们假设系统是线性的并且是时移不变的(这两点非常重要,因为我们一般信号处理的操作,都是为了后端提高识别率的,所以保证系统是线性的是必要的)。一般我们使用一个FIR滤波器而不是IIR滤波器来表示h。接下来我们给出SISO模型的向量形式:
其中:
(仅仅是变为了向量的形式,不过多解释)。其中T表示的是转置(行变列,列变行),L是我们滤波器的长度,一提到长度当然我们指的是在时域。这个长度在算法中很重要,是一个可调的重要参数,日后会遇到,我们先不展开说。
接下来我们使用Z变换,其实就是针对离散数据的傅里叶变换,我们的SISO模型变为如下:
其中各个大写字母是其各个信号的Z变换形式。同时从这里可以看出:时域的卷积可以巧妙的变化为频域的乘积。(很多算法选择在频域进行是从计算量出发的,不过不要以偏概全)。
1.2 SIMO模型
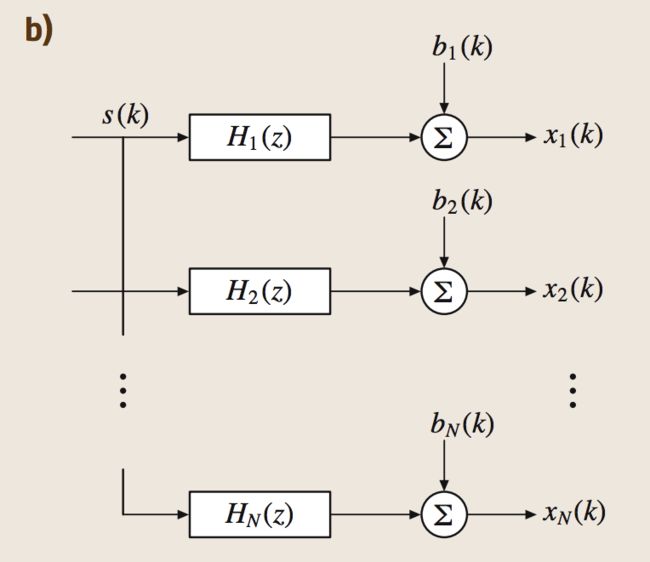
所谓SIMO就是单输出多输出的模型,可能有些人不理解,一个输入怎么会有多个输出呢?少年,发挥你追你女朋友的想象力,人有多大胆,地有多大产。假如一个人说话,多个麦克风采集,那是不是SIMO模型呢?不多说,我们给出关于SIMO的图解:
这里我们使用变量N来代表总共有N路输出。那么第n个输出的公式如下:
这里我们给的直接是向量的形式。如果上面理解了,下面我们要更见识更加麻烦和有难度的公式。我们刚才说了,上面的公式是求第n个,那么我如何拿公式来表示所有的N个输出呢?
其中:
这显然比我们SISO的式子要复杂,2D别慌,我能秀,呸呸,我能讲。首先我们看x,x变成了向量,并且是列向量,长度为N,不难理解,这是把N个输出都表示出来没毛病往下看H。H打眼一看感觉不是人看的,那么我们从矩阵乘法的角度推理:我们的x是一个列向量,要是使式子成立,我们的b也得是列项量表示各个输出夹杂的噪声,没毛病对的上。那么我们的Hs(k)也必然得是列向量。这也就是说一个N*L的H必须与一个L*1的s(k)进行想乘。那也就是我们H的各行与s(k)相乘然后得到最终结果。也就说用各个通道的通道冲击响应与源信号进行卷积然后得到N个通道的输出,完美解决,没有什么事情是一遍解决不了的,如果有,那就两遍。(聪明的小伙伴可能已经想到MIMO的时候的形式了)
同样我们仿照上面的形式,进行Z变换:
这里:
1.3 MISO模型
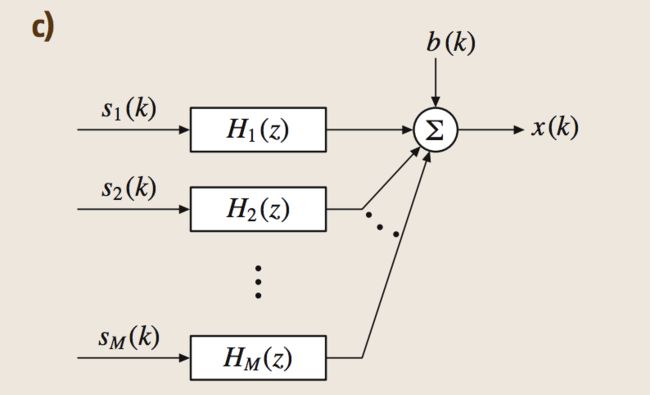
MISO模型就是多个输入一个输出,发挥想象力,没错多个人讲话一个麦克风采集最终形成了MISO模型。MISO模型的图解如下:
在最后我们看到了一个累加符号,那么明白了,其实就是把多个输出相加变为一个输出。那么我们的公式如下:
这里:
这里就有意思了,实话说我只能看懂第一部,对于使用矩阵相乘的方式(也就是第二个等号的位置)我个人认为书里这里是写错了的。理由如下:从第一个等号右边及其图解我们可以知道,最终我们得到的是一个时间点上的值。但是转化成矩阵后,我这里推解为:L*M的矩阵与M*L的矩阵的乘积是一个方阵L*L,并不是一个值,这与第一个式子右边的相互矛盾,所以我认为这里作者是写错了的。(如果哪位大V发现了我理解的漏洞欢迎在下面评论区指正,十分感谢)
根据上面我们得到MISO的Z变换如下:
那我从这里理解的话,是不是第一个等式第二个等号右边部分是hT与s(k)的卷积呢?猜测,仅仅是猜测。这里:
1.4 MIMO模型
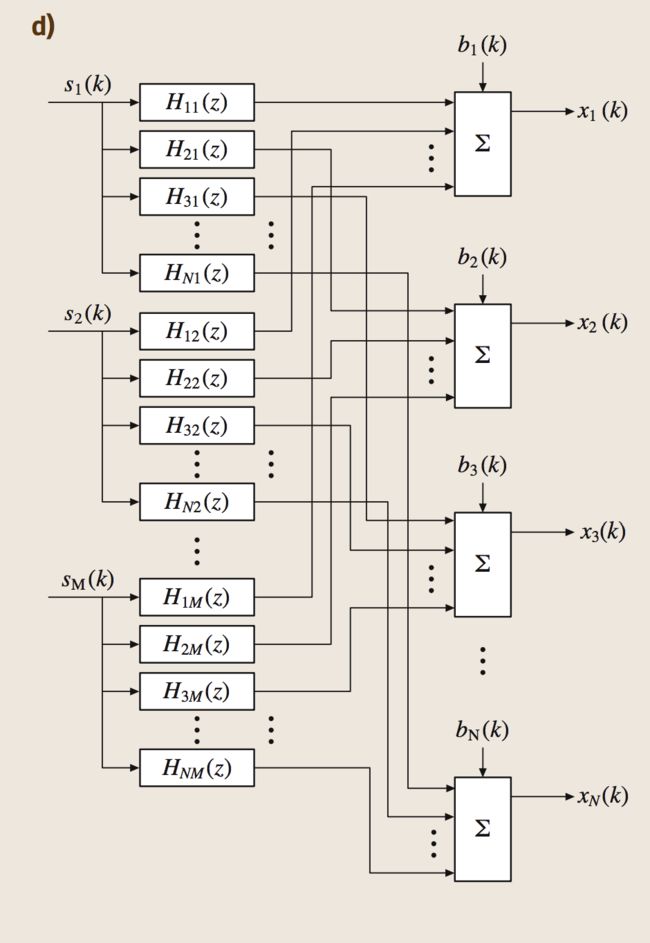
也就是著名的多输出多输出模型。实际场景为多个人说话,多个麦克风采集。MIMO的图解有些复杂,如下:
那么我们这里假设有M个输入,N个输出,k时刻我们得到公式如下:
其中:
这里有些麻烦,不过很容易理解,主要过程都是一一对应图解我不做详细推导,其中最关键的点就是:H是一个三维矩阵,N*L*M那么他和二维M*L相乘的话得到的应该是N*1,而我们的输出为N,所以能够对应。hnm表示从输入m到输出n的冲击响应。那么我们可以得到其Z变换如下:
其中:
我们可以看出来,MIMO模型是最通用的,其他三种都可以看做是其特殊情况。