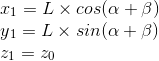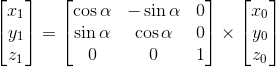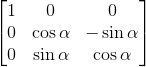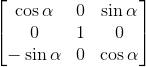【从理论到代码】旋转矩阵与欧拉角 一
本篇主要是结合odom坐标系与相机坐标系之间的转换，可以用于将odom数据与视觉slam进行融合时的位姿计算；
主要分为两部分，第一部分讲述旋转矩阵与欧拉角之间的转换；第二部分讲述如何将odom的位移和角度转换到相机坐标系下；
假设空间中的任意一点 
绕Z轴旋转了度，那么求旋转后的坐标，这里我直接给出自己的推导:
假设旋转之后的点为
，A点与X轴的夹角为beta，A点到原点的距离为L，那么我们可以得出以下几条式子：
按照三角函数的倍角公式展开代入L和的表达式化简之后有
写出矩阵形式有
尽管图示中仅仅表示的是旋转一个锐角的情形，但是我们推导中使用的是三角函数的基本定义来计算坐标的，因此当旋转的角度是任意角度（例如大于180度，导致A’点进入到第四象限）结论仍然是成立的。
同理可得其他两个轴的旋转矩阵如下
绕x轴旋转的alpha矩阵：
绕y轴旋转的alha矩阵：
由角度值转换成旋转矩阵的过程中需要注意两种情况，一种是绕固定轴旋转，一种是绕动态轴旋转。
以slam中的机器人的odom坐标系和相机坐标系为例：
这两种坐标系的关系图如下所示：（两个坐标系都符合右手法则）
以机器人的前进方向来说，当机器在向前方行进时，在坐标系中表示，即为向odom的x方向前进，向相机坐标系的z轴方向前进。
同理，odom坐标系的y轴正方向，与相机坐标系的x轴整方向差一个负号，表示成公式即为（不考虑平移）：
cam.x = -odom.y;
cam.y = -odom.z;
cam.z = odom.x;这种从odom坐标系到cam坐标系的关系 用固定轴和动态轴旋转方式表示分别如下：
对应在ORBSLAM中R矩阵的书写方式为Roc，即从odom坐标系旋转到cam坐标系
固定轴： 严格按照[x,y,z]的顺序：先绕odom坐标系的x轴逆时针旋转90度，再绕odom坐标系的y轴旋转0度，再绕odom坐标系的z轴旋转-90度；
动轴： 严格按照[z,y,x]的顺序：线绕odom的坐标系的z轴逆时针旋转-90度，再绕新odom的y轴旋转0度，再绕新odom的x轴逆时针旋转90度；
每一次旋转都会生成一个旋转矩阵，在拼接成最终的旋转矩阵时的顺序，都是Rotation = rotationZ*rotaionY*rotaionX;
因此，最后的R= [0, 0, 1; -1, 0, 0; 0,-1,0]
用Eigen来生成这个矩阵就是： (这里需要注意，在Eigen中传入的值是弧度值，而非角度值，所以要将-90 度转换为 -90.0*M_PI/180)
Eigen::Vector3d xyztheta(-90.0*M_PI/180, 0 ,-90*M_PI/180);
Eigen::Matrix Reigen;
Reigen = Eigen::AngleAxisd(xyzangles[2],Eigen::Vector3d::UnitZ()) *
Eigen::AngleAxisd(xyzangles[1],Eigen::Vector3d::UnitY())*
Eigen::AngleAxisd(xyzangles[0],Eigen::Vector3d::UnitX()); 这样计算出来的旋转矩阵
同理，如果已知旋转矩阵，想要转换成物体旋转各个表示方法之间的转换举例：
以cam1 为参考， 其R矩阵为单位阵， cam2相对与cam1之间的旋转矩阵为RotationMatrix，如下：
RotationMatrix << 0.539026 ,- 0.0785835, 0.838615,
0.0609289 ,0.996668, 0.0542316,
- 0.840082, 0.0218637, 0.542018;
Eigen::Vector3d euler_angles=RotationMatrix.eulerAngles(2,1,0);
std::cout << "yaw(Z) pitch(Y) roll(X)=\n" << euler_angles.transpose() << std::endl;将旋转矩阵转换成为欧拉角之后 yaw(Z) pitch(Y) roll(X)=0.112557 0.997435 0.0403156
这三个数分别代表了cam2绕cam1的各个轴之间的旋转弧度值，其范围为-Π