机器学习-白板推导 P4_3 (线性判别分析)
机器学习-白板推导 P4_3
- 线性判别分析(Fisher判别分析)
- 数据定义
- 思想
- 推导
- 目标函数
线性判别分析(Fisher判别分析)
数据定义
X = [ x 1 x 2 . . . x N ] T = [ x 1 T x 2 T ⋮ x N T ] = [ x 11 x 12 . . . x 1 p x 21 x 22 . . . x 2 p ⋮ ⋮ ⋱ ⋮ x N 1 x N 2 . . . x N p ] N ∗ p Y = [ y 1 y 2 ⋮ y N ] N ∗ 1 X=\begin{bmatrix} x_1 & x_2 &...& x_N \end{bmatrix}^T=\begin{bmatrix} x_1^T \\ x_2^T \\\vdots\\ x_N^T \end{bmatrix} = \begin{bmatrix} x_{11} & x_{12} &...& x_{1p} \\ x_{21} & x_{22} &...& x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N1} & x_{N2} &...& x_{Np} \\ \end{bmatrix}_{N*p}\qquad Y=\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \end{bmatrix}_{N*1} X=[x1x2...xN]T=⎣⎢⎢⎢⎡x1Tx2T⋮xNT⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡x11x21⋮xN1x12x22⋮xN2......⋱...x1px2p⋮xNp⎦⎥⎥⎥⎤N∗pY=⎣⎢⎢⎢⎡y1y2⋮yN⎦⎥⎥⎥⎤N∗1
{ ( x i , y i ) } i = 1 N , x i ∈ R p , y i ∈ { + 1 , − 1 } \lbrace(x_i,y_i) \rbrace_{i=1}^N, \quad x_i \in R^p, \quad y_i \in \lbrace +1,-1 \rbrace {(xi,yi)}i=1N,xi∈Rp,yi∈{+1,−1}
x c 1 = { x i ∣ y i = + 1 } x c 2 = { x i ∣ y i = − 1 } x_{c_1}=\lbrace x_i |y_i = +1 \rbrace \quad x_{c_2}=\lbrace x_i |y_i = -1 \rbrace xc1={xi∣yi=+1}xc2={xi∣yi=−1}
∣ x c 1 ∣ = N 1 , ∣ x c 2 ∣ = N 2 , N 1 + N 2 = N |x_{c_1}|=N_1, \quad |x_{c_2}|=N_2, \quad N_1+N_2=N ∣xc1∣=N1,∣xc2∣=N2,N1+N2=N
思想
类内小,类间大
降维的思想来分类,找到合适的投影方向
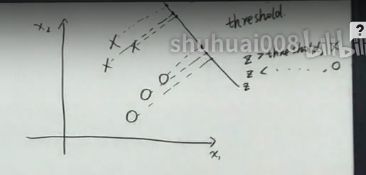
投影方向为 w T x w^Tx wTx的方向
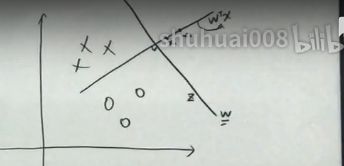
x i x_i xi在 w w w方向上的投影是多少?
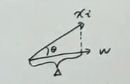
设: ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1
x i . w = ∣ x i ∣ ∣ w ∣ . c o s θ = ∣ x i ∣ c o s θ = Δ x_i.w=|x_i||w|.cos\theta=|x_i|cos\theta=\Delta xi.w=∣xi∣∣w∣.cosθ=∣xi∣cosθ=Δ
推导
定义:
z i = w T x i z_i=w^Tx_i zi=wTxi
整体均值 z ‾ \overline{z} z ,方差 S z S_z Sz
z ‾ = 1 N ∑ i = 1 N z i = 1 N ∑ i = 1 N w T x i \overline{z} = \frac{1}{N} \sum_{i=1}^Nz_i=\frac{1}{N} \sum_{i=1}^Nw^Tx_i z=N1∑i=1Nzi=N1∑i=1NwTxi
S z = 1 N ∑ i = 1 N ( z i − z ‾ ) ( z i − z ‾ ) T = 1 N ∑ i = 1 N ( w T x i − z ‾ ) ( w T x i − z ‾ ) T S_z=\frac{1}{N} \sum_{i=1}^N(z_i - \overline{z})(z_i - \overline{z})^T=\frac{1}{N} \sum_{i=1}^N(w^Tx_i- \overline{z})(w^Tx_i - \overline{z})^T Sz=N1∑i=1N(zi−z)(zi−z)T=N1∑i=1N(wTxi−z)(wTxi−z)T
c 1 c_1 c1的均值 z 1 ‾ \overline{z_1} z1 ,方差 S 1 S_1 S1
z 1 ‾ = 1 N 1 ∑ i = 1 N 1 w T x i \overline {z_1} =\frac{1}{N_1} \sum_{i=1}^{N_1} w^Tx_i z1=N11∑i=1N1wTxi
S 1 = 1 N 1 ∑ i = 1 N 1 ( w T x i − z 1 ‾ ) ( w T x i − z 1 ‾ ) T S_1 =\frac{1}{N_1} \sum_{i=1}^{N_1}(w^Tx_i- \overline{z_1})(w^Tx_i - \overline{z_1})^T S1=N11∑i=1N1(wTxi−z1)(wTxi−z1)T
c 2 c_2 c2的均值 z 2 ‾ \overline{z_2} z2 ,方差 S 2 S_2 S2
z 2 ‾ = 1 N 2 ∑ i = 1 N 2 w T x i \overline {z_2} =\frac{1}{N_2} \sum_{i=1}^{N_2} w^Tx_i z2=N21∑i=1N2wTxi
S 2 = 1 N 2 ∑ i = 1 N 2 ( w T x i − z 2 ‾ ) ( w T x i − z 2 ‾ ) T S_2 =\frac{1}{N_2} \sum_{i=1}^{N_2}(w^Tx_i- \overline{z_2})(w^Tx_i - \overline{z_2})^T S2=N21∑i=1N2(wTxi−z2)(wTxi−z2)T
目标函数
类间: ( z 1 ‾ − z 2 ‾ ) 2 (\overline {z_1} - \overline {z_2})^2 (z1−z2)2
类内: S 1 + S 2 S_1+S_2 S1+S2
J ( w ) = ( z 1 ‾ − z 2 ‾ ) 2 S 1 + S 2 J(w)=\frac{(\overline {z_1} - \overline {z_2})^2}{S_1+S_2} J(w)=S1+S2(z1−z2)2
w ^ = a r g max w J ( w ) \hat{w}=arg \max_w J(w) w^=argmaxwJ(w)
( z 1 ‾ − z 2 ‾ ) 2 = ( 1 N 1 ∑ i = 1 N 1 w T x i − 1 N 2 ∑ i = 1 N 2 w T x i ) 2 = ( w T ( 1 N 1 ∑ i = 1 N 1 x i − 1 N 2 ∑ i = 1 N 2 x i ) ) 2 = ( w T ( x c 1 ‾ − x c 2 ‾ ) ) 2 = w T ( x c 1 ‾ − x c 2 ‾ ) ( x c 1 ‾ − x c 2 ‾ ) T w \begin{aligned} (\overline {z_1} - \overline {z_2})^2 &=\left(\frac{1}{N_1} \sum_{i=1}^{N_1} w^Tx_i - \frac{1}{N_2} \sum_{i=1}^{N_2} w^Tx_i \right)^2 \\ &=\left( w^T\left( \frac{1}{N_1} \sum_{i=1}^{N_1} x_i - \frac{1}{N_2} \sum_{i=1}^{N_2} x_i \right) \right)^2 \\ &=\left(w^T\left( \overline{x_{c_1}} - \overline{x_{c_2}}\right) \right)^2 \\ &= w^T( \overline{x_{c_1}} - \overline{x_{c_2}}) ( \overline{x_{c_1}} - \overline{x_{c_2}}) ^Tw \end{aligned} (z1−z2)2=(N11i=1∑N1wTxi−N21i=1∑N2wTxi)2=(wT(N11i=1∑N1xi−N21i=1∑N2xi))2=(wT(xc1−xc2))2=wT(xc1−xc2)(xc1−xc2)Tw
S 1 = 1 N 1 ∑ i = 1 N 1 ( w T x i − z 1 ‾ ) ( w T x i − z 1 ‾ ) T = 1 N 1 ∑ i = 1 N 1 w T ( x i − x c 1 ‾ ) ( x i − x c 1 ‾ ) T w = w T ( 1 N 1 ∑ i = 1 N 1 ( x i − x c 1 ‾ ) ( x i − x c 1 ‾ ) T ) w = w T S c 1 w \begin{aligned} S_1 &= \frac{1}{N_1} \sum_{i=1}^{N_1}(w^Tx_i- \overline{z_1})(w^Tx_i - \overline{z_1})^T \\ &= \frac{1}{N_1} \sum_{i=1}^{N_1} w^T(x_i- \overline{x_{c_1}})(x_i- \overline{x_{c_1}})^Tw \\ &=w^T \left( \frac{1}{N_1} \sum_{i=1}^{N_1} (x_i- \overline{x_{c_1}})(x_i- \overline{x_{c_1}})^T \right) w \\ &= w^T S_{c_1}w \end{aligned} S1=N11i=1∑N1(wTxi−z1)(wTxi−z1)T=N11i=1∑N1wT(xi−xc1)(xi−xc1)Tw=wT(N11i=1∑N1(xi−xc1)(xi−xc1)T)w=wTSc1w
S 1 + S 2 = W T S c 1 W + W T S c 2 W = W T ( S c 1 + S c 2 ) W S_1+S_2=W^T S_{c_1}W+W^T S_{c_2}W=W^T (S_{c_1}+S_{c_2})W S1+S2=WTSc1W+WTSc2W=WT(Sc1+Sc2)W
J ( w ) = w T ( x c 1 ‾ − x c 2 ‾ ) ( x c 1 ‾ − x c 2 ‾ ) T w w T ( S c 1 + S c 2 ) w J(w)=\frac{ w^T( \overline{x_{c_1}} - \overline{x_{c_2}}) ( \overline{x_{c_1}} - \overline{x_{c_2}}) ^Tw}{w^T (S_{c_1}+S_{c_2})w} J(w)=wT(Sc1+Sc2)wwT(xc1−xc2)(xc1−xc2)Tw
定义:
S b = ( x c 1 ‾ − x c 2 ‾ ) ( x c 1 ‾ − x c 2 ‾ ) T S_b=( \overline{x_{c_1}} - \overline{x_{c_2}}) ( \overline{x_{c_1}} - \overline{x_{c_2}}) ^T Sb=(xc1−xc2)(xc1−xc2)T b e t w e e n − c l a s s \quad between-class\quad between−class类间方差 S b ∈ R p ∗ p S_b \in R^{p*p} Sb∈Rp∗p
S w = ( S c 1 + S c 2 ) S_w=(S_{c_1}+S_{c_2}) Sw=(Sc1+Sc2) w i t h i n − c l a s s \quad within-class\quad within−class类内方差 S w ∈ R p ∗ p S_w \in R^{p*p} Sw∈Rp∗p
J ( w ) = w T S b w w T S w w = w T S b w ( w T S w w ) − 1 J(w)=\frac{ w^TS_bw}{w^TS_ww}= w^TS_bw(w^TS_ww)^{-1} J(w)=wTSwwwTSbw=wTSbw(wTSww)−1
∂ J ( w ) ∂ w = 2 S b w ( w T S w w ) − 1 + w T S b w . ( − 1 ) ( w T S w w ) − 2 . 2 S w w = 0 \frac{\partial J(w)}{\partial w} = 2S_bw(w^TS_ww)^{-1} + w^TS_bw.(-1)(w^TS_ww)^{-2}.2S_ww=0 ∂w∂J(w)=2Sbw(wTSww)−1+wTSbw.(−1)(wTSww)−2.2Sww=0
S b w ( w T S w w ) − w T S b w S w w = 0 S_bw(w^TS_ww)-w^TS_bwS_ww=0 Sbw(wTSww)−wTSbwSww=0
S b w ( w T S w w ) = w T S b w S w w S_bw(w^TS_ww) = w^TS_bwS_ww Sbw(wTSww)=wTSbwSww
因为: w T S w w ∈ R ( 1 ∗ p ) ∗ ( p ∗ p ) ∗ ( p ∗ 1 ) = 1 w^TS_ww \in R^{(1*p)*(p*p)*(p*1)=1} wTSww∈R(1∗p)∗(p∗p)∗(p∗1)=1为一维数据,同理 w T S b w w^TS_bw wTSbw
所以: S w w = S b w ( w T S w w ) w T S b w . S b . w S_ww=\frac{S_bw(w^TS_ww)}{w^TS_bw}.S_b.w Sww=wTSbwSbw(wTSww).Sb.w
再次我们只关心 w w w的方向,因为大小可以任意缩放
w = S b w ( w T S w w ) w T S b w . S w − 1 . S b . w ∝ S w − 1 . S b . w = S w − 1 ( x c 1 ‾ − x c 2 ‾ ) ( x c 1 ‾ − x c 2 ‾ ) T . w w=\frac{S_bw(w^TS_ww)}{w^TS_bw}.S_w^{-1}.S_b.w \propto S_w^{-1}.S_b.w=S_w^{-1}(\overline{x_{c_1}}-\overline{x_{c_2}})(\overline{x_{c_1}}-\overline{x_{c_2}})^T.w w=wTSbwSbw(wTSww).Sw−1.Sb.w∝Sw−1.Sb.w=Sw−1(xc1−xc2)(xc1−xc2)T.w
因为: ( x c 1 ‾ − x c 2 ‾ ) T . w ∈ R ( 1 ∗ p ) ∗ ( p ∗ 1 ) = 1 (\overline{x_{c_1}}-\overline{x_{c_2}})^T.w \in R^{(1*p)*(p*1)=1} (xc1−xc2)T.w∈R(1∗p)∗(p∗1)=1为一维数据
w ∝ S w − 1 ( x c 1 ‾ − x c 2 ‾ ) w \propto S_w^{-1}(\overline{x_{c_1}}-\overline{x_{c_2}}) w∝Sw−1(xc1−xc2)
如果 S w − 1 S_w^{-1} Sw−1为对消矩阵,各向同性 S w − 1 ∝ I S_w^{-1} \propto I Sw−1∝I
w ∝ ( x c 1 ‾ − x c 2 ‾ ) w \propto (\overline{x_{c_1}}-\overline{x_{c_2}}) w∝(xc1−xc2)