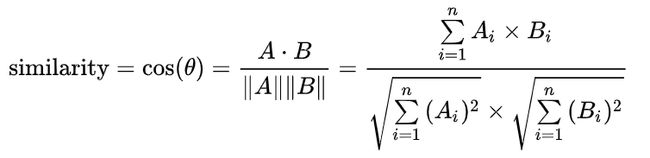词向量余弦算法计算文本相似度
计算文本相似度有多种方式,这里简单介绍一下其中的一种:词向量余弦。
词向量余弦
词向量余弦算法,是将文本作为一个多维空间的向量,计算两个文本的相识度即计算判断两个向量在这个多维空间中的方向是否是一样的。而这个多维空间的构成是通过将文本进行分词,每个分词代表空间的一个维度。
下面通过例子来说明多维空间的构成即词向量问题。比如要计算如下两个短文本的相识度:
文本一:天气预报说,明天会下雨,你明天早上去上班的时候记得带上伞。
文本二:你明天早上去上班的时候记得带上伞,天气预报说的可能会下雨。
首先我们利用某种分词方法将文本进行分词,如下:
这里不考虑标点符号,当然也可以涵盖
文本一分词:[天气 预报 说 明天 会 下雨 你 明天 早上 去 上班 的 时候 记 得 带 上 伞]
文本二分词:[你 明天 早上 去 上班 的 时候 记 得 带 上 伞 天气 预报 说 的 可能会 下 雨]
多维空间的词集合如下:
[天气 你 的 带 可能会 雨 上班 上 下 早上 时候 记 预报 说 明天 下雨 得 会 去 伞]
这是便可以得出连个文本在这个词集合构建的多维空间的词向量。
文本一的词向量:[1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1 ]
文本二的词向量:[1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1]
词向量得到了,这是便可以根据词向量余弦的公式计算出相似度值了,公式如下:
计算出的相似度值为: similarity = 0.8295150620062532
由余弦定理可知,cosine值的范围为[0,1],越趋近于1时两个向量的夹角越小,也代表两个文本越相似,
代码实现
这里用java实现词向量余弦算法,用一个矩阵来保存词向量的各维度的值。
public static double cosine(List<String> originWord, List<String> targetWord) {
Map<String, int[]> wordDict = new HashMap<>();
originWord.forEach(word -> {
if (!wordDict.containsKey(word)) {
int[] value = new int[2];
value[0] = 1;
wordDict.put(word, value);
} else {
wordDict.get(word)[0] += 1;
}
});
targetWord.forEach(word -> {
if (!wordDict.containsKey(word)) {
int[] value = new int[2];
value[1] = 1;
wordDict.put(word, value);
} else {
wordDict.get(word)[1] += 1;
}
});
double dictNum = 0, originNum = 0, desNum = 0;
for (Map.Entry<String, int[]> entry : wordDict.entrySet()) {
int origin = entry.getValue()[0];
int des = entry.getValue()[1];
originNum += origin * origin;
desNum += des * des;
dictNum += origin * des;
}
return dictNum / Math.sqrt(originNum * desNum);
}
案例代码
案例代码地址:https://github.com/lazycece/cosine-similar