Focal Loss for Dense Object Detection论文详解
《Focal Loss for Dense Object Detection》发表于ICCV2017
代码地址:
caffe2实现:https://github.com/facebookresearch/Detectron
keras实现:https://github.com/fizyr/keras-retinanet
文章思路:作者思考,目前two-stage的检测方法能够达到较高的精度,而one-stage虽然速度快,但是精度却达不到two-stage的效果。作者认为原因是在one-stage的训练过程中正负样本的不平衡造成的。对于一幅图像来说,一般有 1 0 4 − 1 0 5 10^4 - 10^5 104−105个候选区域,但是至少非常少的候选区域包含待检测物体。这种正负样本极度不平衡的情况下会导致两个问题:
- 训练效率低,大部分易于分类的负样本对模型的训练没有很大的指导意义
- 大量的易分类负样本加入训练,导致训练出来的效果不好,容易收到这部分样本的影响
因此,本文提出focal loss这种改进的交叉熵loss来解决样本不均衡带来的问题,又因为本文小改了一下网络结构,将新的网络结构称为retinanet,所以本文有人也称为retinanet。但是文章说明,本文的重点是提出一个有效的loss,而不是网络。
下面将按照本人一贯的解读习惯,先介绍一下网络结构,然后介绍focal loss
一、网络结构
简单来说本文采用的网络是resnet作为主干网络,网络框架采用的是FPN的结构,最后将FPN得到的各层feature map(P3-P7)都加上两个分支,一个用于回归框一个用于得到物体的类别。基本的网络结构如下图所示:
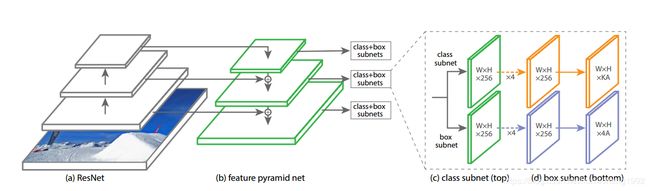
这里还要多解释两句P3-P7这几个feature map的来源。因为采用的backbone为resnet,对于resnet几个阶段的feature,重复利用C3-C5这几个feature。P6就是C5通过 3 × 3 3\times 3 3×3 stride-2的卷积得到,P7为P6经过ReLU函数后在经过 3 × 3 3\times 3 3×3 stride-2的卷积得到。其它几层类似于FPN。
1.1 Anchors
虽然是one-stage,但还是使用anchor的方式都物体进行检测的,所以还有一些关于anchor的参数设置。
因为使用了FPN中的P3-P7层的featuremap,每层feature的大小不一致,所以anchors的大小也不一致,对应的大小为 3 2 2 , 6 4 2 , 12 8 2 , 25 6 2 , 51 2 2 32^2, 64^2, 128^2, 256^2, 512^2 322,642,1282,2562,5122。而对于每一层的anchor,每个anchor的长宽比为{1:2, 1:1, 2:1},每个anchor大小在上述的基础大小上进行缩放,缩放比例为 2 0 , 2 1 / 3 , 2 2 / 3 {2^0, 2^{1/3}, 2^{2/3}} 20,21/3,22/3。所以在每个featuremap上每个点都对应9个不同的anchor,而每个不同的featuremap对应的anchor面积大小也是不一样的。这部分类似与fasterrcnn
的设计,不太理解的看看fasterrcnn详解。
至于正负训练样本的选择,anchor与gt框的IoU大于0.5定为正样本,IoU在[0,0.4)之间的定为负样本,其他的anchor则忽略不参与训练。
1.2 输出分支(Classification Subnet 和 Box Regression Subnet)
分类分支(Classification Subnet)
对于上述得到的P3-P7的feature,每个feature都经过4个 3 × 3 3\times 3 3×3的卷积层,每个卷积之后都进行relu的激活,最后在经过一个 3 × 3 3\times 3 3×3的卷积得到9×K个通道,对应每个anchor对应的类别。
回归分支(Box Regression Subnet)
这个分支和上面的分类分支是平行的,也就是他们是独立的。结构和上面分支基本一样,只是输出维度不同,这个分支输出9*4个通道,对应每个anchor的四个回归值。
二、Focal Loss
这个是本文的一大创新,也是重点内容,它是对cross entropy loss的一种改进。
下面先看看一个二分类的交叉熵表示
C E ( p , y ) = { − l o g ( p ) i f y = 1 − l o g ( 1 − p ) o t h e r w i s e CE(p,y)=\left\{\begin{aligned}-log(p) \quad if \quad y=1 \\ -log(1-p) \quad otherwise \end{aligned}\right. CE(p,y)={−log(p)ify=1−log(1−p)otherwise
为了方便定义 p t p_t pt:
p t = { p i f y = 1 1 − p o t h e r w i s e , p_t=\left\{\begin{aligned} p \quad if \quad y=1 \\ 1-p \quad otherwise, \end{aligned}\right. pt={pify=11−potherwise,
这样可以得到 C E ( p , y ) = C E ( p t ) = − l o g ( p t ) CE(p,y)=CE(p_t)=-log(p_t) CE(p,y)=CE(pt)=−log(pt)
这种loss的计算方法在有大量易分类的样本中,难分类的样本容易本起不到决定性的作用。
为了平衡正负样本的作用,将上述loss改为:
C E ( p t ) = − α t l o g ( p t ) CE(p_t)=-\alpha_t log(p_t) CE(pt)=−αtlog(pt)
上式中的 α t \alpha_t αt为一个0-1之间的数,一般取于类别频率成反比的数。
上面改进能够起到平衡样本的作用,但是并没有对一些容易分类的样本做处理,我们不仅希望平衡样本,而且希望将易分类的样本提供的loss比重减小,所以提出下面的式子:
F L ( p t ) = − ( 1 − p t ) γ l o g ( p t ) FL(p_t)=-(1-p_t)^\gamma log(p_t) FL(pt)=−(1−pt)γlog(pt)
其中 γ \gamma γ为大于等于0的一个超参数,下图为将 γ \gamma γ取值为[0,5]的一个可视化曲线。
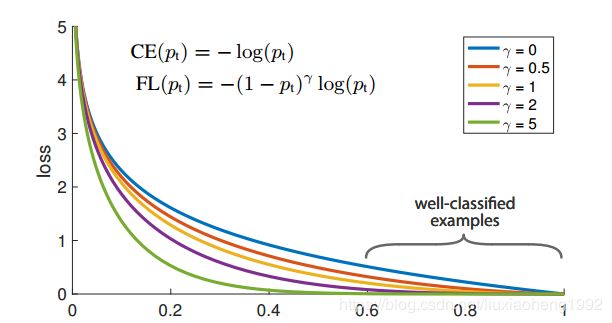
对于上面的式子我们可以看出两点:
- 当一个样本被错分类后,且 p t p_t pt较小,则前面因子接近于1,loss几乎没影响
- 当一个样本 p t p_t pt接近于1,因子接近0,这样导致易分类样本loss权重减小,从而达到给易分类样本loss降权的目的。
最后为了平衡样本在上面的loss前加上平衡因子,最终focalloss形式如下:
F L ( p t ) = − α t ( 1 − p t ) γ l o g ( p t ) FL(p_t)=-\alpha_t(1-p_t)^\gamma log(p_t) FL(pt)=−αt(1−pt)γlog(pt)
在文章的实验中, γ = 2 , α = 0.25 \gamma=2, \alpha=0.25 γ=2,α=0.25达到最好的效果。
到这里这篇文章就介绍完了。
欢迎加入Object Detection交流,群聊号码:910457072