李宏毅学习笔记27.Unsupervised Learning.05: Deep Generative Model (Part II)
文章目录
- Why VAE?
- 先看下普通AE
- 再看看VAE咋整的。
- 科学解释
- GMM Gaussian Mixture Model
- VAE的GMM解释
- 连续的GMM
- 求参数的函数如何确定
- 最大似然求解
- Conditional VAE
- Problems of VAE
- GAN(Generative Adversarial Network)
- The evolution of generation
- GAN-Discriminator的训练
- GAN-Generator的训练
- GAN-Toy Example
- In practical....…
- 参考文献
公式输入请参考: 在线Latex公式
接上节的内容,继续讲VAE。
Why VAE?
就是上节课中有一个非常突兀的公式,挖了个坑,这节课来填。先定性的看看他内部原理。
Intuitive Reason
先看下普通AE
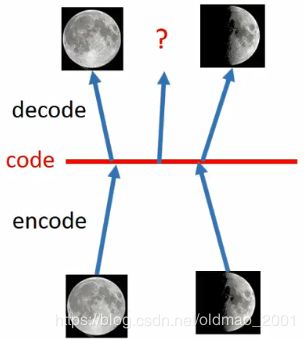
假设将满月的图片encoder后得到一个code,然后用decoder对code解码,得到满月的照片;
同样将半月的图片encoder后得到一个code,然后用decoder对code解码,得到半月的照片。
那如果要想得到介于满月和半月的照片是不是就直接从code的连线的中间取值后做decoder?
当然没有这么简单,因为code不会是这么简单线性关系,因此这样做效果是不确定的。
再看看VAE咋整的。
先贴VAE的模型:

可以看到每个encoder分了两个东西 σ \sigma σ和 m m m,每个东西三个值,所以相当于对code加上了噪声,相当于code有一定的范围,因此可以在这个范围内生成对应的图片。
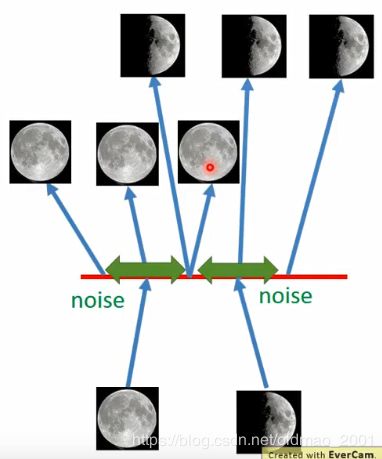
注意看中间部分,两个图片的code加上噪声之后中间有重叠部分,也就是说这个地方既要可以生成满月,又要生成半月图片,根据输入和输出之间的误差最小的目标,这个位置的图片只能是介于满月和半月之间了。
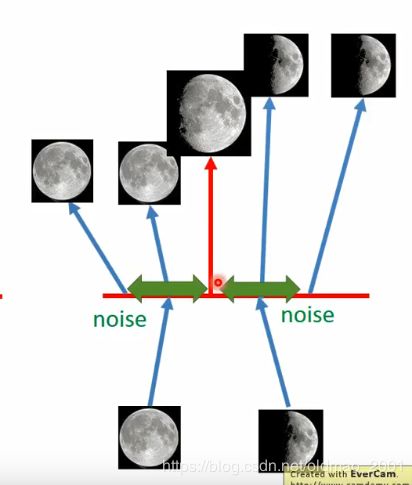
所以在VAE的模型中encoder生成的两个部分 σ \sigma σ和 m m m, m m m代表的是原始code,最后的 c c c是加上了噪声的code, σ \sigma σ代表原始code的variance,由于variance是正值,所以 σ \sigma σ做了指数操作,确保其为正数(那个公式: c i = e x p ( σ i ) × e i + m i c_i=exp(\sigma_i)\times e_i+m_i ci=exp(σi)×ei+mi),模型中的 e e e是从一个正态分布中sample出来的值。正态分布的variance是固定的,因此噪声的variance是由 σ \sigma σ决定的,因此variance是由模型自动学习到的。因此如果让机器自己来学习这个噪声variance是有点问题的(类似考试完让学生自己改卷,每个人都会改为100分),机器会直接让这个variance等于零,那么就相当于没有噪声,这个模型就和普通的AE是一样的了,没有什么区别。因此要对这个variance加以限制,不能让其太小,甚至等于零。
这个限制就是这个公式啦:
M i n i m i z e ∑ i = 1 3 ( e x p ( σ i ) − ( 1 + σ i ) + ( m i ) 2 ) Minimize\sum_{i=1}^3(exp(\sigma_i)-(1+\sigma_i)+(m_i)^2) Minimizei=1∑3(exp(σi)−(1+σi)+(mi)2)
这个公式里面 e x p ( σ i ) exp(\sigma_i) exp(σi)用蓝色表示, ( 1 + σ i ) (1+\sigma_i) (1+σi)用红色表示, e x p ( σ i ) − ( 1 + σ i ) exp(\sigma_i)-(1+\sigma_i) exp(σi)−(1+σi)用绿色表示,画出来:
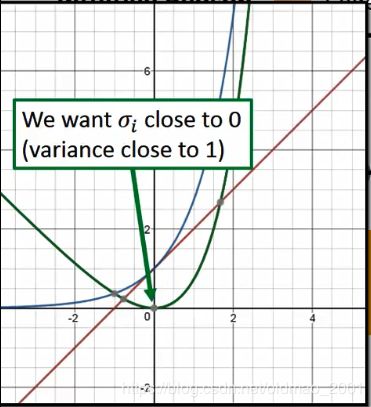
从绿色曲线可知,当 σ i \sigma_i σi接近0时,variance接近1。
最后的 ( m i ) 2 ) (m_i)^2) (mi)2)是L2正则化,让结果比较sparse。
以上是Intuitive Reason的说法,下面是论文中比较官方的说法。
这一段有点听得比较懵,因为涉及到了GMM,以及EM,这块比较弱的还是到B站去补一补
科学解释
先明确一下目标:

这里的 P ( x ) P(x) P(x)就是一个GMM,如果图形越接近宝可梦 P ( x ) P(x) P(x)就越大,图形乱七八糟 P ( x ) P(x) P(x)就越小。
要估计 P ( x ) P(x) P(x)就要用GMM
GMM Gaussian Mixture Model

P ( x ) = ∑ m P ( m ) P ( x ∣ m ) (1) P(x)=\sum_m P(m)P(x|m)\tag{1} P(x)=m∑P(m)P(x∣m)(1)
P ( m ) P(m) P(m)是组成混合高斯的每一个小高斯的权重,一共有m个高斯
如何从这m个简单高斯分布中sample 数据呢?
先要决定从哪一个高斯进行sample,也就是把这些个高斯分布看做一个multinomial的问题
于是这个决定的过程可以看做是一个关于m个样本的采样,从第m个高斯采样的概率是 P ( m ) P(m) P(m)。
找到指定的高斯了以后,再根据这个高斯的参数( μ m , Σ m \mu^m,\Sigma^m μm,Σm)进行采样:
x ∣ m ∼ N ( μ m , Σ m ) x|m\sim N(\mu^m,\Sigma^m) x∣m∼N(μm,Σm)
这里就很明白了,公式(1)中 P ( m ) P(m) P(m)是选择第m个高斯的概率,也可以看做权重; P ( x ∣ m ) P(x|m) P(x∣m)可以看做是从第m个高斯取数据x的概率。
现在如果我们手上有一系列的数据x(可以看到的,也叫观察变量),现在要估计m个高斯分布(看不到的,也叫隐变量)的各个参数( μ m , Σ m \mu^m,\Sigma^m μm,Σm),就是用EM算法。
从上面的讲解我们知道:
Each x you generate is from a mixture Distributed representation is better than cluster.
说人话:用某一个分类来表示是不够准确的,正确的做法是用一个分布来表示x,也就是说x可以表示为:有多少的几率从第a分布采样出来,有多少几率从b分布采样出来。。。。
理解这个,我们再回到VAE,VAE就可以看做是GMM中x的分布表示。
VAE的GMM解释
连续的GMM
实际上,上面的例子是组成GMM的m个高斯分布是不连续的,如果组成GMM的高斯是连续的呢?下面来描述一下这个情况
假设有一个变量z,这个z是从一个正态分布中采样出来的(z is a vector from normal distribution):
z ∼ N ( 0 , I ) z\sim N(0,I) z∼N(0,I)
z是一个向量,这个向量的每一个dimension带表观测变量的某一个属性(Each dimension of z represents an attribute)
如果我们先假设z是一维的,那么z的分布函数为:
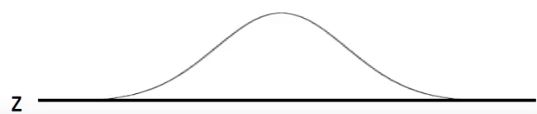
有了z之后,我们可以决定z对应的参数( μ , Σ \mu,\Sigma μ,Σ),这里和前面不一样了,这里的z是连续的分布,它和上面离散的GMM不一样了,刚才的GMM如果由10个高斯分布组成,那么对应的参数( μ , Σ \mu,\Sigma μ,Σ)也就有10组,是可以定下来的。这里的z表示连续的分布,也就意味着有无穷多个高斯分布,无穷多组参数( μ , Σ \mu,\Sigma μ,Σ),因此,这里我们用一个函数表示z所对应的高斯分布参数,写成:
μ ( z ) , σ ( z ) (2) \mu(z),\sigma(z)\tag{2} μ(z),σ(z)(2)
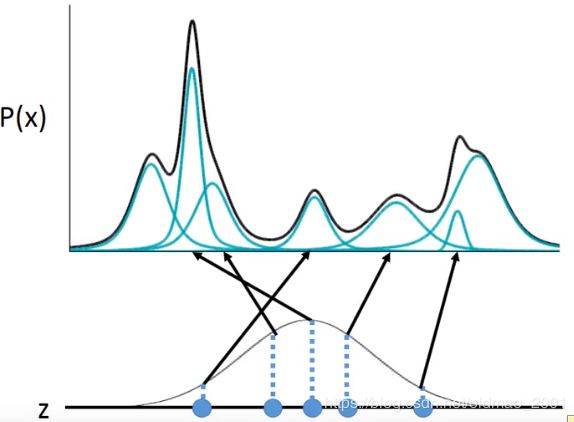
可以看到,我们从z从取了五个点,这五个点所对应高斯分布参数是由公式(2)决定的,从z的某一个高斯里面取出x的概率可以写成:
P ( x ∣ z ) ∼ N ( μ ( z ) , σ ( z ) ) P(x|z)\sim N(\mu(z),\sigma(z)) P(x∣z)∼N(μ(z),σ(z))
求参数的函数如何确定
现在面临的问题就是如何确定公式(2)中的函数是什么样子。

这里可以用一个NN来表示这个函数,也就是训练一个NN,输入一个z向量,输出是两个,分别是 μ ( z ) , σ ( z ) \mu(z),\sigma(z) μ(z),σ(z)
这个问题解决了之后,我们就可以写出来观测变量x的概率 P ( x ) P(x) P(x)
P ( x ) = ∫ z P ( z ) P ( x ∣ z ) d z (3) P(x)=\int_zP(z)P(x|z)dz\tag{3} P(x)=∫zP(z)P(x∣z)dz(3)
重要说明:上面的假设是z是从正态分布中采样出来的,实际上z的分布可以是非正态分布,无所谓是什么分布,因为中间从z估计参数的函数我们用的NN,NN号称啥函数都可以模拟,所以z的分布没有限制,因此最后得到的 P ( x ) P(x) P(x)也可以是很复杂形状。
最大似然求解
接下来要准备最麻烦的部分,去求隐变量z的参数,从上面的公式(3),以及已知条件,我们捋出下面信息:
P ( z ) P(z) P(z)是一个正态分布
P ( x ∣ z ) P(x|z) P(x∣z)是 N ( μ ( z ) , σ ( z ) ) N(\mu(z),\sigma(z)) N(μ(z),σ(z))分布
μ ( z ) , σ ( z ) \mu(z),\sigma(z) μ(z),σ(z)是我们要求的函数。
现在我们手上有一组观测变量x,希望找到一组函数 μ ( z ) , σ ( z ) \mu(z),\sigma(z) μ(z),σ(z)表达,使得x从 P ( x ) P(x) P(x)分布中取出来的概率最大。用最大似然的思想写出来的损失函数为:
L = ∑ x l o g P ( x ) (4) L=\sum_xlogP(x)\tag{4} L=x∑logP(x)(4)
这里是老师的分支讲解:
我们能调整的参数就是函数 μ ( z ) , σ ( z ) \mu(z),\sigma(z) μ(z),σ(z),而函数来自:

这里我们需要另外一个分布 q ( z ∣ x ) q(z|x) q(z∣x)
z ∣ x ∼ N ( μ ′ ( z ) , σ ′ ( z ) ) z|x\sim N(\mu'(z),\sigma'(z)) z∣x∼N(μ′(z),σ′(z))

这里,蓝色的NN就相当于VAE的Decoder,绿色的NN’相当于VAE的Encoder
根据公式(4):
l o g P ( x ) = ∫ z q ( z ∣ x ) l o g P ( x ) d z logP(x)=\int_zq(z|x)logP(x)dz logP(x)=∫zq(z∣x)logP(x)dz
由于 l o g P ( x ) logP(x) logP(x)和z无关,由于 ∫ z q ( z ∣ x ) d z = 1 \int_zq(z|x)dz=1 ∫zq(z∣x)dz=1(这里的 q ( z ∣ x ) q(z|x) q(z∣x)是任意一个分布,积分起来就是1),所以等式成立。
= ∫ z q ( z ∣ x ) l o g ( P ( z , x ) P ( z ∣ x ) ) d z =\int_zq(z|x)log\left(\frac{P(z,x)}{P(z|x)}\right)dz =∫zq(z∣x)log(P(z∣x)P(z,x))dz
这里为什么 P ( z , x ) P ( z ∣ x ) = P ( x ) \cfrac{P(z,x)}{P(z|x)}=P(x) P(z∣x)P(z,x)=P(x),分子是联合概率密度函数,这里是一个公式
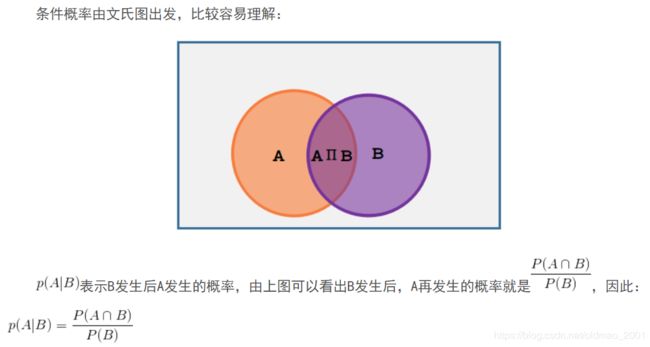
这里 P ( A ∩ B ) = P ( A , B ) P(A\cap B)=P(A,B) P(A∩B)=P(A,B)
ref:https://www.cnblogs.com/jiangkejie/p/10473427.html
= ∫ z q ( z ∣ x ) l o g ( P ( z , x ) q ( z ∣ x ) q ( z ∣ x ) P ( z ∣ x ) ) d z =\int_zq(z|x)log\left(\frac{P(z,x)}{q(z|x)}\frac{q(z|x)}{P(z|x)}\right)dz =∫zq(z∣x)log(q(z∣x)P(z,x)P(z∣x)q(z∣x))dz
log中乘可以变加法
= ∫ z q ( z ∣ x ) l o g ( P ( z , x ) q ( z ∣ x ) ) d z + ∫ z q ( z ∣ x ) l o g ( q ( z ∣ x ) P ( z ∣ x ) ) d z =\int_zq(z|x)log\left(\frac{P(z,x)}{q(z|x)}\right)dz+\int_zq(z|x)log\left(\frac{q(z|x)}{P(z|x)}\right)dz =∫zq(z∣x)log(q(z∣x)P(z,x))dz+∫zq(z∣x)log(P(z∣x)q(z∣x))dz
上式中的后面那项实际上是可以看成是两个分布的KL divergence,KL散度,写成:
K L ( q ( z ∣ x ) ∣ ∣ P ( z ∣ x ) ) ≥ 0 KL(q(z|x)||P(z|x))\geq0 KL(q(z∣x)∣∣P(z∣x))≥0
由于KL是衡量两个分布是否相似的概念,相当于两个分布的距离,KL越小距离越小,分布越像,因此这个距离是不可能小于0的。因此我们可以得到如下不等式:
L = ∑ x l o g P ( x ) ≥ ∫ z q ( z ∣ x ) l o g ( P ( z , x ) q ( z ∣ x ) ) d z L=\sum_xlogP(x)\geq \int_zq(z|x)log\left(\frac{P(z,x)}{q(z|x)}\right)dz L=x∑logP(x)≥∫zq(z∣x)log(q(z∣x)P(z,x))dz
由于 P ( z , x ) = P ( x ∣ z ) P ( z ) P(z,x)=P(x|z)P(z) P(z,x)=P(x∣z)P(z),有:
L = ∑ x l o g P ( x ) ≥ ∫ z q ( z ∣ x ) l o g ( P ( x ∣ z ) P ( z ) q ( z ∣ x ) ) d z L=\sum_xlogP(x)\geq \int_zq(z|x)log\left(\frac{P(x|z)P(z)}{q(z|x)}\right)dz L=x∑logP(x)≥∫zq(z∣x)log(q(z∣x)P(x∣z)P(z))dz
不等式的右边就是L的下限,英文名字叫lower bound,简称: L b L_b Lb,故有:
l o g P ( x ) = L b + K L ( q ( z ∣ x ) ∣ ∣ P ( z ∣ x ) ) logP(x)=L_b+KL(q(z|x)||P(z|x)) logP(x)=Lb+KL(q(z∣x)∣∣P(z∣x))
要使得 l o g P ( x ) = logP(x)= logP(x)=最大,那么就是要让 L b L_b Lb最大,即:
L b = ∫ z q ( z ∣ x ) l o g ( P ( x ∣ z ) P ( z ) q ( z ∣ x ) ) d z L_b=\int_zq(z|x)log\left(\frac{P(x|z)P(z)}{q(z|x)}\right)dz Lb=∫zq(z∣x)log(q(z∣x)P(x∣z)P(z))dz
这里就是要找到: P ( x ∣ z ) P(x|z) P(x∣z)和 q ( z ∣ x ) q(z|x) q(z∣x)使得 L b L_b Lb最大
划重点:虽然提到 L b L_b Lb有助于提高likelihood,但只能提高likelihood的最小值,我们并不知道likelihood和 L b L_b Lb之间的距离是多少,也就是说当我们提高 L b L_b Lb的时候likelihood是有可能下降的。
我们来看图:

当我们固定 P ( x ∣ z ) P(x|z) P(x∣z)这项,最大化 q ( z ∣ x ) q(z|x) q(z∣x),会发现, l o g P ( x ) logP(x) logP(x)不变,KL在减少, L b L_b Lb越来越接近likelihood,即 l o g P ( x ) logP(x) logP(x),当 q ( z ∣ x ) = P ( x ∣ z ) q(z|x)=P(x|z) q(z∣x)=P(x∣z),两个分布一样,KL为0, L b = l o g P ( x ) L_b=logP(x) Lb=logP(x),这个时候如果再提高 L b L_b Lb,就会使得 l o g P ( x ) logP(x) logP(x)变大。也就是说,最后两个分布 q ( z ∣ x ) q(z|x) q(z∣x)和 P ( x ∣ z ) P(x|z) P(x∣z)会趋向于一致。
下面来研究一下 L b L_b Lb
L b = ∫ z q ( z ∣ x ) l o g ( P ( x ∣ z ) P ( z ) q ( z ∣ x ) ) d z = ∫ z q ( z ∣ x ) l o g ( P ( z ) q ( z ∣ x ) ) d z + ∫ z q ( z ∣ x ) l o g P ( x ∣ z ) d z L_b=\int_zq(z|x)log\left(\frac{P(x|z)P(z)}{q(z|x)}\right)dz\\ =\int_zq(z|x)log\left(\frac{P(z)}{q(z|x)}\right)dz+\int_zq(z|x)logP(x|z)dz Lb=∫zq(z∣x)log(q(z∣x)P(x∣z)P(z))dz=∫zq(z∣x)log(q(z∣x)P(z))dz+∫zq(z∣x)logP(x∣z)dz
看下上面的左边这项,刚好是 − K L ( q ( z ∣ x ) ∣ ∣ P ( z ) ) -KL(q(z|x)||P(z)) −KL(q(z∣x)∣∣P(z))
这里注意:
q ( z ∣ x ) q(z|x) q(z∣x)是之前说的NN’,即给定x,可以得到z的分布(求出参数就是得到分布)

由于有负号的存在,所以就变成了
M i n i m i z i n g K L ( q ( z ∣ x ) ∣ ∣ P ( z ) ) Minimizing\quad KL(q(z|x)||P(z)) MinimizingKL(q(z∣x)∣∣P(z))
让一个KL散度最小,就是要使得两个分布越接近越好,也就是要是NN’生成的分布要和 P ( z ) P(z) P(z)越接近越好。
根据VAE论文的附录B,可以推导到最后就是下面这个条件:
m i n i m i z e ∑ i = 1 3 ( e x p ( σ i ) − ( 1 + σ i ) + ( m i ) 2 ) minimize\quad \sum_{i=1}^3(exp(\sigma_i)-(1+\sigma_i)+(m_i)^2) minimizei=1∑3(exp(σi)−(1+σi)+(mi)2)
再看 L b L_b Lb式子的右边一项,要最大化这项:
∫ z q ( z ∣ x ) l o g P ( x ∣ z ) d z \int_zq(z|x)logP(x|z)dz ∫zq(z∣x)logP(x∣z)dz
可以把 q ( z ∣ x ) q(z|x) q(z∣x)看成weighted sum,上式可以写成:
= E q ( z ∣ x ) [ l o g P ( x ∣ z ) ] =E_{q(z|x)}[logP(x|z)] =Eq(z∣x)[logP(x∣z)]
E q ( z ∣ x ) E_{q(z|x)} Eq(z∣x)就是期望。相当于下图的红线部分,后面的相当与黄线部分

通俗的说,就是要用给定的x找到一个分布z(这个分布当然是通过参数 μ ′ ( z ) , σ ′ ( z ) \mu'(z),\sigma'(z) μ′(z),σ′(z)来确定的,这个分布可以通过NN找到一个分布,使得 P ( x ) P(x) P(x)最大)。
当我们不考虑方差 σ \sigma σ(实作是这样搞的),只考虑均值 μ \mu μ,我们会想让 μ ( x ) \mu(x) μ(x)越接近x越好,在高斯分布中,均值就是最接近x的,这个时候的 l o g P ( x ∣ z ) logP(x|z) logP(x∣z)最大。上面的模型就是一个VAE,如下图:

到这里算是完结了。。。
Conditional VAE
先将手写的数字丢到decoder,得到这个数字的特征,然后在Encoder的过程中加入其它数字的限制,就会用之前学习到的数字特征生成其它数字的图片,如下图所示,第一列是原始数字,后面是Conditional VAE生成的数字。

上面是MINST数据集做的结果,下面是另外一个数据集。
下面是参考文献:
· Carl Doersch, Tutorial on Variational Autoencoders
· Diederik P. Kingma, Danilo J. Rezende, Shakir Mohamed, Max Welling,"Semi-supervised learning with deep generative models."NIPS,2014.
· Sohn, Kihyuk, Honglak Lee, and Xinchen Yan,"Learning Structured Output Representation using Deep Conditional Generative Models."N/PS,2015.
· Xinchen Yan, Jimei Yang, Kihyuk Sohn, Honglak Lee, “Attribute2lmage: Conditional Image Generation from Visual Attributes”, ECCV,2016
· Cool demo:
· https://vdumoulin.github.io/morphing_faces/(这个是用VAE来生成不同的脸的程序)
· http://fvae.ail.tokyo/(访问失败了)
Problems of VAE
问题在于没有真的在想要生成一个真实的图片,只是生成一个图片就完事。例如:
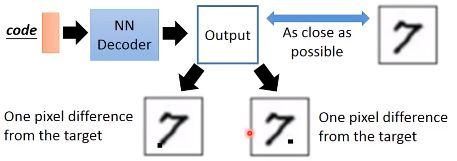
这里,VAE生成的图片和原图都只有一个像素不一致,从相似度计算来说两个结果都一样的,VAE可能认为右边的就ok了,这样是不好的。从本质上讲,VAE只不过是把原来的图片进行了一个linear combination的修改,没有去生成一个新的图片。
因此为了解决这个问题,就提出了GAN
GAN(Generative Adversarial Network)
lan J. Good fellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio, Generative Adversarial Networks, arXiv preprint 2014.
http://peellden.pixnet.net/blog/post/40406899-2013-%E7%AC%AC%E5%9B%9B%E5%AD%A3%EF%BC9%8C%E5%86%AC%E8%9D%B6%E5%AF%82%E5%AF%A5
The evolution of generation

这里的Generator没有看过real image,所以它产生的图片是和原有的real image完全不一样的。
GAN-Discriminator的训练
先用Generator生成一些图片,Generator和VAE的decoder结构差不多,输入不同的向量,得到的图片也就不一样,然后和真实图片放在一起。
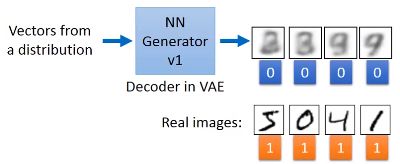
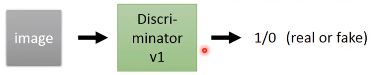
然后输入到Discriminator中,做一个二分类的训练,让其分辨出假图片(0)和真图片(1)
GAN-Generator的训练
刚开始,随机生成一个向量,并输入到Generator中,然后Generator生成一个图片,Discriminator会给出这个图片是真实图片的概率,例如:0.87
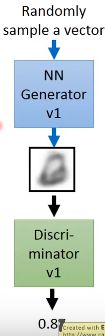
然后调节(tuning)Generator的参数,使得Generator的输入在Discriminator的判断越接近1越好。
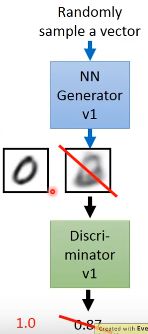
调整方式:
把两个都看成一个大的NN:Generator +Discriminator=a network
然后使用梯度下降更新Generator的参数。 Using gradient descent to find the parameters of generator。
需要注意的是,调节Generator的参数的同时,要把Discriminator的参数固定住。
GAN-Toy Example
Demo:http://cs.stanford.edu/people/karpathy/gan/
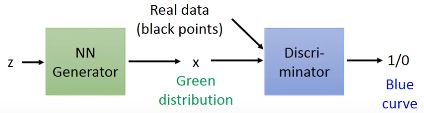
这里的z是一个均匀分布,绿色和蓝色是Generator和Discriminator生成的分布,黑色是实际数据。

上面是训练的过程,注意绿色的分布逐渐向黑色分布靠拢,当然如果参数设置不好,会靠过头,偏向左边。注意看下面的z到x的箭头指向。
例子:CIFAR10的数据集

ref:https://openai.com/blog/generative-models/
In practical……
·GANs are difficult to optimize.
·No explicit signal about how good the generator is
·In standard NNs,we monitor loss
·In GANs,we have to keep"well-matched in a contest"
·When discriminator fails,it does not guarantee that generator generates realistic images.
·Just because discriminator is stupid
·Sometimes generator find a specific example that can fail the discriminator(罩门学说)
·Making discriminator more robust may be helpful.
参考文献
·“Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks”
·“Improved Techniques for Training GANs”
·“Autoencoding beyond pixels using a learned similarity metric”
·“Deep Generative Image Models using a Laplacian Pyramid of Adversarial Network”
·“Super Resolution using GANs”