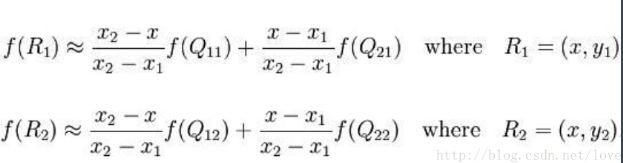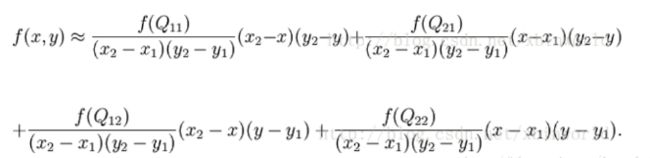【图像处理基础】1.图像插值算法

---

1.图像插值算法原理介绍

所谓插值算法，意思是在已有图片的情况下，在像素与像素之间插入新的像素，当然不止是用于像素插入使图像扩增，也可以用于图像缩放，那么新的像素怎么取值呢，下面介绍两种取值方法。

1.1最近邻插值算法

顾名思义，最近邻插值算法值的是插的新像素与和它最相邻像素的取值相同。

如上图所示，若插入的新像素位于P位置，可以看到Q11与它最近，所以f( P)=f(Q11)。

• 算法过程：
  最近邻插值算法的过程是首先假设原图是一个像素大小为W×H的图片，缩放后的图片是一个像素大小为w×h的图片，这时候我们是已知原图中每个像素点上的像素值（即灰度值等）的（⚠️像素点对应像素值的坐标都是整数）。这个时候已知缩放后有一个像素点为(X,Y)，想要得到该像素点的像素值，那么就要根据缩放比例去查看其对应的原图的像素点的像素值(x,y)，然后将该像素值赋值给该缩放后图片的像素点(X,Y)

• 缩放公式：
  根据横轴，即宽可得：X/x = W/w
  根据纵轴，即高可得：Y/y = H/h
  那么能够得到 f（X,Y）= f( W/w × x, H/h ×y)
  因此这个时候缩放后的图片像素点(x,y)的像素值就对应着原图像素点( W/w × x, H/h ×y)的像素值，若这个值非整数，则根据最近邻插值法，四舍五入取离这个值最近的整数作为最终结果。

• 举例说明：

  • 放大图片的例子
    若将1副3×3的图片放大的4×4，用f(x,y)表示目标图像，h(x,y)表示原图像。
    则f（x,y）=h(3/4×x,3/4×y)
    所以f(1,1)=h(0.75,0.75)=h(1,1),f(0,3)=h(0,2.25)=h(0,2)

  • 缩小图片的例子
    若将1副5×5的图片缩小成3×3
    则 f(x,y)=h(5/3×x，5/3×y)
    所以，f(1,1)=h(5/3,5/3)=h(2,2), f(0,3)=h(0,5)

• 优缺点
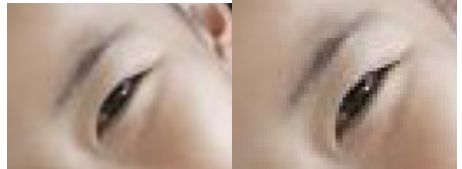
  这种方法的好处就是简单，但是坏处就是太过粗暴，会缺失精度，造成缩放后的图像灰度上的不连续，在变化地方可能出现明显块状效应，如下图所示：
  

1.2线性插值法

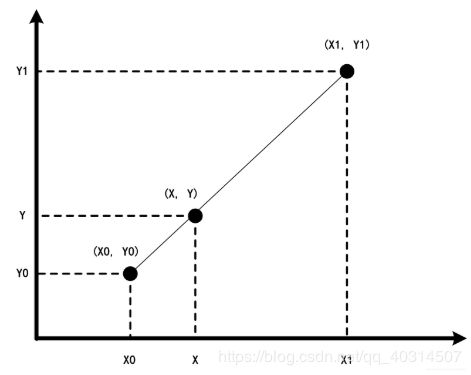
如图所示，我们已知(x0,y0),(x1,y1)和x，需要求得y的值
可以得到：

进而得到：

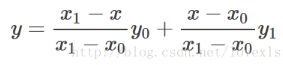
可以看到，y的值的求法是用x和x0，x1的距离作为一个权重，用于y0和y1的加权。

1.3双线性插值

双线性插值是线性插值在二维时的推广，其核心思想是在两个方向分别进行一次线性插值。

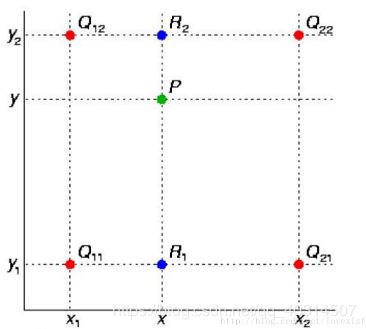
假如我们想得到未知函数 f 在点 P = (x, y) 的值，假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。最常见的情况，f就是一个像素点的像素值。

1. 首先在 x 方向进行线性插值，得到
   
2. 然后在y方向进行线性插值，得到
   

综合起来就是双线性插值最后的结果：

2.映射与插值

2.1向前映射

向前映射方法是，以原图每个像素为基准计算被它影响的新图像素。
参考博客:https://blog.csdn.net/glorydream2015/article/details/44873703
下图为向前映射示意图，输入图像上整数点坐标映射到输出图像之后，变成了非整数点坐标。因此，需要将其像素值按一定权重分配到其周围四个像素点上。对于输出图像而言，其整数点像素值周围会有很多输入图像像素映射过来，每个到其周围的非整数点像素值都会分配一定的灰度值到它上面，将这些分配而来的像素值叠加，就是输出图像整数点位置的像素值。由于这个分配、叠加的特性，向前映射法有时也叫像素移交映射。

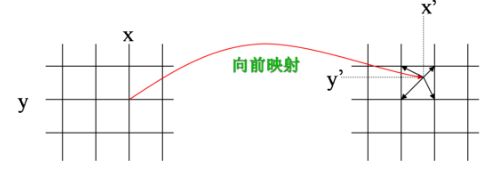
因此，对于向前映射而言，输出图像某一点的像素值不能直接得到，需要遍历输入图像的所有像素值，对其进行坐标变换，分配像素值到整数位置，才能得到输出图像各像素点的像素值。这是向前映射法的缺点。

2.2向后映射

向后映射的方法是，以新图每个像素为基准计算影响它的原图像素。
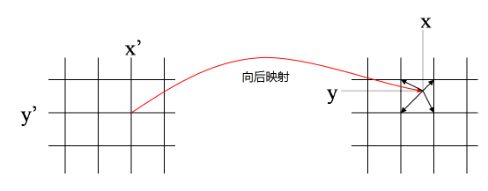
向后映射法就比较直观。在这种情况下，我们知道输出图像上整数点位置(x’,y’)在变换前位于输入图像上的位置(x,y)，一般来说这是个非整数点位置，利用其周围整数点位置的输入图像像素值进行插值，就得到了该点的像素值。我们遍历输出图像，经过坐标变换、插值两步操作，我们就能将其像素值一个个地计算出来，因此向后映射又叫图像填充映射。如下图所示。

2.3总结

• 向前映射，是以原图每个像素为基准计算被它影响的新图像素，若一个输入像素被映射到四个输出像素之间的位置，则其灰度值要按插值算法在4个输出像素之间进行分配，因为每个输出像素的整数像素值可能受到很多在从输入像素映射到四个输出像素之间的位置的点的影响，所以输出像素的整数像素值的确定需要遍历所有输入像素之后才能确定。
• 而向后映射将输出像素映射到输入像素后，若是被映射到四个输入像素之间的位置，只需要插值之后就得到了该点的像素值，只需要求该点的像素值，不需要考虑再分配问题。

3.python插值函数

cv2.resize函数，可以用插值算法实现图片缩放。

• 函数原型

cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]])

• 参数：

参数	描述
src	【必需】原图像
dsize	【必需】输出图像所需大小
fx	【可选】沿垂直轴的比例因子
interpolation	【可选】插值方式

• 插值方式：

cv.INTER_NEAREST	最近邻插值
cv.INTER_LINEAR	双线性插值
cv.INTER_CUBIC	基于4x4像素邻域的3次插值法
cv.INTER_AREA	基于局部像素的重采样

示例代码如下：

import cv2
import matplotlib.pyplot as plt
from PIL import Image
import os

%matplotlib inline
if __name__ == "__main__":
    img = cv2.imread('F:/study/cv_base/girl.jpg')
    img = img[:, :, [2, 1, 0]]#转换成RGB,因为cv2读的是BGR，而plt需要RGB
    plt.imshow(img)
    print('Original Dimensions : ',img.shape)
    
    scale_percent = 30       # percent of original size
    width = int(img.shape[1] * scale_percent / 100)
    height = int(img.shape[0] * scale_percent / 100)
    dim = (width, height)
    # resize image
    resized = cv2.resize(img, dim, interpolation = cv2.INTER_LINEAR)
    fx = 1.5
    fy = 1.5
    resized1 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation = cv2.INTER_NEAREST)
    resized2 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation = cv2.INTER_LINEAR)
    print('Resized Dimensions : ',resized.shape)

结果：

然后把插值后的打印出来：

plt.figure("Resized image") # 图像窗口名称
plt.title('Resized image') # 图像题目
plt.imshow(resized)
plt.figure("INTER_NEAREST image") # 图像窗口名称
plt.title("INTER_NEAREST image") # 图像窗口名称
plt.imshow(resized1)
plt.figure("INTER_LINEAR image") # 图像窗口名称
plt.title("INTER_LINEAR image") # 图像窗口名称
plt.imshow(resized2)

0.3倍缩放：

将缩放后的1.5倍放大，最邻近插值：

将缩放后的1.5倍放大，双线性插值：