字符串匹配 —— KMP 算法
它的代码很短很短~神奇的是我每次使用都会把原理忘掉~
KMP 算法最普遍的用途很简单,就是给出字符串 A 和字符串 B,其中 B 的长度小于 A 。问 B 是否为 A 的子串 ? 而 KMP 算法则用于快速地回答这个问题。
KMP 算法的匹配过程是这样的:
此时 A 串的 b 与 B 串的 c 失配;传统的暴力匹配就是在失配的时候把模式串(B 串)整个右移一位然后重新匹配。然而右移一位开始匹配必然会一开始就失配;因为我们根据前面的匹配过程已经知道 A[1] = b 且 B[0] = a;在这里右移一位开始匹配是没有意义的。
所以有没有办法让 A 串的 b 与 B 串的 c 失配时,能让模式串右移尽可能多的位数而不影响结果呢?有的。失配的时候可以得到的信息是:B 串 c 之前的字符串都成功地与 A 串匹配;这时要有最长公共前后缀(Longest common prefixes and suffixes)的概念:公共前后缀就是字符串的前缀和后缀是相同的子串,而最长的那一对就是最长公共前后缀(简称:LCPS)。
比如字符串 cacac
前缀有(从前面数起):c、ca、cac、caca
后缀有(从后面数起):c、ac、cac、acac
可以看到 c、cac 都是字符串 cacac 的公共前后缀,且 cac 是 LCPS。
所以 B 串失配点 c 之前的字符串 ababa 的 LCPS 是 aba (也即是 A 串失配点 b 之前的字符串 ababa 的后缀)。而 B 串需要右移到 B 串失配点前的字符串的前缀(且以 LCPS 为前缀)和 A 串失配点前的字符串的后缀重合的地方(仔细观察可以发现其实就是移动到 B[strlen(LCPS)] 与 A[5](A 串失配点)重合的地方),然后变成这样:
然后从失配点 A[5] 开始匹配(因为前面的都一样是 aba)。按照一样的方法依次可得:
所以问题在于求出模式串(B 串)所有前缀的 LCPS (其实仅仅需要的是 LCPS 的长度),我们用一个数组 next[] 来表示。next[i] = k 表示模式串下标为 0 ~ i-1 的子串的 LCPS 长度为 k。则 ababacb 的 next 数组如下:
下标: 0 1 2 3 4 5 6
next:-1 0 0 1 2 3 0
匹配过程的伪代码:
KMP_Searsh(string, pattern)
begin
i = 0;
j = 0;
slen = strlen(string);
plen = strlen(pattern);
while i < slen && j < plen
if j == -1 or string[i] == pattarn[j]
i++;
j++;
else
j = next[j];
end
end
if j == plen
return i - j; //匹配成功,返回 pattern 在 string 的起始下标
else
return -1;
end根据伪代码仔细想想就能明白为什么 next[0] = -1。
所以剩下的问题是 next 数组怎样求?我们先用归纳法的思想去理解这个过程:
假设我们知道了 next[j] = k,怎样求 next[j+1] ?
举个鲜活的例子,设模式串 P 为:
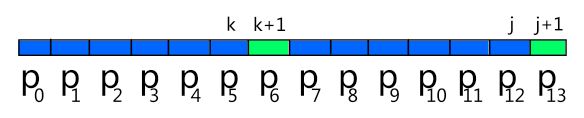
假如 j = 12, k = 5;则有 next[12] = 5。
也就是说子串 P0~P11 的 LCPS 的长度为 5,也即子串 P0~P4 和子串 P7~P11 是相同的;这是我们假设已经知道了的;接着我们看怎样求 next[13]。
影响 next[j+1] (即next[13])结果的只有两种情况:
1)k == j
2)k != j
第一种就好办了,直接 next[j+1] = next[j] + 1 = k + 1;即是 next[13] = 6;如下:
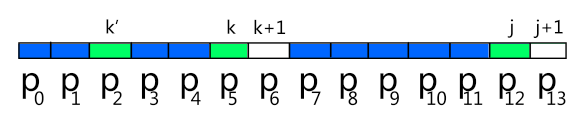
第二种就不太好理解了,由于 k != j,则子串 P0~P12 就不可能有长度为 k + 1 = 6 的 LCPS(即 next[j+1] < 6)。那我们可以找更短的 LCPS;可能的情况为:
长度为 1:P0 和 P12
长度为 2:P0~P1 和 P11~P12
长度为 3:P0~P2 和 P10~P12
长度为 4:P0~P3 和 P9~P12
长度为 5:P0~P4 和 P8~P12
那要逐个去试?不。这里我们增加一些东西,既然我们假设 next[j] = k,那一定有 k < j,而且 j 之前的 next 值肯定是已经计算了的,所以为了下面的理解,我们再设 next[k] = k',令 k' = 2,则 next[5] = 2。
这时我们求 next[j+1] 就要这样了:如果 P[next[k]] == P[j],则 P[j+1] = next[k] + 1;否则继续判断如果有 P[next[next[k]]] == P[j],则 P[j+1] = next[next[k]] + 1,... ;如果遇到 next[0] = -1,则 P[j+1] = 0。
为什么这样?首先,因为 next[k] = k',那子串 P0~P1 和子串 P3~P4 是相同的;而 next[j] = k 可知子串 P0~P4 和子串 P7~P11 是相同的,当然子串 P3~P4 和子串 P10~P11 也是相同的;从而知道子串 P0~P1 和子串 P10~P11 也是相同的。所以如果 P[next[k]] == P[j](即P[k'] == P[j]),那子串 P0~P2 和子串 P10~P12 就是相同的!也即是 P[j+1] = next[k] + 1(即 next[13] = 3);如下:
我们知道 next[13] < 6,根据上面过程也知道子串 P0~P12 有长度为 3 的公共前后缀;但何以得知 next[13] 的 LCPS 就是 3,而不是 4 或 5?
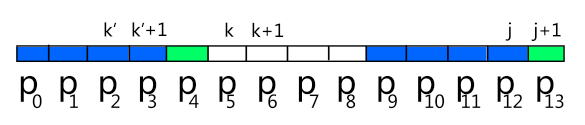
来,反证法。回到最初的起点,有 next[12] = 5;next[5] = 2;如果 next[13] = 4,则有:
这表示子串 P0~P3 和子串 P9~P12 是相同的,作为子串的子串,子串 P0~P2 和 子串 P9~P11 当然也是相同的;而由 next[12] = 5 知,子串 P0~P4 和子串 P7~P11 是相同的,作为子串的子串,子串 P2~P4 和 子串 P9~P11 当然也是相同的;这会有什么问题?这代表子串 P0~P2 和子串 P2~P4 是相同的!而这导致的结果是 next[5] = 3;这就出问题了,因为我们假设的是 next[5] = 2;产生了矛盾。令 next[13] = 5 也会得到类似的现象;所以 next[13] = 3 是正确的!当然,子串 P0~P12 可能有长度比 3 小的公共前后缀,但我们并不需要那些信息。
而如果 P[next[k]] != P[j],按照上面的过程类似做下去即可求出 next[j+1]。且第二种情况求出的结果必有 next[j+1] < next[j]。
伪代码为:
getNextVal(pattern)
begin
k = -1;
j = 0;
next[j] = k;
len = strlen(pattern);
while j < len
if k == -1 || pattern[j] == pattern[k]
k++;
j++;
next[j] = k;
else
k = next[k];
end
end
end以上就是 KMP 算法的最基本的内容,然而上面的方法存在一个效率上的小问题,看这样一个情况:
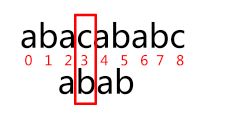
字符串 abab 的 next 数组为:-1, 0, 0, 1。失配后右移为:
匹配再次失败,其实这个移动也是不必要的;因为由第一次匹配知 s[3] != p[3](s 为匹配串,p 为模式串),而第二次匹配起点 p[next[3]] == p[1] == p[3] == 'b',所以 p[1] != s[3] 是必然的。会出现这种情况是因为 next 数组中出现了 p[next[j]] == p[j]。 要避免这种情况的话,我们需要在 p[j] == p[next[j]] 的时候再次递归,令 next[j] = next[next[j]]。
修改后伪代码为:
getNextVal(pattern)
begin
k = -1;
j = 0;
next[j] = k;
len = strlen(pattern);
while j < len
if k == -1 || pattern[j] == pattern[k]
k++;
j++;
if(pattern[j] == pattern[k])
next[j] = next[k]; //这里写成迭代的形式,手动模拟一下 abab 那个例子会比较好理解
else
next[j] = k;
end
else
k = next[k];
end
end
end接着看一下 KMP 算法的时间复杂度:
我们发现如果某个字符匹配成功,模式串首字符的位置保持不动,仅仅是 i++、j++;如果匹配失配,i 不变(即 i 不回溯),模式串会跳过匹配过的 next[j] 个字符。整个算法最坏的情况是,当模式串首字符位于 i - j 的位置时才匹配成功,算法结束。所以,如果文本串的长度为 n,模式串的长度为 m,那么匹配过程的时间复杂度为 O(n),算上计算
next 的 O(m) 时间,KMP的整体时间复杂度为 O(m + n)。
最后用 C 语言解决这个例子:
#include
#include
int next[100];
void getNextVal(char *pattern){
int k = -1;
int j = 0;
int len = strlen(pattern);
next[j] = k;
while(j < len){
if(k == -1 || pattern[j] == pattern[k]){
k++;
j++;
if(pattern[j] == pattern[k])
next[j] = next[k];
else
next[j] = k;
}
else
k = next[k];
}
}
int KMP_Searsh(char *str, char *pattern){
int i = 0;
int j = 0;
int slen = strlen(str);
int plen = strlen(pattern);
while(i < slen && j < plen){
if(j == -1 || str[i] == pattern[j]){
i++;
j++;
}
else
j = next[j];
}
if(j == plen)
return i - j;
return -1;
}
int main()
{
int i;
int ans;
char str[] = {"abababaababacb"};
char pattern[] = {"ababacb"};
getNextVal(pattern);
ans = KMP_Searsh(str, pattern);
for(i = 0; i < strlen(pattern); i++)
printf("%d ", next[i]);
printf("\n");
if(ans != -1)
printf("match! begin subscript: %d\n", ans);
else
printf("not match!\n");
return 0;
}
练习:
POJ 3461 —— Oulipo
POJ 1961 —— Period
KMP 算法还有其他扩展,日后有时间或者用到的话就补上~
本文参考资料:http://blog.csdn.net/v_july_v/article/details/7041827