python学习-综合练习七（二分查找（递归）、线性查找、插入排序、快速排序、选择排序、冒泡排序、归并排序、堆排序）-实例
文章目录
- 二分查找
- 线性查找
- 插入排序
- 快速排序
- 选择排序
- 冒泡排序
- 归并排序
- 堆排序
- 推荐代码一
- 推荐代码二
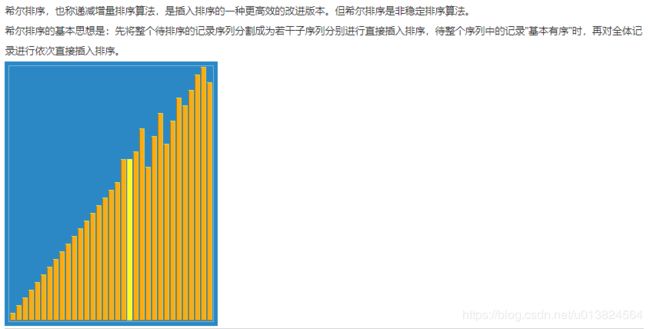
- 希尔排序
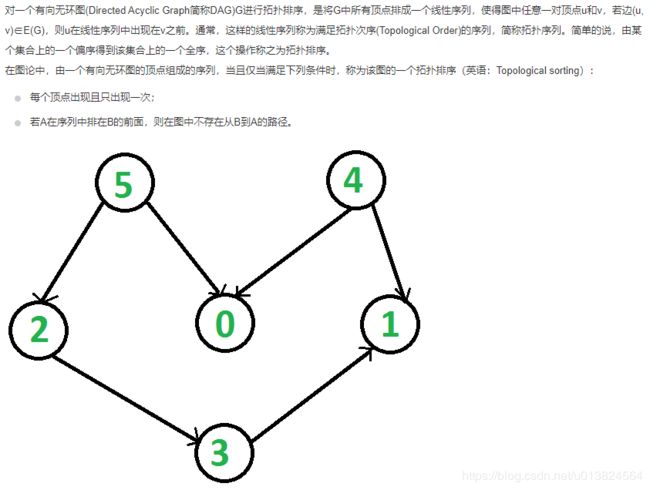
- 拓扑排序
说明：本篇博文的知识点大部分来自 Python3 实例
二分查找
二分搜索是一种在有序数组中查找某一特定元素的搜索算法。
这种搜索算法每一次比较都使搜索范围缩小一半。
二分查找有一个特定条件，对于有序且从小到大排列的容器才能使用
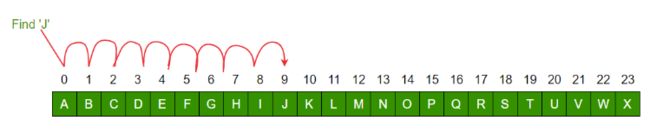
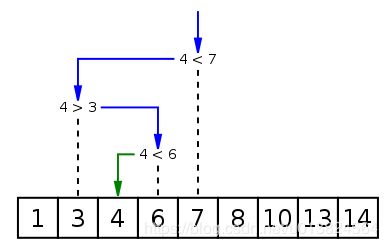
这是从菜鸟教程里面截取的一张图，很好的解释了二分查找。
输入数值为4，一半是第五位：7，小于7，在前半部分。再一半取得第二位：3，大于3，在3之后的半部分里面，这样一直二分，直到查找到最终结果。
def binarySearch(lst2, fst, len1, num1):
if len1 >= fst:
mid = int(fst + (len1 - fst) / 2)
if lst2[mid] == num1:
return mid
elif lst2[mid] > num1:
return binarySearch(lst2, fst, mid - 1, num1)
else:
return binarySearch(lst2, mid + 1, len1, num1)
else:
return -1
lst1 = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
rst = binarySearch(lst1, 0, len(lst1) - 1, 8)
if rst != -1:
print("元素在列表中的索引为 ", rst)
else:
print("元素不在数组中")
运行结果：
线性查找
线性查找指按一定的顺序检查数组中每一个元素，直到找到所要寻找的特定值为止。
这是从菜鸟教程里面截取的一张图，很好的解释了二分查找。
我个人觉得这个就是常用的变量，没什么特别的。
上代码：
lst2 = [2, 3, 4, 5, 6, 7, 8, 9]
def search(lst3, len3, num3):
for idx in range(0, len3):
if lst3[idx] == num3:
return idx
return -1
num2 = 6
rst2 = search(lst2, len(lst2), num2)
if rst2 != -1:
print("元素在数组中的索引为", rst2)
else:
print("元素不在数组中")
运行结果：
插入排序
插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
Python 插入排序
插入排序大家进入这个网址取看吧。主要他的那个动图很有形象。弄不过来。
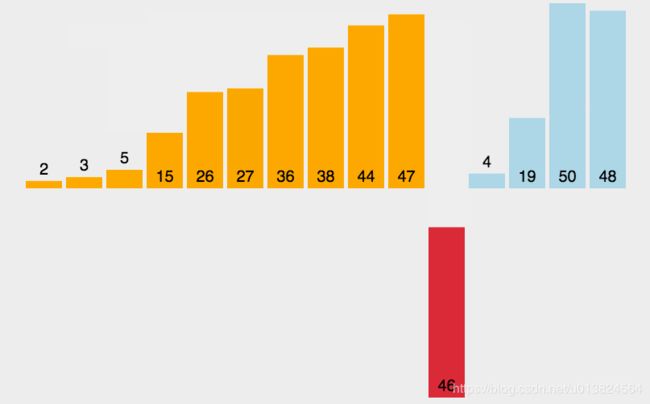
这张图，可以去网址里面看看它的实现逻辑。Python 插入排序
上代码：
def insertionSort(lst5):
for idx1 in range(1, len(lst5)):
key = lst5[idx1]
idx2 = idx1 - 1
while idx2 >= 0 and key < lst5[idx2]:
lst5[idx2 + 1] = lst5[idx2]
idx2 -= 1
lst5[idx2 + 1] = key
lst4 = [12, 11, 13, 5, 6, 234, 1]
insertionSort(lst4)
print("排序后的数组:")
for i in range(len(lst4)):
print("%d" % lst4[i])
运行结果：
快速排序
快速排序使用分治法策略来把一个序列分为较小和较大的2个子序列，然后递归地排序两个子序列。
def partition(lst03, low, high):
idx1 = (low - 1)
pivot = lst03[high]
for j in range(low, high):
if lst03[j] <= pivot:
idx1 = idx1 + 1
lst03[idx1], lst03[j] = lst03[j], lst03[idx1]
lst03[idx1 + 1], lst03[high] = lst03[high], lst03[idx1 + 1]
return idx1 + 1
def quickSort(lst02, low, high):
if low < high:
pi = partition(lst02, low, high)
quickSort(lst02, low, pi - 1)
quickSort(lst02, pi + 1, high)
lst01 = [10, 7, 8, 9, 1, 5]
quickSort(lst01, 0, len(lst01) - 1)
print("排序后的数组:")
for i in range(len(lst01)):
print("lst01[{idx}] = {val}".format(idx=i, val=lst01[i]))
运行结果：
选择排序
选择排序是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
这也是从菜鸟教程里面截取的一张图：
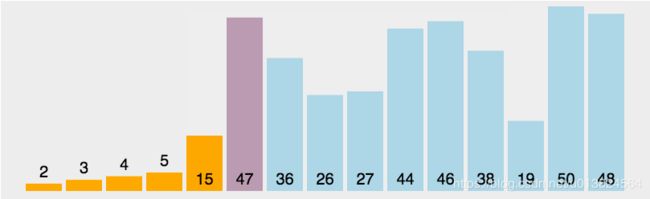
这张图，可以去网址里面看看它的实现逻辑。Python 选择排序
lst03 = [64, 25, 12, 22, 11, 35, 2, 9, 123]
for i in range(len(lst03)):
minIdx = i
for j in range(i + 1, len(lst03)):
if lst03[minIdx] > lst03[j]:
minIdx = j
lst03[i], lst03[minIdx] = lst03[minIdx], lst03[i]
print("排序后的数组：")
for i in range(len(lst03)):
print("lst03[{idx}] = {val}".format(idx=i, val=lst03[i]))
运行结果：
冒泡排序
冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。
走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。
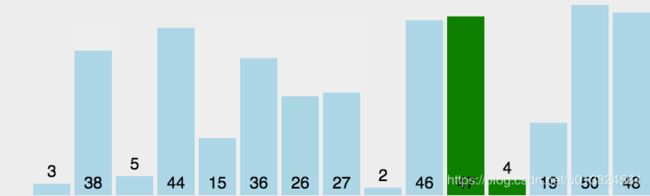
这张图，可以去网址里面看看它的实现逻辑。Python 冒泡排序
代码：
lst04 = [23, 64, 25, 11, 76, 12, 22]
def bubbleSort(lst05):
n = len(lst05)
for idx1 in range(n):
for idx2 in range(0, n - idx1 - 1):
if lst05[idx2] > lst05[idx2 + 1]:
lst05[idx2], lst05[idx2 + 1] = lst05[idx2 + 1], lst05[idx2]
bubbleSort(lst04)
print("排序后的数组:")
for i in range(len(lst04)):
print("lst04[{idx}] = {val}".format(idx=i, val=lst04[i]))
运行结果：
归并排序
归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
分治法:
分割：递归地把当前序列平均分割成两半。
集成：在保持元素顺序的同时将上一步得到的子序列集成到一起（归并）。
这是归并排序的动图示例：
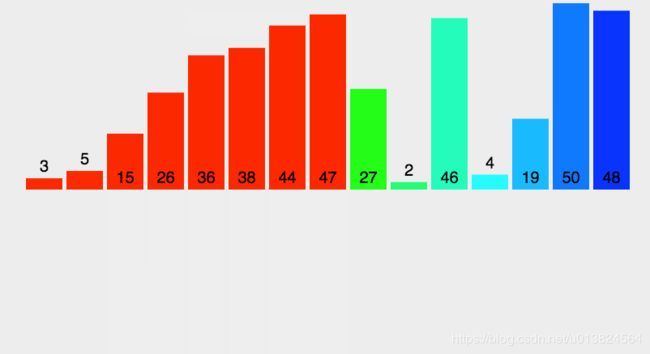
我这里的图不会动，想看动图示例到这里看：Python 归并排序
大家可以查看这个网址，有图例展示归并排序的过程。
Python 归并排序
def merge(arr, l, m, r):
n1 = m - l + 1
n2 = r - m
L = [0] * (n1)
R = [0] * (n2)
for i in range(0, n1):
L[i] = arr[l + i]
for j in range(0, n2):
R[j] = arr[m + 1 + j]
i = 0
j = 0
k = l
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
while i < n1:
arr[k] = L[i]
i += 1
k += 1
while j < n2:
arr[k] = R[j]
j += 1
k += 1
def mergeSort(arr, l, r):
if l < r:
m = int((l + (r - 1)) / 2)
mergeSort(arr, l, m)
mergeSort(arr, m + 1, r)
merge(arr, l, m, r)
arr = [12, 11, 13, 5, 6, 7, 9, 234, 23, 123, 45]
n = len(arr)
print("给定的数组")
for i in range(n):
print("%d" % arr[i]),
mergeSort(arr, 0, n - 1)
print("\n\n排序后的数组")
for i in range(n):
print("%d" % arr[i])
运行结果：
堆排序
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。
示意图：
可以看这里，查看动态堆排序示意图：
Python 堆排序
推荐代码一
def OneHeapSort(list1, l, r):
if r - l <= 0:
return
if r - l == 1 and list1[l] > list1[r]:
list1[l], list1[r] = list1[r], list1[l]
else:
middle = l + (r - l - 1) // 2
OneHeapSort(list1, l, middle)
OneHeapSort(list1, middle + 1, r - 1)
if list1[middle] > list1[r]:
list1[middle], list1[r] = list1[r], list1[middle]
if list1[r - 1] > list1[r]:
list1[r - 1], list1[r] = list1[r], list1[r - 1]
# 依次将最大值放到数组的后面
def heapSort(list):
for i in range(len(list) - 1, 0, -1):
OneHeapSort(list, 0, i)
list1 = [12, 11, 13, 5, 6, 7, 9, 234, 23, 123, 45]
heapSort(list1)
print(list1)
运行结果：
推荐代码二
def heapify(arr):
n = len(arr)
for i in reversed(range(n // 2)):
shiftDown(arr, n, i)
def shiftDown(arr, n, k):
while 2 * k + 1 < n:
j = 2 * k + 1
if j + 1 < n and arr[j + 1] < arr[j]:
j += 1
if arr[k] <= arr[j]:
break
arr[k], arr[j] = arr[j], arr[k]
k = j
def shiftDown2(arr, n, k):
smallest, l, r = k, 2 * k + 1, 2 * k + 2
while l < n:
if arr[l] < arr[smallest]:
smallest = l
if r < n and arr[r] < arr[smallest]:
smallest = r
if smallest == k:
break
else:
arr[k], arr[smallest] = arr[smallest], arr[k]
k = smallest
l, r = 2 * k + 1, 2 * k + 2
def heapSort(arr):
n = len(arr)
heapify(arr)
print("堆化：", arr)
for i in range(n - 1):
arr[n - i - 1], arr[0] = arr[0], arr[n - i - 1]
# print("交换最小值后：",arr)
shiftDown(arr, n - i - 1, 0)
# print("调整后：",arr)
arr = [12, 11, 13, 5, 6, 7, 9, 234, 23, 123, 45]
heapSort(arr)
print("排序后：", arr)
运行结果：
这两种方式有不同特点，还是挺易于理解的。
·
·
·
希尔排序
大家可以参考这里：
Python 希尔排序
拓扑排序
大家可以参考这里：
Python 拓扑排序
