香农编码 哈夫曼编码 费诺编码的比较
文章目录
- 哈夫曼编码
- 编码步骤
- 例子
- 优点
- 缺点
- 费诺编码
- 编码步骤
- 例子
- 优点
- 缺点
- 香农编码
- 编码步骤
- 例子
- 优点
- 缺点
- 参考
备注:本文除了例子与数据,其他内容均为整合网络资源。
哈夫曼编码
编码步骤
S1 将信源符号按照概率大小从大到小排列;
S2 把概率最小的两个信源符号分成一组,其中,上面一个编码为0,下面一个编码为1,并将这两个符号的概率加起来,其结果再与尚未处理过的符号重新按照大小排序;
S3 重复步骤2,直到所有的信源符号都处理完毕;
S4 从右至左按照编码路径返回,即可得到各个码字。
例子
假设一信息源发出五个信号,每个信号的概率分布如下:
| 信号 | u1 | u2 | u3 | u4 | u5 |
|---|---|---|---|---|---|
| 概率 | 0.2 | 0.2 | 0.4 | 0.1 | 0.1 |
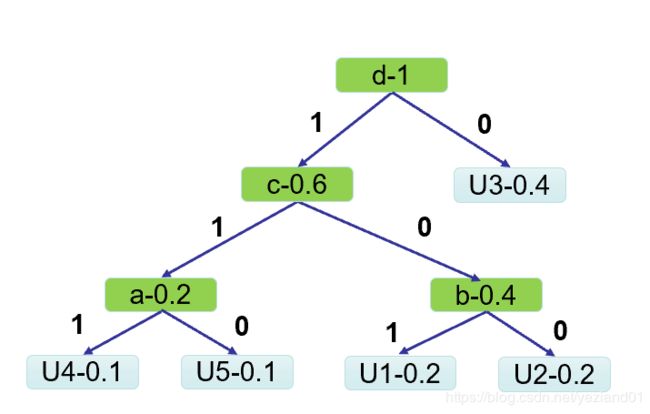
编码过程如下图:
输出码字:
| 信号 | u1 | u2 | u3 | u4 | u5 | 总和 |
|---|---|---|---|---|---|---|
| 概率 | 0.2 | 0.2 | 0.4 | 0.1 | 0.1 | |
| 码字 | 101 | 100 | 0 | 111 | 110 | |
| 码长 | 3 | 3 | 1 | 3 | 3 | |
| 平均码长 | 0.6 | 0.6 | 0.4 | 0.3 | 0.3 | 2.2 |
优点
== 赫夫曼码的码字(各符号的代码)是异前置码字,即任一码字不会是另一码字的前面部分。
== 赫夫曼码的各码字可以连在一起传送,中间不需另加隔离符号,只要传送时不出错,收端仍可分离各个码字,不致混淆。
== 当信息源各符号出现的概率很不平均的时候,哈夫曼编码的效果才明显。当信号源的符号概率为2的负幂次方时,达到100%的编码效率。
缺点
== 当信息源各符号出现的概率较为平均的时候,哈夫曼编码的效果不明显。
== 哈夫曼编码必须精确地统计出原始文件中每个符号的出现频率,如果没有这些精确的统计,将达不到预期的压缩效果。霍夫曼编码通常要经过两遍操作,第一遍进行统计,第二遍产生编码,所以编码速度相对慢。
== 编码长度不统一,硬件实现有难度。
== 由于编码长度可变。因此译码时间较长,使得霍夫曼编码的压缩与还原相当费时。
== 哈夫曼编码只能用整数来表示单个符号而不能用小数,这很大程度上限制了压缩效果。
== 哈夫曼所有位都是合在一起的,如果改动其中一位就可以使其数据变得面目全非。
费诺编码
编码步骤
S1 将信源符号按照其概率大小,从大到小排列;
S2 将这一组信源符号分成概率之和尽可能接近或者相等的一组(即两组分别的概率和之间的差尽可能小!);
S3 将上面一组符号编码成0,下面一组编码成1,反之亦可;
S4 将已经分好的组重复步骤2,3,直到不能再进行分组为止;
S5 从左到右一次写出码字。
例子
假设一信息源发出五个信号,每个信号的概率分布如下:
| 信号 | u1 | u2 | u3 | u4 | u5 |
|---|---|---|---|---|---|
| 概率 | 0.2 | 0.2 | 0.4 | 0.1 | 0.1 |
编码过程如下图:
输出码字:
| 信号 | u1 | u2 | u3 | u4 | u5 | 总和 |
|---|---|---|---|---|---|---|
| 概率 | 0.2 | 0.2 | 0.4 | 0.1 | 0.1 | |
| 码字 | 11 | 101 | 1 | 100 | 0 | |
| 码长 | 2 | 3 | 1 | 3 | 1 | |
| 平均码长 | 0.4 | 0.6 | 0.4 | 0.3 | 0.1 | 1.8 |
优点
== 比较适合于对分组概率相等或接近的信源编码
== 考虑了信源的统计特性,使概率大的信源符号能对应码长较短的码字,从而有效地提高了编码效率。
缺点
== 不一定是最佳码。因为费诺编码方法不一定能使短码得到充分利用。当信源符号较多时,若有一些符号概率分布很接近,分两大组的组合方法就会很多。可能某种分大组的结果,会使后面小组的“概率和”相差较远,从而使平均码长增加。
香农编码
编码步骤
S1 将q个信源符号按概率递减的方式进行排序:P1≥P2≥……Pq。
S2 按式-logP(Si)≤li≤1-logP(Si)(i=1,2,……q),计算出每个信源符号的码长li。
S3 为编成唯一可译码,计算第i个信源符号的累加概率。
S4 将累加概率Gi用二进制表示。
S5 取Gi对应二进制数的小数点后li位构成该信源符号的二进制码字。
例子
假设一信息源发出五个信号,每个信号的概率分布如下:
| 信号 | u1 | u2 | u3 | u4 | u5 |
|---|---|---|---|---|---|
| 概率 | 0.2 | 0.2 | 0.4 | 0.1 | 0.1 |
编码过程如下表:
| 信号 | 概率 | 累加概率 | 二进制小数 | -log(2)p | 码长 | 码字 | 平均码长 |
|---|---|---|---|---|---|---|---|
| u3 | 0.4 | 0 | 0.00… | 1.321928095 | 2 | 00 | 0.8 |
| u1 | 0.2 | 0.4 | 0.011… | 2.321928095 | 3 | 011 | 0.6 |
| u2 | 0.2 | 0.6 | 0.100… | 2.321928095 | 3 | 100 | 0.6 |
| u4 | 0.1 | 0.8 | 0.1100… | 3.321928095 | 4 | 1100 | 0.4 |
| u5 | 0.1 | 0.9 | 0.1110… | 3.321928095 | 4 | 1110 | 0.4 |
| 总和 | 2.8 |
输出码字:
| 信号 | u1 | u2 | u3 | u4 | u5 |
|---|---|---|---|---|---|
| 码字 | 011 | 100 | 00 | 1100 | 1110 |
优点
== 有重要的理论意义。
缺点
== 编码效率不高。
== 其平均码长不是最短的。
== 冗余度稍大,实用性不大。
== 由于码长总是进一取整,香浓编码方法不一定是最佳的。
参考
https://blog.csdn.net/yongf2014/article/details/46573557 信源编码算法(费诺编码&&哈夫曼编码)
https://wenku.baidu.com/view/401ee543a417866fb84a8e6f.html 信息论与编码–费诺编码与哈弗曼编码比较