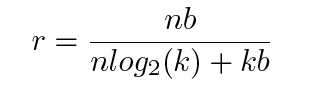网络模型剪枝-论文阅读-Deep compression

下载地址：《Deep compression: Compressing deep neural networks with pruning, trained quantization and Huffman coding》

这篇是韩松大神的代表作，是ICLR2016年的best paper，值得好好读一下。

其实这篇论文本质上是《Learning both Weights and Connections for Efficient Neural Networks》的极致扩展，是在这篇论文基础上继续压缩模型，建议先看下该篇论文的讲解。

Introduction

论文首先从存储大小和能量消耗的角度表明现有大模型的缺点，然后引出论文的目标：降低网络模型的存储和能量消耗使得这些模型能更好地部署到移动端。所以论文提出了Deep Compression，包括三个步骤，如下图：

首先，对网络进行剪枝并且保留剪枝前的精度；然后，对权重进行量化，使得多个连接能共享同一个权重，从而可以使用更加有效的存储方式；最后，使用霍夫曼编码（Huffman coding）压缩权重。

网络剪枝

这里的网络剪枝是完全按照《Learning both Weights and Connections for Efficient Neural Networks》这篇论文进行的，所以就不详述方法了。通过剪枝，可以分别减少AlexNet和VGG-16网络的9X和13X的参数。

剪枝后的网络是稀疏结构，所以需要特殊的存储方式，文中使用的是compressed sparse row(CSR)或compressed sparese column(CSC）方式，只需要2a+n+1个数字即可存储，其中a是非零数字的个数、n是行数或列数（感兴趣的可以看下说明，一般实现是用scipy.sparse.csr_matrix实现）。

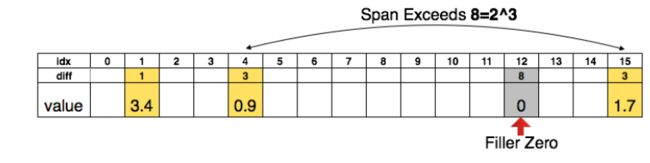
为了更进一步压缩，文中还对数据的索引进行了压缩，对卷积层和FC层分别使用8bits和5bits压缩。如图所示是3bits压缩方式，

该图有点不直观，简单来说就是对于3.4这个值，它的idx为1，而上一个索引是0，所以它的diff=1-0=1；

对于idx为4、value为0.9的这个值，它与上一个索引（即idx为1、值为3.4的索引）的差距diff=4-1=3；

对于idx为15、value为1.7的值，由于它与上一个索引（idx=4）的diff（15-4=11）超过了3bits（2^3=8)，所以在idx=12处加了一个diff=8，然后idx=15处的diff就等于3了。

量化训练和权重共享

网络量化就是指将本来32bits的数据量化到16bits、8bits甚至1bits，权重共享是指多个网络连接使用共享同一个权重。

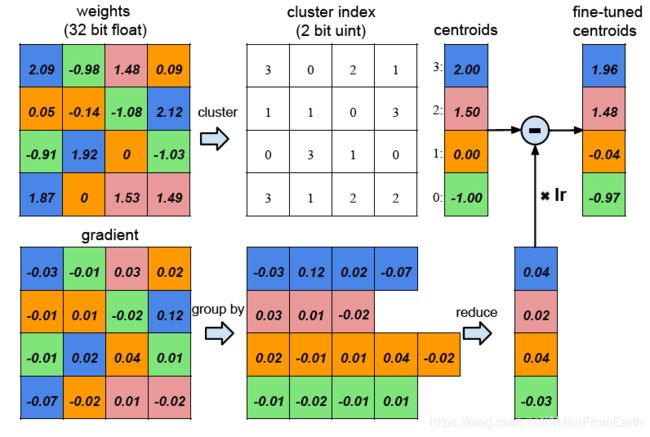
如下图所示是权重共享示意：

对于一个4x4的权重矩阵来说，将它的所有权重进行量化后聚类成4个centroid（使用不同的颜色标注），同一个centroid的所有权重共享同一个权重，所以为了存储对应关系，需要一个4x4的cluster index矩阵来存储。在反向传播过程中，同一个centroid的所有的权重的梯度相加然后乘以学习率lr更新centroids。

对于AlexNet来说，可以将每层卷积层量化为8bits（256个共享权重）和每层FC层量化为5bits（32个共享权重）的同时不损失精度。

文中还给出了压缩比例计算公式：

其中，k是聚类数目，cluster index矩阵需要${\log }_2(k)$bits，n表示所有连接数，每个连接占用b个bits。

以上图举例，共有16个连接权重，聚类中心为4个。原始的权重是32bits，index矩阵需要16个2-bit大小，所以压缩比例r = 16 * 32 / (16 * 2 + 4 * 32) = 3.2。

权重共享

文中使用k-means聚类方法来确定哪些权重可以共享一个centroid，这个比较基础，就不多说了，实现方式可以用sklearn.cluster.KMeans。

共享权重初始化（即选择聚类中心）

文中比较了3种不同的聚类中心初始化方式：随机、基于分布密度、线性。

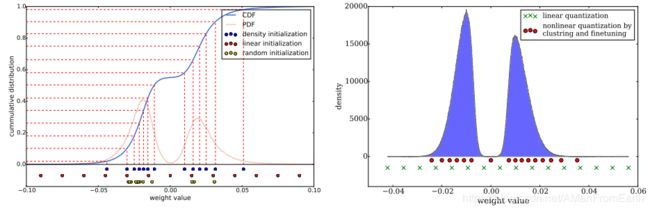
如图所示，剪枝后的权重分布呈现双正态分布状态。

随机：由于权重多在正态分布的峰值位置，所以随机初始化倾向于选择峰值位置的点作为聚类中心（左图黄点）；

基于分布密度：如图中蓝色线是累计分布函数CDF曲线，按照相同的间隔取值作为聚类中心（左图蓝点），结果也是在峰值位置，但是比随机初始化更加分散；

线性：对权重的[min,max]区间进行线性划分（左图红点），该划分与权重分布无关。

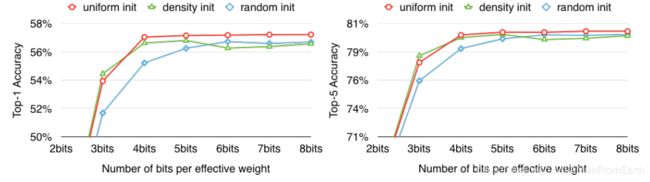
在之前的剪枝介绍中有一个重要的剪枝前提就是权重越大的连接越重要，但是这些连接较少。所以随机和基于分布密度的初始化方式中很少有聚类中心能落到这些点附近，使得聚类中心对这些重要的权重表现能力差。但是线性初始化并不存在上述问题。同时在实验中也证明了上述结论，如下图：

霍夫曼编码

霍夫曼编码是一种非常常见的压缩方式，这里也不赘述了。实验证明，霍夫曼编码能节省20%-30%的网络存储。

实验

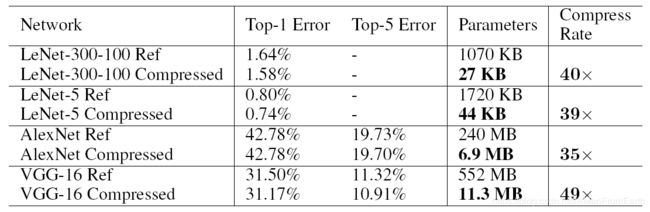
实验结果还是非常惊人的，如下图：

可以看出，对于VGG-16来说，压缩49X的时候还能保持原有精度。

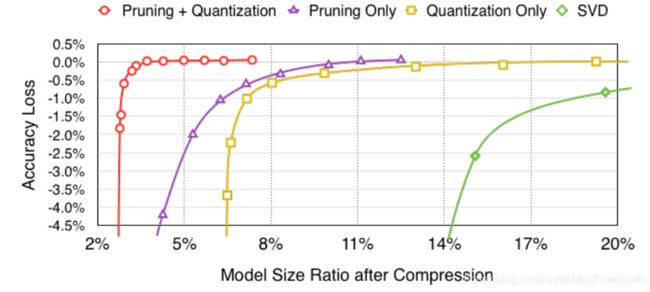
同时也实验了剪枝和量化压缩方法之间的关系，如下图：

可以看出，当剪枝或量化单独进行时，在保持原有精度的时候压缩比较低；但是当一起压缩时，压缩比能提升很大幅度。

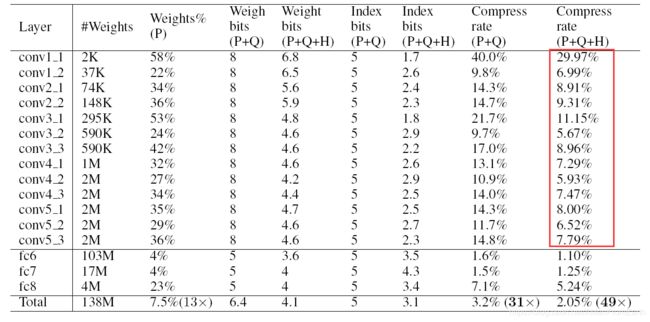
但是该方法依然存在缺点，如对于卷积层压缩程度不够（见下图）以及需要特殊的方式才能保存压缩后的网络模型。

以上就是本文的全部内容了。实际上该论文经典是指出了一条成熟极致压缩的pipeline，即剪枝-量化-编码，即使现在来看其方法较为落后，但是其路线依然能套到其他方法中使用，贡献巨大。