MNIST机器学习入门（下篇）

---

MNIST手写数字识别（卷积池化）

一 前言

  在本博客之前，关于采用Softmax回归模型实现MNIST手写数字，在小编的另一篇博客：MNIST手写数字识别（Softmax回归）已经进行了阐述，感兴趣的小伙伴可以看看。在本博客中，小编主要总结采用CNN网络实现手写数字识别过程中自己的一些收获。

二 基本概念

1. 卷积 Convolution

  小编想用一句话概括卷积操作：在已规定卷积核大小、个数、步长的基础上，对图片进行特征提取，并最终生成feature map的过程。 n个卷积核，意味着从n个不同的角度去观察图片，提取这个角度发现的特征，并最终生成 n 个feature map (特征图)，卷积操作后输出的特征图的数量和卷积核的数量是相同的。

  先来解释上图：输入图片为RGB三色，也就是channels通道数为3，采用了两个filter卷积核，还有两个偏移量，最终生成2个特征图。最左边三个矩阵表示图片分解为RGB三色后每一种颜色的图片，中间6个3*3的矩阵表示两个卷积核W0和W1，中间下方两个方格表示偏移量，最右侧两个3 *3的矩阵表示输出的特征图。
  对于输入图片一般是4维的，[-1, 5, 5, 3]，每一个数字分别表示：图片的张数（-1表示张数不限）、图片的高度、图片的宽度、图片的通道数（若为灰度图，通道数为1，彩色图通道数为3），MNIST数据集中，输入图片的格式是[-1, 278]的形式，所以我们需要reshape转换成[-1, 28, 28, 1]的格式（只考虑灰度）。
  卷积核的表示也是4D的，[3, 3, 3, 2]，分别表示卷积核的高度宽度、卷积核对应的通道数，卷积核的个数。
  还有关于padding全零填充操作，padding一般有 ‘SAME’ 和 ‘VALID’ 两种选项，若padding = ‘SAME’，此时特征图大小的计算公式为：ceil (图片边长 / 卷积核步长)，所以当padding = ‘SAME’ && 卷积核步长 = 1时，特征图的size和原图片的size相同。 若padding = ‘VALID’，此时不进行边界全零填充，对于卷积核无法到达的图片的右侧或下侧，该部分图片信息将会丢失，对应特征图大小的计算公式为：ceil( (图片边长 - 卷积核边长 + 1) / 卷积核步长 ) 。一般来说，在卷积操作时padding常采用SAME，在池化操作时，常采用VALID，并且在图片边界填充多少行列的0，这件事是有卷积本身选择的。
  由上图可以得到，卷积核的步长为2，并且padding 采用SAME选项，我们来看一下计算的流程，同一个卷积核的三个维度与图片RGB三色图片矩阵的对应位置分别相乘相加，所以得到第一个特征图的第一个数字为4 + 0 + 1 + 1 = 6，之后卷积核向右移动2个步长，同理进行计算。
  大家需要注意的是，卷积操作中的卷积核就是我们之前说的W权值，训练模型，其实就是不断优化修改卷积核和偏移量中的值，所以说，一开始我们通常对卷积核和偏移量随便进行初始化赋值就行 (但不可以为全0，好像是对梯度有影响) 。

• 关于卷积的练习代码

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.datasets import load_sample_images

# 加载数据集
# 输入的图片通常是3D [height, width, channels]
# mini-batch 通常是4D [mini-batch size, height, width, channels]
dataSet = np.array(load_sample_images().images, dtype=np.float32)
batch_size, height, width, channels = dataSet.shape
print(batch_size, height, width, channels)
# 2 427 640 3
# 输出说明有2张图片，图片的高度和宽度为427、640，图片显然是彩色的通道数为3

# 创建两个卷积核
# filter 中分别表示: height, width, channels, 卷积核个数
filter_test = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filter_test[3, :, :, 0] = 1   # 第一个卷积核 水平
filter_test[:, 3:, :, 1] = 1  # 第二个卷积核 竖直

# 卷积操作，得到卷积后的feature map
X = tf.placeholder(dtype=tf.float32, shape=(None, height, width, channels))
# 步长strides=[1, 2, 2, 1] 第一个和最后一个固定为1，中间两个数表示在行和列上对应的步长
conv = tf.nn.conv2d(X, filter=filter_test, strides=[1, 2, 2, 1], padding="SAME")

# 在会话中启动操作
with tf.Session() as sess:
    output = sess.run(conv, feed_dict={X: dataSet})

print(type(output))
print(output.shape)
print(output[0])

# 展示原图
plt.imshow(load_sample_images().images[0])
plt.show()

# 展示第一层卷积之后的图
plt.imshow(output[0, :, :, 1])
plt.show()

2. 池化 Pooling

  同样一句话概括池化操作：实质上就是一个降采样subsample的过程，将卷积操作输出的feature map作为池化层的输入，选取feature map中的一些信息，舍弃另一些信息，从而减少计算量，并且减少过拟合现象的产生。
  池化操作同样也是通过一个池化核，进行信息的提取，池化操作分为两种：最大池化和平均池化。（在卷积操作中卷积核就是我们要求的W权值，在池化操作中池化核只是一个选择的工具，选择池化核所在图片范围内的最大值或者是所有值的平均值）

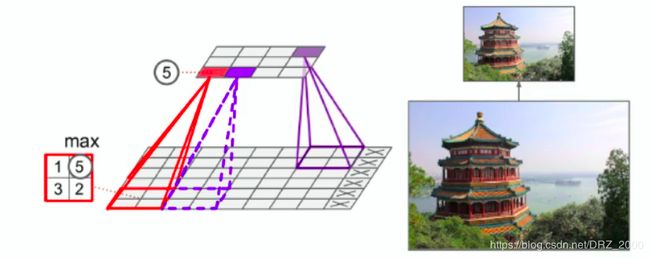
  上面我们说到在pooling中padding常采用VALID选项，我们知道VALID选项不采用全0填充，所以因为池化核步长的关系，图片右侧或者是下方部分的信息可能会丢失，而我们池化操作本来就是要丢掉一些东西的，所以无伤大雅。
  最大池化，在小编看来就是在该区域中提取最鲜明的特征，保留该特征，并舍弃其他不鲜明的特征；平均池化，求出该区域所有像素点灰度的平均值，所以应该是将该区域模糊化。

3. 激活函数 Activation Function

  在MNIST手写数字识别中采用的激活函数是ReLU函数，关于激活函数的定义，激活函数的作用，是否可以没有激活函数，这些问题，一一回答，首先激活函数是必要的，若是没有激活函数，模型的学习能力将会大打折扣，激活函数使得我们的模型具有非线性建模的能力，没有激活函数，即使神经网络的深度再深，网络实现的只是一个线性的映射，它都可以等价于深度为1的一个线性映射，而无法实现非线性分布的数据的映射。关于激活函数的种类，有很多: Sigmoid函数、ReLU函数、tanh函数等等，这里直接分享一片链接：深度学习中的激活函数，小编就不再多说了。

4. 全连接层 Fully Connected Layer

  全连接层（fully connected layers，FC）在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。
  全连接的核心操作就是矩阵向量乘积 y = Wx, 本质就是由一个特征空间线性变换到另一个特征空间。目标空间的任一维——也就是隐层的一个 cell——都认为会受到源空间的每一维的影响。不考虑严谨，可以说，目标向量是源向量的加权和。
  在 CNN 中，全连接常出现在最后几层，用于对前面设计的特征做加权和。比如 mnist，前面的卷积和池化相当于做特征工程，后面的全连接相当于做特征加权。

三 代码实现

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('MNIST_data_bak/', one_hot=True)
sess = tf.InteractiveSession()


# 截断的正态分布噪声，标准差设为0.1
# 同时因为我们使用ReLU作为激活函数，给偏置项加一些小的正值0.1 来避免死亡结点(dead neurons)
def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


# 卷积和池化接下来需要重复使用，故创建函数方便调作用
# tf.nn.conv2d()函数是TensorFlow中的2维卷积函数，其中x为输入，W为卷积核，例如[5, 5, 1, 32]
# 前面两个数字表示卷积核的size，第三个数字标识channel通道数，由于只是灰度图，所以为1
# 最后一个数字32表示卷积核的数量，表示从32个不同的角度分别提取图片的特征
# 最后获得的feature map的数量和卷积核的数量相同
# 此处strides=[1, 1, 1, 1]，同时padding='SAME'，所以最后的feature map的大小和原图片相同
def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')


# tf.nn.max_pool()函数是TensorFlow中的最大池化函数，这里我们使用2x2的最大池化
# 除了最大池化，还有平均池化，最大池化是在2x2的区域中选择值最大的像素点，保留最显著的特征
# 平均池化，将区域中的像素加和求平均值，也就是将该区域中的图片模糊化
# pooling只是一个subsample的过程，所以没有W参数，同时池化减少信息量，可以减少过拟合现象的发生
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')


# 卷积神经网络会利用空间信息，所以将1D的输入向量转化为2D向量，也就是从1*784转换为28*28
# 同时因为颜色通道数为1，所以最终的尺寸为[-1, 28, 28, 1]，-1表示图片的数量无限
x = tf.placeholder(tf.float32, shape=[None, 784])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
x_image = tf.reshape(x, shape=[-1, 28, 28, 1])

# 第一层卷积
# 我们使用32个卷积核，每个卷积核的size为5*5，并且通道数为1，其中W和b均使用之前定义好的函数初始化
# 使用conv2d()函数进行卷积操作，之后加上偏移量
# ReLU激活函数实现非线性处理，最后采用最大池化函数对卷积的输出结果进行池化操作
# 由x_image和W_conv1可知，卷积操作完成后得到32个size=28*28,通道数为1的feature map
# 之后进行2x2的池化操作，feature map的个数不变，但是图片的size变成14*14
# 最终得到的结果作为下一层卷积的输入
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
print("h_pool1.shape = {}".format(h_pool1.shape))

# 第二层卷积
# 操作和第一层卷积一致，只是卷积核发生变化，通道数变为32，和上一层的feature map的个数相同
# 一般卷积核的个数相对于上一次的卷积核个数翻倍
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
print("h_pool2.shape = {}".format(h_pool2.shape))

# 之前使用了两次2*2的最大池化，所以边长只有原来的1/4， 图片尺寸从28*28变成7*7
# 第二次使用卷积核的个数为64，所以最终得到的tensor尺寸为7*7*64
# 后面我们接一个全连接层，隐含的结点为1024个，并使用ReLU激活函数
# 我们使用tf.reshape()函数对第二层卷积输出的tensor进行变形，将其转换为1D的向量
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# 防止过拟合，使用Dropout层
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

# 接 Softmax分类
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

# 定义交叉熵损失函数
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv), reduction_indices=[1]))
optimizer = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# 训练
tf.global_variables_initializer().run()
for i in range(20000):
    batch = mnist.train.next_batch(50)
    if i % 100 == 0:
        train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
        print("step %d, training accuracy %g" % (i, train_accuracy))
    optimizer.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

print("test accuracy %g" % accuracy.eval(
    feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

关于代码说明，程序中有详细的注释，这里不再赘述。

四 关于神经网络的一些知识

CNN 卷积神经网络，全称：convalutional neural network
DNN 深度神经网络，全称：deep neural network
RNN 循环神经网络，全称：recurrent neural network

---

关于CNN网络的一些典型的模型：

1. LeNet-5架构， 1998
2. AlexNet， 2012
3. GoogLeNet, 2014
4. ResNet, 2015

---

CNN网络的一般架构

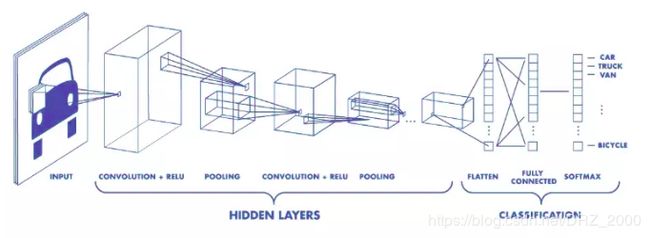
input输入层 + 若干个(卷积 + 激活 + 池化) + 若干全连接层 + output输出层
在MNIST中还有Softmax层实现概率分配。

---

其实小编在机器学习方面很白，约等于白板，可是谁让小编和晴雯一样，虽然命比纸薄，但心比天高 :<(, wu~~~~~~，加油，谁都是这样过来的，路漫漫其修远兮，吾将上下而求索！！！加油，与君共勉！