LeNet5卷积神经网络paper学习笔记

微信公众号：小白图像与视觉

关于技术、关注yysilence00。有问题或建议，请公众号留言。

---

主题：LeNet5卷积神经网络paper学习笔记

详情请点击 LeNet-5

一、介绍

LeNet5诞生于1994年，是最早的卷积神经网络之一，推动了深度学习领域的发展。自从1988年开始，在多年的研究和许多次迭代后，这项由Yann LeCun大神完成的开拓性成果,被命名为LeNet5。

介绍之前让我们先来熟悉一下卷积层和池化层

LeNet-5中主要有2个卷积层、2个下抽样层（池化层）、3个全连接层3种连接方式

LeNet-5卷积层(conv层)
卷积层采用的都是5x5大小的卷积核/过滤器（kernel/filter），且卷积核每次滑动一个像素（stride=1），一个特征图谱使用同一个卷积核.
每个上层节点的值乘以连接上的参数，把这些乘积及一个偏置参数相加得到一个和，把该和输入激活函数，激活函数的输出即是下一层节点的值

LeNet-5的下采样层（pooling层）
下抽样层采用的是2x2的输入域，即上一层的4个节点作为下一层1个节点的输入，且输入域不重叠，即每次滑动2个像素，下抽样节点的结构如下

二、LeNet-5 网络逐层解析

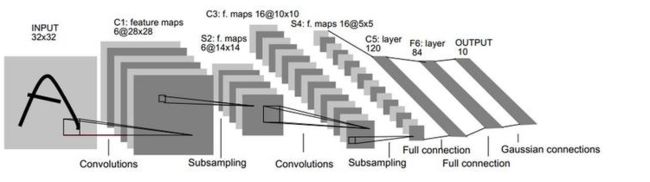LeNet-5

• LeNet-5包含了3层卷积、2层池化、2层全连接
• 具体来讲即input-C1-S2-C3-S4-C5-F6-output

0、INPUT层-输入层

该网络目的是手写字母或者数字，如邮编，的识别问题，实际上就是一个已知所有字符模式的一个匹配，或者分类的问题。因为从MNIST上测试，也就是说，图片输入大小为28×28，这里首先把输入做成32×32默认灰色图片单通道，把28的图像放在中间，目的是在第一层做5×5的convolution提取特征的时候，边角的位置的特征也能被提取到，因为一次5×5过后，32就变成了28（也就是现在常说的convolution的mode中full，same，valid的valid模式）。
首先是手写数据 INPUT 层，输入图像的尺寸统一归一化为32*32。

输入图片：32*32

1、C1层-卷积层(convolutions卷积层)

C1 层是一个卷积层，由 6 个特征图 Feature Map 构成。特征图中每个神经元与输入为 5x5 的邻域相连。特征图的大小为 28x28，这样能防止输入的连接掉到边界之外（32-5+1=28）。C1 有 156 个可训练参数（每个滤波器5x5=25个 unit 参数和一个 bias 参数，一共 6 个滤波器，共(5x5+1)x6=156个参数），共 156x(28x28)=122304 个连接。

上层输入大小：32*32

卷积核size: 5*5

卷积核数目： 6

输出featuremap大小：28*28 （32-5+1）=28

神经元数量：28286

可训练参数：（5*5+1) * 6（每个滤波器5*5=25个unit参数和一个bias参数，一共6个滤波器）

连接数：（55+1）62828=122304

2、S2层-池化层（subsampling下采样层）

S2 层是一个下采样层，有 6 个14x14 的特征图。特征图中的每个单元与 C1 中相对应特征图的 2x2 邻域相连接。S2 层每个单元的 4 个输入相加，乘以一个可训练参数，再加上一个可训练偏置。每个单元的 2x2 感受野并不重叠，因此 S2 中每个特征图的大小是 C1 中特征图大小的 1/4（行和列各1/2）。S2 层有12（6x（1+1）=12）个可训练参数和 5880（14x14x（2x2+1）x6=5880）个连接。
得到了6个28×28的feature map，对这些fm也就是C1层做降采样得到s2，这里的降采样和max pooling等不太一样，它的做法是这样：采样后的fm的每个像素都只和上面的2×2的邻域有关，首先把对应于S2中一个unit 的四个input相加，然后给它们乘上一个可以训练的系数，再加上bias，然后过一个sigmoidal的激励函数。2×2的receptive field是不重叠的，这和pooling是一致的。这样就得到了14×14的6个fm，也就是S2。

输入：28*28

采样区域：2*2

采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid

采样种类：6

输出featureMap大小：14*14（28/2）

神经元数量：14146

可训练参数：（1+1) * 6 = 12

连接数：（2 * 2 + 1）* 6 * 14 * 14

3、C3层-卷积层（(convolutions卷积层）

C3 层也是一个卷积层，它同样通过 5x5 的卷积核去卷积层 S2，然后得到的特征 map 就只有 10x10 个神经元，但是它有 16 种不同的卷积核，所以就存在 16 个特征 map 了。 C3 中每个特征图由 S2 中所有 6 个或者几个特征 map 组合而成。为什么不把 S2 中的每个特征图连接到每个 C3 的特征图呢？原因有 2 点。第一，不完全的连接机制将连接的数量保持在合理的范围内。第二，也是最重要的，其破坏了网络的对称性。由于不同的特征图有不同的输入，所以迫使他们抽取不同的特征（希望是互补的）。

例如，存在的一个方式是：C3 的前 6 个特征图以 S2 中 3 个相邻的特征图子集为输入。接下来 6 个特征图以 S2 中 4 个相邻特征图子集为输入。然后的 3 个以不相邻的 4 个特征图子集为输入。最后一个将 S2 中所有特征图为输入。这样 C3 层有1516（6x（3x25+1）+6x（4x25+1）+3x（4x25+1）+（25x6+1）=1516）个可训练参数和151600（10x10x1516=151600）个连接。
然后对S2再做convolution，仍然是5×5，但是这里需要注意，C3中的每个fm不是和S2中所有的fm都有连接的。column对应的是上一层的6个，row对应于下一层的16个。可以看出，这16个里，前面的6个，即0–5，是由相邻的三个fm组合变换而成，而中间的6个，即6-11，是相邻的四个fm，而再后面的三个是不相邻的四个fm，最后一个，即15，是所有的fm都连接得到的。

为何要采用这样的连接。作者给出两点理由：首先，可以降低连接数目（毕竟当时还没有这么多框架和GPU，参数量规模不要过大还是一个需要考虑的因素）；另外，更重要的一个理由是，作者希望通过这种方式学得一个可以互补的fm，通过强行破坏网络结构中，也就是上下层连接中的这种对称性。这样可以得到C3。

输入：S2中所有6个或者几个特征map组合

卷积核大小：5*5

卷积核种类：16

输出featureMap大小：10*10 (14-5+1)=10

可训练参数：6(355+1)+6(455+1)+3(455+1)+1(655+1)=1516

连接数：10101516=151600

4、S4层-池化层（subsampling下采样层）

输入：10*10

采样区域：2*2

采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid

采样种类：16

输出featureMap大小：5*5（10/2）

神经元数量：5516=400

可训练参数：（1+1) * 16 = 32

连接数：16（22+1）55=2000

S4中每个特征图的大小是C3中特征图大小的1/4

5、C5层-卷积层（(convolutions卷积层）

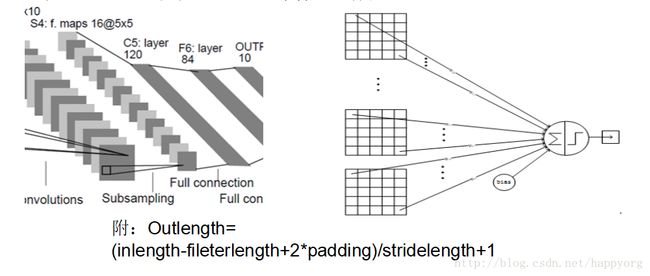
C5 层是一个卷积层(有的地方也称该层为连接层)，有 120 个特征图。每个单元与 S4 层的全部 16 个单元的 5x5 邻域相连。由于 S4 层特征图的大小也为 5x5（同滤波器一样），故 C5 特征图的大小为 1x1（5-5+1=1）：这构成了 S4 和 C5 之间的全连接。之所以仍将 C5 标示为卷积层而非全连接层，是因为如果 LeNet-5 的输入变大，而其他的保持不变，那么此时特征图的维数就会比 1x1 大。C5 层有 48120（120x（16x5x5+1）=48120 个可训练连接。

输入：S4层的全部16个单元特征map（与s4全相连）

卷积核大小：5*5

卷积核种类：120

输出featureMap大小：1*1（5-5+1）

可训练参数/连接：120（165*5+1）=48120

6、F6层-全连接层（full connection）

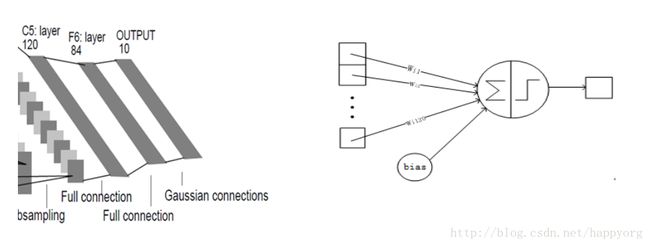
F6 层有 84 个单元（之所以选这个数字的原因来自于输出层的设计），与 C5 层全相连。有10164（84x(120x(1x1)+1)=10164）个可训练参数。如同经典神经网络，F6 层计算输入向量和权重向量之间的点积，再加上一个偏置。然后将其传递给sigmoid函数产生单元i的一个状态。

输入：c5 120维向量

输出：F6 84维向量

计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出。

可训练参数/连接:84*(120+1)=10164

7、Output层-全连接层（full connection）

Output层也是全连接层，共有10个节点，分别代表数字0到9，且如果节点i的值为0，则网络识别的结果是数字i。采用的是径向基函数（RBF）的网络连接方式。假设x是上一层的输入，y是RBF的输出，则RBF输出的计算方式是：

上式w_ij 的值由i的比特图编码确定，i从0到9，j取值从0到7*12-1。RBF输出的值越接近于0，则越接近于i，即越接近于i的ASCII编码图，表示当前网络输入的识别结果是字符i。该层有84x10=840个参数和连接。

输入：F6 84维向量

输入：10维向量

可训练参数/连接:84*(10)=840

三、总结

• 卷积网络在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，而不需要任何输入和输出之间的精确的数学表达式。

• LeNet-5是一种用于手写体字符识别的非常高效的卷积神经网络。通过对LeNet-5的网络结构的分析，可以直观地了解一个卷积神经网络的构建方法，可以为分析、构建更复杂、更多层的卷积神经网络做准备。

• LaNet-5的局限性
  CNN能够得出原始图像的有效表征，这使得CNN能够直接从原始像素中，经过极少的预处理，识别视觉上面的规律。然而，由于当时缺乏大规模训练数据，计算机的计算能力也跟不上，LeNet-5 对于复杂问题的处理结果并不理想。

• 2006年起，人们设计了很多方法，想要克服难以训练深度CNN的困难。其中，最著名的是 Krizhevsky et al.提出了一个经典的CNN 结构，并在图像识别任务上取得了重大突破。其方法的整体框架叫做 AlexNet，与 LeNet-5 类似，但要更加深一些。

参考文献：
1、LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278-2324.

2、https://blog.csdn.net/edogawachia/article/details/79962045

3、https://blog.csdn.net/happyorg/article/details/78274066

更多请参考：