剑指offer刷题记录
说明
剑指offer刷题笔记,1~40题,
https://www.nowcoder.com/ta/coding-interviews?page=1
二维数组中的查找
题意:
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
思路:
- 遍历每一行,每行二分查找,时间复杂度O( n l o g n nlogn nlogn)
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
for(int i = 0; i < array.size(); i++){
vector<int>::iterator it = lower_bound(array[i].begin(), array[i].end(), target);
if(it != array[i].end()){
int res = *it;
if(res == target){
return true;
}
}
}
return false;
}
};
- 由于从上到下递增,从左到右递增,那么从左下角开始找,比当前点小的往上,大的往右,要是越界就是找不到。
class Solution {
public:
bool Find(int target, vector<vector<int> > array) {
if (array.size() == 0){
return false;
}
int i = array.size() - 1, j = 0;
while(i >= 0 && i < array.size() && j >= 0 && j < array[0].size()){
if (target == array[i][j]){
return true;
}
if (target < array[i][j]){
i--;
continue;
}
if (target > array[i][j]){
j++;
}
}
return false;
}
};
替换空格
题意:
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
思路:
- 先从头到尾扫一边,看看一共多少空格 n n n,字符串长度扩充 n ∗ 3 n * 3 n∗3,定义扩充后的一个尾指针 p t a i l p_{tail} ptail,然后从尾往头扫一遍扩充前字符串,遇到普通字符直接放在 p t a i l p_{tail} ptail位置, p t a i l p_{tail} ptail向前移动一位,遇到空格, p t a i l p_{tail} ptail向前移动三位并放入%20
class Solution {
public:
void replaceSpace(char *str,int length) {
int cnt = 0, cntSpace = 0;
for(int i = 0; str[i]; i++){
if(str[i] == ' '){
cntSpace++;
}
cnt = i;
}
str[cnt+cntSpace*2+1] = '\0';
int r = cnt+cntSpace*2, end = cnt;
while(end >= 0){
if(str[end] != ' '){
str[r] = str[end];
r--, end--;
}else{
str[r--] = '0';
str[r--] = '2';
str[r--] = '%';
end--;
}
}
}
};
从尾到头打印链表
题意:
输入一个链表,按链表从尾到头的顺序返回一个ArrayList。
思路:
- 由于返回的是数组而不是同指针,不需逆转链表操作,而是顺序将链表存数组,然后数据再反转返回就OK
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) :
* val(x), next(NULL) {
* }
* };
*/
class Solution {
public:
vector<int> printListFromTailToHead(ListNode* head) {
vector<int> res;
while(head){
res.push_back(head->val);
head = head->next;
}
for(int i = 0, j = res.size()-1; i < j; i++, j--){
swap(res[i], res[j]);
}
return res;
}
};
重建二叉树
题意:
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路:
由于二叉树前序后序的性质,明显前序第一个结点是当前树的根结点
- 对于中序序列,从中序找到前序的第一个结点位置 x x x,显而易见( / 狗 头 /狗头 /狗头), x x x左边的结点都为左子树,而且为左子树的中序 l e f t i n left_{in} leftin, x x x右边的结点都为右子树,而且为右子树的中序 r i g h t i n right_{in} rightin
- 对于前序序列,是先访问左再访问右,因此前n个数为左字数的前序,其中n为 l e f t i n left_{in} leftin的个数,其余为右边子数的前序
- 递归构造左右子树
- 注意点:构造子树的中序前序的时候记得要把当前前序的结点去掉
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
if (pre.size() == 0){
return NULL;
}
TreeNode* curNode = new TreeNode( pre[0]);
//left
vector <int> leftIn, leftPre;
//right
vector <int> rightIn, rightPre;
bool inLeft = true;
for (int i = 0; i < vin.size(); i++){
if (vin[i] == pre[0]){
inLeft = false;
continue;
}
if(inLeft){
leftIn.push_back(vin[i]);
}else{
rightIn.push_back(vin[i]);
}
}
//set leftInSet(leftIn.begin(), leftIn.end());
//set rightInSet(rightIn.begin(), rightIn.end());
for(int i = 1; i < pre.size(); i++){
if (i <= leftIn.size()){
leftPre.push_back(pre[i]);
}else{
rightPre.push_back(pre[i]);
}
}
curNode->left = reConstructBinaryTree(leftPre, leftIn);
curNode->right = reConstructBinaryTree(rightPre, rightIn);
return curNode;
}
};
用两个栈实现队列
题意:
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
思路:
- 简单的思路就是2个栈,先进后出,那么插入一个栈后把数据导入另外一个栈就Ok了,具体实现是插入的时候直接插入到栈1中,弹出的时候弹栈2,若栈2空了,把栈1里的东西全都吐给栈2
class Solution
{
public:
void push(int node) {
stack1.push(node);
}
int pop() {
if(stack2.empty() == false){
int res = stack2.top();
stack2.pop();
return res;
}
while(false == stack1.empty()){
stack2.push(stack1.top());
stack1.pop();
}
int res = stack2.top();
stack2.pop();
return res;
}
private:
stack<int> stack1;
stack<int> stack2;
};
旋转数组的最小数字
题意:
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
思路:
- 二分法,若中间的数 m m m大于左端的数,说明还在上升,最小的数在 m m m右边,若中间的数 m m m小于左端的数,说明开始下降了,最小的数在 m m m左边
class Solution {
public:
int minNumberInRotateArray(vector<int> rotateArray) {
if(rotateArray.size() == 0){
return 0;
}
int l = 0, r = rotateArray.size()-1;
vector<int> &arr = rotateArray;
int mid;
while(l < r){
mid = (l+r)/2;
if(arr[mid] < arr[r]){
r=mid;
}else if(arr[mid] >= arr[r]){
l=mid;
}
//cout<
if(r-l == 1){
return min(arr[r], arr[l]);
}
}
return arr[mid];
}
};
斐波那契数列
题意:
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。
n<=39
思路:
这题太无聊了,小学生题目,略
class Solution {
public:
int Fibonacci(int n) {
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
int a1 = 0, a2 = 1, res = 1;
for(int i = 1; i < n; i++){
res = a1+a2;
a1 = a2;
a2 = res;
}
return res;
}
};
跳台阶
题意:
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
思路:
- n n n级的跳法 f ( n ) f(n) f(n)为 f ( n − 1 ) + f ( n − 2 ) f(n-1) + f(n-2) f(n−1)+f(n−2),其实又是斐波那契数列
class Solution {
public:
int jumpFloor(int n) {
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
int a1 = 0, a2 = 1, res = 1;
for(int i = 1; i < n + 1; i++){
res = a1+a2;
a1 = a2;
a2 = res;
}
return res;
}
};
变态跳台阶
题意:
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路:
- 按照上题的思路,调到 n n n的跳法 f ( n ) f(n) f(n)有 f ( n ) = f ( n − 1 ) + f ( n − 2 ) + . . . + f ( 1 ) + 1 f(n) = f(n-1) + f(n-2) +...+f(1) + 1 f(n)=f(n−1)+f(n−2)+...+f(1)+1,1为直接跳到 n n n的方法
- f ( 1 ) = 1 f(1) = 1 f(1)=1
- f ( 2 ) = f ( 1 ) + 1 = 2 f(2) = f(1) + 1 = 2 f(2)=f(1)+1=2
- f ( 3 ) = f ( 1 ) + f ( 2 ) + 1 = 4 f(3) = f(1) + f(2) + 1 = 4 f(3)=f(1)+f(2)+1=4
- f ( 4 ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + 1 = 8 f(4) = f(1) + f(2) + f(3) + 1 = 8 f(4)=f(1)+f(2)+f(3)+1=8
- f ( 5 ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + f ( 4 ) + 1 = 16 f(5) = f(1) + f(2) + f(3) + f(4) + 1 = 16 f(5)=f(1)+f(2)+f(3)+f(4)+1=16
找规律,明显 f ( n ) = 2 ( n − 1 ) f(n) = 2^{(n-1)} f(n)=2(n−1)
顺便证明一下
f ( n ) = f ( n − 1 ) + f ( n − 2 ) + . . . + f ( 1 ) + 1 f(n) = f(n-1) + f(n-2) +...+f(1) + 1 f(n)=f(n−1)+f(n−2)+...+f(1)+1
f ( n − 1 ) = f ( n − 2 ) + . . . + f ( 1 ) + 1 f(n-1) = f(n-2) +...+f(1) + 1 f(n−1)=f(n−2)+...+f(1)+1
f ( n ) = 2 ∗ f ( n − 1 ) f(n) = 2*f(n-1) f(n)=2∗f(n−1) (这不就是等比数列的递推式?)
f ( n ) = 2 ∗ f ( n − 1 ) = 2 ∗ 2 ∗ f ( n − 2 ) = 2 3 ∗ f ( n − 3 ) = 2 n − 1 f(n) = 2*f(n-1) =2*2*f(n-2)=2^3*f(n-3)=2^{n-1} f(n)=2∗f(n−1)=2∗2∗f(n−2)=23∗f(n−3)=2n−1
class Solution {
public:
int jumpFloorII(int number) {
if(number == 0){
return 0;
}
return 1<<(number-1);
}
};
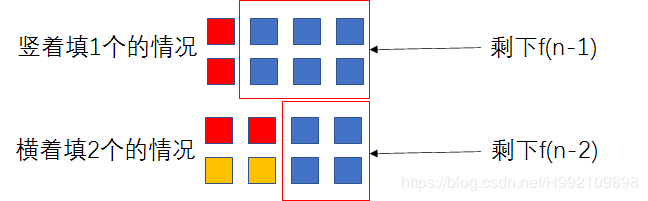
矩形覆盖
题意:
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
思路:
一开始为 f ( n ) f(n) f(n),反正都会填满,那么横竖2种情况为下图所述,于是,又是斐波那契数列
class Solution {
public:
int rectCover(int n) {
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
int a1 = 1, a2 = 2, res = 3;
for(int i = 2; i < n; i++){
res = a1+a2;
a1 = a2;
a2 = res;
}
return res;
}
};
二进制中1的个数
题意:
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
思路:
- 正数直接一直除2除到为0,负数直接转换为相应的正数再求
class Solution {
public:
int NumberOf1(int n) {
int res = 0;
if(n < 0){
res++;
n = INT_MAX + n + 1;
}
while(n>0){
if(n&1){
res++;
}
n =n>>1;
}
return res;
}
};
数值的整数次方
题意:
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。
保证base和exponent不同时为0
思路:
- 快速幂模板题,对于1个数 t t t的 n n n次方
- n n n为偶数,求 t n t^n tn,只要求 t n / 2 t^{n/2} tn/2再平方就可以了,比如 t = 2 , n = 8 t=2,n=8 t=2,n=8, 8 / 2 / 2 / 2 = 1 8/2/2/2 = 1 8/2/2/2=1, ( ( 2 2 ) 2 ) 2 = 2 8 ((2^2)^2)^2 = 2^8 ((22)2)2=28,都是3个2
- n n n为奇数,求 t n t^n tn,只要求 t n / 2 t^{n/2} tn/2再平方,再+1就可以了,比如 t = 2 , n = 9 t=2,n=9 t=2,n=9, 9 / 2 / 2 / 2 = 1 9/2/2/2 = 1 9/2/2/2=1,但是由于一开始9是奇数, ( 2 ∗ ( ( ( 2 ) 2 ) 2 ) 2 (2*(((2)^2)^2)^2 (2∗(((2)2)2)2,3个在外面的2,1个在里面的2
class Solution {
public:
double Power(double base, int exponent) {
double res = 1.;
bool less = false;
if(exponent < 0){
exponent = -exponent;
less = true;
}
while(exponent > 0){
if(exponent & 1){
res *= base;
}
base *= base;
exponent >>= 1;
}
if(less){
res = 1./res;
}
return res;
}
};
调整数组顺序使奇数位于偶数前面
题意:
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
思路:
- 从前往后扫
- 看见奇数继续扫
- 在位置 x x x看见偶数停下来往后找,找到奇数跟当前偶数交换?这样肯定不行的,这样若存在多个偶数连在一起,偶数的顺序就变了,那找到跟奇数相近的偶数交换?一直交换到位置 x x x,这样不如遇到一个偶数,往后数数偶数个数多少找到一个奇数 t t t, t t t直接向前移到位置 x x x,所有偶数靠后移。复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( 1 ) O(1) O(1)
说明:
- 肯定不能开辟新数组,没看见人家都传引用了吗
- 注意偶数向后查万一查到数组末尾那就结束了
class Solution {
public:
void reOrderArray(vector<int> &array) {
for(int i = 0; i < array.size(); i++){
if (array[i] % 2 == 1){
continue;
}
if (array[i] % 2 == 0){
int cntOdd = 0;
for(int j = i; j < array.size(); j++){
if (array[j] % 2 == 0){
cntOdd++;
}
else{
break;
}
}
if (i + cntOdd == array.size()){
break;
}
int temp = array[i + cntOdd];
for(int j = i + cntOdd; j > i; j--){
array[j] = array[j - 1];
}
array[i] = temp;
}
}
}
};
链表中倒数第k个结点
题意:
输入一个链表,输出该链表中倒数第k个结点。
思路:
- 链表从前到后扫一遍看看有几个节点,正数 节 点 数 − k 节点数-k 节点数−k个节点就完了, O ( n ) O(n) O(n)
class Solution {
public:
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
int cntNodeNum = 0;
for(ListNode *p1 = pListHead; p1; p1 = p1->next, cntNodeNum++);
int order = cntNodeNum - k;
for(ListNode *p1 = pListHead; p1; order--, p1 = p1->next){
if (order == 0){
return p1;
}
}
}
};
- 正常的解法是一个指针 p t a i l p_{tail} ptail先走K步,然后另外一个指针 p h e a d p_{head} phead再一起走, p t a i l p_{tail} ptail到结尾, p h e a d p_{head} phead就是所在位置
反转链表
题意:
输入一个链表,反转链表后,输出新链表的表头。
思路:
- 链表的题目都是无脑模拟,注意一下边界就可以了。
class Solution {
public:
ListNode* ReverseList(ListNode* pHead) {
if(pHead == NULL){
return pHead;
}
if(pHead->next == NULL){
return pHead;
}
ListNode* p0 = pHead;
ListNode* p1 = pHead->next;
if(pHead->next->next == NULL){
p1->next = p0;
p0->next = NULL;
return p1;
}
ListNode* p2 = p1->next;
pHead->next = NULL;
while(1){
p1->next = p0;
p0 = p1;
p1 = p2;
if(p1 == NULL){
return p0;
}
p2 = p1->next;
}
}
};
合并两个排序的链表
题意:
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
思路:
- 指针指向那个小的就可以了,定义一个头节点方便操作。
class Solution {
public:
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
ListNode* head = new ListNode(0);
ListNode* p0 = head;
ListNode* p1 = pHead1, *p2 = pHead2;
while(p1 || p2){
if(p1 == NULL){
p0->next = p2;
break;
}
if(p2 == NULL){
p0->next = p1;
break;
}
if(p1->val < p2->val){
p0->next = p1;
// cout<< p0->val << endl;
p0 = p0->next;
p1 = p1->next;
continue;
}
if(p1->val >= p2->val){
p0->next = p2;
// cout<< p0->val << endl;
p0 = p0->next;
p2 = p2->next;
continue;
}
}
return head->next;
}
};
树的子结构
题意:
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
思路:
- 递归操作,注意边界异常情况即可
class Solution {
public:
bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
{
if(pRoot1 == NULL || pRoot2 == NULL || pRoot1->val != pRoot2->val){
return false;
}
if(pRoot2->left == NULL && pRoot2->right == NULL){
return pRoot2->val == pRoot1->val;
}
if (pRoot1->val == pRoot2->val){
if(pRoot2->left == NULL && HasSubtree(pRoot1->right, pRoot2->right)){
return true;
}
if(pRoot2->right == NULL && HasSubtree(pRoot1->left, pRoot2->left)){
return true;
}
if(HasSubtree(pRoot1->left, pRoot2->left) && HasSubtree(pRoot1->right, pRoot2->right)){
return true;
}
}
return HasSubtree(pRoot1->left, pRoot2) || HasSubtree(pRoot1->right, pRoot2);
}
};
二叉树的镜像
题意:
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
思路:
- 直接模拟就是了,阿里实习面试题。。
class Solution {
public:
void Mirror(TreeNode *pRoot) {
if(pRoot == NULL){
return;
}
TreeNode *tmp = pRoot->left;
pRoot->left = pRoot->right;
pRoot->right = tmp;
Mirror(pRoot->left);
Mirror(pRoot->right);
}
};
顺时针打印矩阵
题意:
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
思路:
- 无脑模拟题,定义四个方向,手动模拟一下边界怎么操作就可以了。
class Solution {
public:
vector<int> printMatrix(vector<vector<int> > matrix) {
vector<int> res;
if (matrix.size() == 0){
return res;
}
if (matrix[0].size() == 0){
return res;
}
int i = 0, j = 0, dir = 0, mini = 0, maxi = matrix.size() - 1,
minj = 0, maxj = matrix[0].size() - 1;
while(res.size() < matrix.size() * matrix[0].size()){
res.push_back(matrix[i][j]);
if (dir == 0){
j++;
}else if(dir == 1){
i++;
}else if(dir == 2){
j--;
}else if (dir == 3){
i--;
}
if(dir == 0 && j > maxj){
dir = 1;
j--, i++;
mini++;
continue;
}
if(dir == 1 && i > maxi){
dir = 2;
i--, j--;
maxj--;
continue;
}
if(dir == 2 && j < minj){
dir = 3;
j++, i--;
maxi--;
continue;
}
if(dir == 3 && i < mini){
dir = 0;
i++, j++;
minj++;
continue;
}
}
return res;
}
};
包含min函数的栈
题意:
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
思路:
- 这题比较有趣,搞2个栈,另外一个存的时候存对应位置最小值,弹出时候一起弹就可以了
class Solution {
private:
int topP = 0;
vector <int> stack;
vector <int> minStack;
public:
void push(int value) {
if(topP < stack.size()){
stack[topP] = value;
if (topP == 0){
minStack[topP] = value;
}else{
minStack[topP] = std::min(minStack[topP-1], value);
}
}else{
stack.push_back(value);
if(minStack.size() == 0){
minStack.push_back(value);
}else{
int tmp = std::min(minStack[topP-1], value);
minStack.push_back(tmp);
}
}
topP++;
}
void pop() {
topP--;
}
int top() {
return stack[topP-1];
}
int min() {
return minStack[topP-1];
}
};