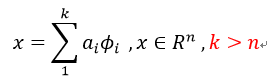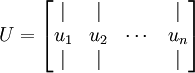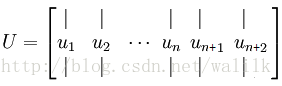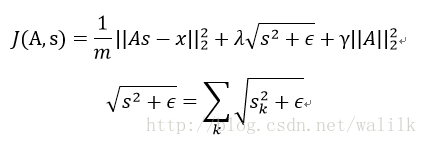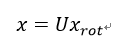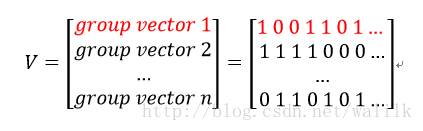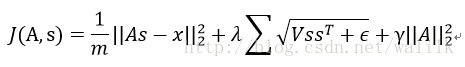深度学习模型---稀疏编码 Sparse Coding
前言
本文的理论部分主要整理自UFLDL的“Sparse Coding”章节和一些经典教材,同时也参考了网上的一些经典博客,包含了Sparse Coding的一些基本概念、优化方法、数学推导和应用场景,供读者参考。
![]()
预备知识
(1)稀疏线性模型
X为一个n为特征向量,可以是一个小波信号,可以是一副图片等。
D为标准化的基础矩阵,由组成元素的基本原子构成,也称为字典。在信号中可以是不同频率的波形,在图像中可以是构成图像的基本边,角。
X可以由D中和少量原子线性组合而成,及其表示系数为稀疏。如下:
(2)数学模型
引出稀疏表示的两个基本要求
1:尽可能与原特征相似
2 : 系数为稀疏。
有上图中,我们要求p>m,根据线性代数的知识我们知道,稀疏系数有无穷多组的解。根据稀疏的条件,我们可以在所有的可行解中挑出非零元素最少的解,也就是满足稀疏性。于是得到如下的数学模型:
如果再考虑噪声的话,就得到如下的模型:
目标函数中为L0范数约束,是非确定性多项式(NP)难题,即是指可以在多项式时间内被非确定机(他可以猜,他总是能猜到最能满足你需要的那种选择,如果你让他解决n皇后问题,他只要猜n次就能完成----每次都是那么幸运)解决的问题.
有人做了一个证明,在一定条件下,上述的最优化问题有唯一的解。
Terry tao又证明了,在满足一定条件下,零范数问题与一范数问题是等价的。于是上述模型转化为:
一 Sparse Coding的基本原理
1.1 基本概念
稀疏编码最早由 Olshausen 和 Field 于 1996 年提出,用于解释大脑中的初期视觉处理(比如边缘检测)。
目标:给定一组输入数据向量 { x1,x2,...,xN },去学习一组基字典(dictionary of bases);
稀疏编码的目的:在大量的数据集中,选取很小部分作为元素来重建新的数据。
稀疏编码难点:其最优化目标函数的求解。
稀疏编码算法是一种无监督学习方法,它用于寻找一组“超完备基(over-complete bases)”来更高效地表示样本数据。换句话说,稀疏编码算法的目的就是找到一组基向量ϕ,使得我们能将输入向量 x 表示为这些基向量的线性组合:
其中 ai 的值大部分都为 0,所以称为「稀疏」。每一个数据向量都由稀疏线性权值与基的组合形式来表达。
虽然形如主成分分析技术(PCA)能使我们方便地找到一组“完备基向量(a complete set of basis vectors)”,但是这里我们想要的是找到一组“超完备基向量(an over-complete set of basis vectors)”来表示输入向量。也就是说基向量的数量要大于输入向量的维度。
超完备基的好处是它们能更有效地找出隐含在输入数据内部的结构与模式。然而,对于超完备基来说,系数 ai 不再由输入向量唯一确定。因此,在稀疏编码算法中,需要另加了一个评判标准“稀疏性(sparsity )”来解决因超完备(over-completeness)而导致的退化(degeneracy)问题。
1.2 完备基与超完备基
回顾一下PCA中如何计算一组完备基向量:
1)计算协方差矩阵
2)奇异值分解(Singular Value Decomposition)
3)降维or白化
这里第二步中得到的U就是所求的完备基(complete bases)。
那么什么是超完备基?其实就是在U中再多几列,例如:
为什么说:对于超完备基来说,系数 ai 不再由输入向量唯一确定?
根据basis的原理,训练集中任意一个向量都可以唯一表示为完备基向量的线性组合:
即系数a向量是唯一的,但对于超完备基来说,系数向量a就不唯一了,这也很好理解,毕竟超完备基中的基向量之间是线性相关的(任意n+1个n维向量必线性相关)。其实就类似于解方程组,k是变量数量,n是方程数量,如果方程较多而变量较少,则解是唯一的,如果方程较少而变量较多,则解是不唯一的。
因为稀疏编码目的是找到一组超完备基,即 k>n,所以就无法直接通过原始数据得到特征矩阵 U(一组完备基向量),进而也就无法直接得到系数 a,所以我们需要用学习的方式来找到这一组超完备基。
1.3 稀疏性(Sparsity)
这里把“稀疏性(sparsity )”定义为:只有很少的几个非零元素或只有很少的几个远大于零的元素。
要求系数向量 a 是稀疏的意思就是说:对于一个输入向量的基向量组合,我们只想有尽可能少的几个系数远大于零。
选择使用具有稀疏性的分量来表示我们的输入数据是有原因的,因为绝大多数的感官数据(sensory data),比如自然图像,可以被表示成少量基本元素(atomic elements)的叠加,在图像中这些基本元素可以是面或者线。同时,比如与初级视觉皮层的类比过程也因此得到了提升。
1.4 稀疏编码的相关解释
![]()
-
a 是稀疏,且超完备(over-complete)的表征;
-
编码函数 a = f(x) 是 x 的隐函数和非线性函数;
-
而重构(解码)函数 x' = g(a) 是线性且显性的。
关于稀疏性的讨论,可以参考:[机器学习] UFLDL笔记 - Autoencoders and Sparsity
二 Sparse Coding的训练与应用
2.1 代价函数
稀疏编码的代价函数定义如下:
- 第一项可解释为一个“重构项(reconstruction term)”,这一项迫使稀疏编码算法为输入向量提供一个高拟合度的线性表达式;
- 第二项即“稀疏惩罚项(sparsity penalty term)”,它使输入向量的表达式变得“稀疏”,也就是系数向量a变得稀疏。常量 λ 是一个变换量,由它来控制这两项式子的相对重要性。
虽然“稀疏性”的最直接度量标准是 “L0” 范式:
![]()
但这是不可微的,而且通常很难进行优化。在实际中,稀疏代价项 S(.) 的普遍选择是L1 范式代价函数(L1正则化):
![]()
或者对数形式:
![]()
同时,为了防止ai值过小的问题,我们对Φ的取值也进行了限制:
2.2 如何利用Sparse Coding提取数据特征?
简单来说,Sparse Coding是将输入数据重构为一组超完备基向量的线性组合,然后这些基向量前面的系数所构成的向量就是输入数据的新特征。
一般情况下要求超完备基向量的个数k非常大(远大于输入数据的维度n),因为这样的基向量组合才能更容易的学到输入数据内在的结构和特征。其实在常见的PCA算法中,是可以找到一组基来分输入数据X的,只不过那个基的数目比较小(小于等于输入数据维度),所以可以得到分解后的系数a是可以唯一确定,而在sparse coding中,k太大,比n大很多,其分解系数a不能唯一确定。
另外,Sparse Coding在实际使用过程中速度很慢,这是因为即使我们在训练阶段已经把输入数据集的超完备基学习到了,在测试阶段时还是要通过凸优化的方法去求得其特征值(即基组合前面的系数值),所以这比一般的前向神经网络速度要慢。
2.3 训练(train)
稀疏编码算法涉及超完备基Φ(字典)和系数向量a的学习,因此训练是由两个独立的优化过程组合起来的。每次迭代分两步:第一个是固定字典Φ,逐个使用训练样本x来优化系数 ai ,第二个是固定系数向量a,一次性处理多个样本对字典Φ进行优化。不断迭代,直至收敛,这就可以得到一组能够良好表示训练样本x的超完备基,也就是字典。
- 关于系数向量a的优化:
(1) 使用 L1 范式作为稀疏惩罚函数,对 a(j)i的学习过程就简化为求解“由 L1 范式正则化的最小二乘法问题”,这个问题函数在域 a(j)i内为凸,已经有很多技术方法来解决这个问题。
(2) 使用对数形式的稀疏惩罚函数,则可以采用基于梯度算法的方法,如共轭梯度法。
- 关于字典Φ的优化:
使用 L2 范式约束来学习基向量,同样可以简化为一个带有二次约束的最小二乘问题,其问题函数在域 Φ 内也为凸。
2.4 表示(representation)
根据前面的的描述,稀疏编码是有一个明显的局限性的,这就是即使已经学习得到一组基向量,如果为了对新的数据样本进行“编码”,我们必须再次执行优化过程来得到所需的系数a。这意味着在测试中,实现稀疏编码需要高昂的计算成本,尤其是与典型的前馈结构算法相比,例如稀疏自编码器。
稀疏编码用于表示的形象描述如下:
![]()
0, 0, ..., 0.8, ..., 0.3 ..., 0.5, ...] 为系数矩阵,也叫做特征表示(feature representation)。
下图为应用稀疏编码进行图像分类的相关实验结果,该实验是在 Caltech101 物体类别数据集中完成的,并且用经典的 SVM 作为分类算法。
![]()
三 Sparse Coding的Autoencoder Interpretation
3.1 Sparse Autoencoder VS Sparse Coding
在Sparse Autoencoder中,我们试着学习得到一组权重参数 W (以及相应的截距 b ),通过这组参数W可以得到输入样本的稀疏特征向量,也就是隐层的激励值向量,由此也就得到了输入样本的稀疏表示;
在Sparse Coding中,我们试图直接学习数据的稀疏特征向量,以及与之对应的超完备基(字典)。其实Sparse Coding的学习也是一种特征映射,目标是将原始训练样本映射成(重构为)稀疏表示形式。
UFLDL中说“稀疏编码可以看作是稀疏自编码方法的一个变形”。确切地说,在稀疏编码算法中,我们直接利用样本数据 x 进行特征学习,学习一个用于表示样本数据的稀疏特征 s(对应前面说的向量a),和一个将特征s从特征空间转换到样本数据空间的基底 A(对应前面说的超完备基Φ)。
3.2 Sparse Coding的代价函数重定义
基于上面的理解,我们重定义Sparse Coding的代价函数如下:
- 第一项是重构代价项(reconstruction cost term);
- 第二项是稀疏惩罚项(sparsity penalty term);
- 第三项是权重衰减项(weight decay term)。
具体对每一项的构建原因和解释可以查看UFLDL的教程,讲解的很清楚。
3.3 重构项的理解
为了理解重构代价项,我们将该代价函数与PCA进行对比。
矩阵 A 是一组超完备基向量组成的,每一列是一个基向量,向量 s 是稀疏特征向量。这里其实跟PCA中数据近似还原计算的非常类似,PCA的数据近似还原计算如下:
Sparse Coding中的A就对应PCA中的U,s对应x_rot。只不过,Sparse Coding目的是找到一组“超完备基向量”,PCA目的是找到一组“完备基向量”。
注意,在UFLDL教程中代价函数的重构代价项没有*(1/m),这是不对的。重构代价项实际上是均方误差,而不是误差平方和。
参考:http://ufldl.stanford.edu/wiki/index.php/Sparse_Coding:_Autoencoder_Interpretation
3.3 权重衰减项的意义
如果只有前面两项(重构代价项和稀疏惩罚项),那么就存在一个问题: 如果将系数向量s中各项系数值减到很小,且将字典A中每个基向量的值增加到很大,这样第一项的代价值基本保持不变,而第二项的稀疏惩罚值却会相应变小。也就是说只要将所有系数都减小同时基向量的值增大,那么就能最小化上面的代价函数。在这种情况下,所有的系数a都变得很小,即:它们都大于0但接近于0,而这并不满足我们对系数向量的稀疏性要求:系数向量s中只有少数系数远远大于0,而不是大部分系数都接近于0。
所以为了防止这种情况发生,我们需要保证字典A中基向量的元素值都不会变得太大,这就是权重衰减项的意义。
3.5 Sparse Coding的迭代优化过程
1. 随机初始化A
2. 重复以下步骤直至收敛:
a. 根据上一步给定的A,求解能够最小化J(A,s)的s
b. 根据上一步得到的s,求解能够最小化J(A,s)的A
理论上,Sparse Coding通过上述迭代方法求解目标函数的最优化问题最终得到的稀疏特征向量与通过Sparse Autoencoder学习得到的稀疏特征向量是差不多的。
四 Topographic Sparse Coding
4.1 基本概念
首先看一下大脑皮层中的特征秩序,摘录自UFLDL-Topographic Sparse Coding。 举个例子,视觉特征,如前面所提到的,大脑皮层 V1 区神经元能够按特定的方向对边缘进行检测,同时,这些神经元(在生理上)被组织成超柱(hypercolumns),在超柱中,相邻神经元以相似的方向对边缘进行检测,一个神经元检测水平边缘,其相邻神经元检测到的边缘就稍微偏离水平方向,沿着超柱,神经元就可以检测到与水平方向相差更大的边缘了。
受该例子的启发,我们希望学习到的特征也具有这样“拓扑秩序(topographically ordered)”的性质。这对于我们要学习的特征意味着什么呢?直观的讲,如果“相邻”的特征是“相似”的,就意味着如果某个特征被激活,那么与之相邻的特征也将随之被激活。
通过Sparse Coding已经可以得到样本数据的稀疏表示。进一步,我们通过分组的方式,来使得学习得到的特征集中各项之间具有某种“秩序(orderly)”。
4.2 代价函数
具体而言,假设我们将特征组织成一个方阵。我们就希望矩阵中相邻的特征(adjacent features)是相似的。实现这一点的方法是将相邻特征按“经过平滑的L1范式惩罚(the smoothed L1 penalty)” 进行分组,如果按 3x3 方阵分组,则是用:
![]()
代替:
![]()
其分组通常是重合的,例如从第 1 行第 1 列开始的 3x3 区域是一个分组,从第 1 行第 2 列开始的 3x3 区域是另一个分组,以此类推。最终,这样的分组会形成环绕,就好像这个矩阵是个环形曲面,所以每个特征都以同样的次数进行了分组。也就是说,将经过平滑的所有分组的 L1 惩罚值之和代替经过平滑的 L1 惩罚值,得到新的代价函数:
进一步,我们将分组的操作通过“分组矩阵V”来完成,分组矩阵 V 的第 r 行标识了哪些特征被分到第 r 组中,即如果第 r 组包含特征 c ,则 Vr,c = 1,示例如下:
通过分组矩阵实现分组使得目标函数的梯度计算更加直观,使用此分组矩阵后目标函数被重写为:
该目标函数能够使用之前部分提到的迭代方法进行求解。拓扑稀疏编码得到的特征与稀疏编码得到的类似,只是拓扑稀疏编码得到的特征是以某种方式有“秩序”排列的。
关于分组后的稀疏惩罚项的对s的梯度推导过程,可以参考:[机器学习] UFLDL笔记 - 反向传播算法(Backpropagation)
五 Sparse Coding的训练注意事项
5.1 实验笔记
这部分是我在实现Sparse Coding时候的一些实验笔记。
1)优化算法对结果是有影响的。比如,对于拓扑稀疏编码,优化算法为cg,特征个数为121,小图像块大小为16*16时,cg算法得到的结果比lbfgs算法更好。
2)patch大小对结果是有影响的。比如,拓扑稀疏编码算法,特征个数为121,采样patch大小为8*8时,如果用lbfgs算法就得不到结果,而用cg算法就可以得到上面的结果。
3)规律:随着迭代次数的增加,代价函数值应该是越来越小的,如果不是,就永远不会得到正确结果。如果代价函数不是越来越小,可能是优化算法的选择有问题,或者小图像块的选择有问题,具体情况具体分析,有多种原因。当然更本质的原因,还没弄清楚。
4)训练集中的10张512*512的灰度图像是已经白化后的图像,故它的值不是在[0,1]之间。以前实验的sampleIMAGES函数中要把样本归一化到[0,1]之间的原因在于它们都是输入到稀疏自动编码器,其要求输入数据为[0,1]范围,而本节实验是把数据输入到稀疏编码中,它并不要求数据输入范围为[0,1],同时归一化本身实际上是有误差的(因为它是根据3sigma法则归一化的),所以本节实验修改后的sampleIMAGES函数中,不需要再把随机抽取20000张小图像块归一化到[0,1]范围,即:要把原来sampleIMAGES函数中如下代码注释掉:patches = normalizeData(patches);。实际上这一步非常重要,因为它直接关系到最后是否可以得到要求的结果图。
5.2 实验效果
topographic的实验结果如下:
topographic:迭代200次,patchDim = 16; Method = ‘cg’;
所谓“ordered”,一眼就可以看出来了吧。
基础补充
L0范数与L1范数
L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0,换句话说,让参数W是稀疏的。OK,看到了“稀疏”二字,大家应该意识到,原来用的漫山遍野的“稀疏”就是通过这玩意来实现的。但是看到的papers世界中,稀疏不是都通过L1范数来实现吗?这个时候你又该怀疑了,脑海里是不是到处都是||W||1影子呀!
L1范数是指向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)。现在我们来分析下这个价值一个亿的问题:为什么L1范数会使权值稀疏?有人可能会这样给你回答“它是L0范数的最优凸近似”。实际上,还存在一个更美的回答:任何的规则化算子,如果他在Wi=0的地方不可微,并且可以分解为一个“求和”的形式,那么这个规则化算子就可以实现稀疏。这说是这么说,W的L1范数是绝对值,|w|在w=0处是不可微,但这还是不够直观。这里因为我们需要和L2范数进行对比分析。所以关于L1范数 的直观理解,请待会看看第二节。
那么还有一个问题:既然L0可以实现稀疏,为什么不用L0,而要用L1呢?本人查资料理解为两点:
1.因为L0范数很难优化求解(NP难问题)
2.L1范数是L0范数的最优凸近似,而且它比L0范数要容易优化求解。所以大家才把目光和万千宠爱转于L1范数。
![]()
小结:L1范数和L0范数可以实现稀疏,L1因具有比L0更好的优化求解特性而被广泛应用。
为什么要稀疏?让我们的参数稀疏有什么好处呢?:
1)特征选择(Feature Selection):
原始的模式识别是直接对原始图形进行特征提取,而所提取出来的特征和最终的输出很多情况下其实是有冗余成分的,就是说我们只需要关键特征识别就可以,没有必要用那么多特征,更多情况下,那些冗余信息会干扰我们最后的识别结果!
稀疏编码算法是一种无监督学习方法,它用来寻找一组“超完备”基向量来更高效地表示样本数据。大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说,xi的大部分元素(也就是特征)都是和最终的输出yi没有关系或者不提供任何信息的,在最小化目标函数的时候考虑xi这些额外的特征,虽然可以获得更小的训练误差,但在预测新的样本时,这些没用的信息反而会被考虑,从而干扰了对正确yi的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。
2)可解释性(Interpretability):
另一个青睐于稀疏的理由是,模型更容易解释。例如患某种病的概率是y,然后我们收集到的数据x是1000维的,也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型:y=w1*x1+w2*x2+…+w1000*x1000+b(当然了,为了让y限定在[0,1]的范围,一般还得加个Logistic函数)。
说简单些,logistic函数其实就是这样一个函数:
![]()
这个函数的曲线如下所示:
![]()
很像一个“S”型吧,所以又叫 sigmoid曲线(S型曲线)。
通过学习,如果最后学习到的w*就只有很少的非零元素,例如只有5个非零的wi,那么我们就有理由相信,这些对应的特征在患病分析上面提供的信息是巨大的,决策性的。也就是说,患不患这种病只和这5个因素有关,那医生就好分析多了。但如果1000个wi都非0,医生面对这1000种因素,累觉不爱。
L2范数
L2范数: ||W||2,在回归里面,有人把有它的回归叫“岭回归”(Ridge Regression),有人也叫它“权值衰减weight decay”。它的强大功效是改善机器学习里面一个非常重要的问题:过拟合。就是模型训练时候的误差很小,但在测试的时候误差很大,也就是我们的模型复杂到可以拟合到我们的所有训练样本了,但在实际预测新的样本的时候,糟糕的一塌糊涂。例如下图所示(来自Ng的course):
![]()
上面的图是线性回归,下面的图是Logistic回归,也可以说是分类的情况。从左到右分别是欠拟合(underfitting,也称High-bias)、合适的拟合和过拟合(overfitting,也称High variance)三种情况。可以看到,如果模型复杂(可以拟合任意的复杂函数),它可以让我们的模型拟合所有的数据点,也就是基本上没有误差。对于回归来说,就是我们的函数曲线通过了所有的数据点,如上图右。对分类来说,就是我们的函数曲线要把所有的数据点都分类正确,如下图右。这两种情况很明显过拟合了。
![]()
L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项||W||2最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0,这里是有很大的区别的哦。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。我的理解是:限制了参数很小,实际上就限制了多项式某些分量的影响很小(看上面线性回归的模型的那个拟合的图),这样就相当于减少参数个数。其实我也不太懂,希望大家可以指点下。
这里也一句话总结下:通过L2范数,我们可以实现了对模型空间的限制,从而在一定程度上避免了过拟合。
L2范数的好处是什么呢?
1)学习理论的角度: 从学习理论的角度来说,L2范数可以防止过拟合,提升模型的泛化能力。
2)优化计算的角度:
从优化或者数值计算的角度来说,L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。哎,等等,这condition number是啥?我先google一下哈。
优化有两大难题
- 一是:局部最小值:我们要找的是全局最小值,如果局部最小值太多,那我们的优化算法就很容易陷入局部最小
- 二是:ill-condition病态问题。。假设我们有个方程组AX=b,我们需要求解X。如果A或者b稍微的改变,会使得X的解发生很大的改变,那么这个方程组系统就是ill-condition的,反之就是well-condition的。举例:
![]()
咱们先看左边的那个。第一行假设是我们的AX=b,第二行我们稍微改变下b,得到的x和没改变前的差别很大,看到吧。第三行我们稍微改变下系数矩阵A,可以看到结果的变化也很大。换句话来说,这个系统的解对系数矩阵A或者b太敏感了。又因为一般我们的系数矩阵A和b是从实验数据里面估计得到的,所以它是存在误差的,如果我们的系统对这个误差是可以容忍的就还好,但系统对这个误差太敏感了,以至于我们的解的误差更大,那这个解就太不靠谱了。所以这个方程组系统就是ill-conditioned病态的,不正常的,不稳定的,有问题的,哈哈。这清楚了吧。右边那个就叫well-condition的系统了。
condition number就是拿来衡量ill-condition系统的可信度的。condition number衡量的是输入发生微小变化的时候,输出会发生多大的变化。也就是系统对微小变化的敏感度。condition number值小的就是well-conditioned的,大的就是ill-conditioned的。
也就是矩阵A的norm乘以它的逆的norm。如果方阵A是奇异的,那么A的condition number就是正无穷大了。实际上,每一个可逆方阵都存在一个condition number。但如果要计算它,我们需要先知道这个方阵的norm(范数)和Machine Epsilon(机器的精度)。为什么要范数?范数就相当于衡量一个矩阵的大小,我们知道矩阵是没有大小的,当上面不是要衡量一个矩阵A或者向量b变化的时候,我们的解x变化的大小吗?所以肯定得要有一个东西来度量矩阵和向量的大小吧?对了,他就是范数,表示矩阵大小或者向量长度。OK,经过比较简单的证明,对于AX=b,我们可以得到以下的结论:
![]()
也就是我们的解x的相对变化和A或者b的相对变化是有像上面那样的关系的,其中k(A)的值就相当于倍率,看到了吗?相当于x变化的界。
对condition number来个一句话总结:condition number是一个矩阵(或者它所描述的线性系统)的稳定性或者敏感度的度量,如果一个矩阵的condition number在1附近,那么它就是well-conditioned的,如果远大于1,那么它就是ill-conditioned的,如果一个系统是ill-conditioned的,它的输出结果就不要太相信了。
从优化或者数值计算的角度来说,L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。因为目标函数如果是二次的,对于线性回归来说,那实际上是有解析解的,求导并令导数等于零即可得到最优解为:
![]()
然而,如果当我们的样本X的数目比每个样本的维度还要小的时候,矩阵XTX将会不是满秩的,也就是XTX会变得不可逆,所以w*就没办法直接计算出来了。或者更确切地说,将会有无穷多个解(因为我们方程组的个数小于未知数的个数,也就是说压缩感知机中的Y=DX,起初构造的测量矩阵就是这样的M*N(M 但如果加上L2规则项,就变成了下面这种情况,就可以直接求逆了: 这里面,专业点的描述是:要得到这个解,我们通常并不直接求矩阵的逆,而是通过解线性方程组的方式(例如高斯消元法)来计算。考虑没有规则项的时候,也就是λ=0的情况,如果矩阵XTX的 condition number 很大的话,解线性方程组就会在数值上相当不稳定,而这个规则项的引入则可以改善condition number。 另外,如果使用迭代优化的算法,condition number 太大仍然会导致问题:它会拖慢迭代的收敛速度,而规则项从优化的角度来看,实际上是将目标函数变成λ-strongly convex(λ强凸)的了。哎哟哟,这里又出现个λ强凸,啥叫λ强凸呢? 当f满足时,我们称f为λ-stronglyconvex函数,其中参数λ>0。当λ=0时退回到普通convex 函数的定义。 在直观的说明强凸之前,我们先看看普通的凸是怎样的。假设我们让f在x的地方做一阶泰勒近似(一阶泰勒展开忘了吗?f(x)=f(a)+f'(a)(x-a)+o(||x-a||).): 直观来讲,convex 性质是指函数曲线位于该点处的切线,也就是线性近似之上,而 strongly convex 则进一步要求位于该处的一个二次函数上方,也就是说要求函数不要太“平坦”而是可以保证有一定的“向上弯曲”的趋势。专业点说,就是convex 可以保证函数在任意一点都处于它的一阶泰勒函数之上,而strongly convex可以保证函数在任意一点都存在一个非常漂亮的二次下界quadratic lower bound。当然这是一个很强的假设,但是同时也是非常重要的假设。可能还不好理解,那我们画个图来形象的理解下。 我们取我们的最优解w*的地方。如果我们的函数f(w),见左图,也就是红色那个函数,都会位于蓝色虚线的那根二次函数之上,这样就算wt和w*离的比较近的时候,f(wt)和f(w*)的值差别还是挺大的,也就是会保证在我们的最优解w*附近的时候,还存在较大的梯度值,这样我们才可以在比较少的迭代次数内达到w*。但对于右图,红色的函数f(w)只约束在一个线性的蓝色虚线之上,假设是如右图的很不幸的情况(非常平坦),那在wt还离我们的最优点w*很远的时候,我们的近似梯度(f(wt)-f(w*))/(wt-w*)就已经非常小了,在wt处的近似梯度∂f/∂w就更小了,这样通过梯度下降wt+1=wt-α*(∂f/∂w),我们得到的结果就是w的变化非常缓慢,像蜗牛一样,非常缓慢的向我们的最优点w*爬动,那在有限的迭代时间内,它离我们的最优点还是很远。 所以仅仅靠convex 性质并不能保证在梯度下降和有限的迭代次数的情况下得到的点w会是一个比较好的全局最小点w*的近似点(插个话,有地方说,实际上让迭代在接近最优的地方停止,也是一种规则化或者提高泛化性能的方法)。正如上面分析的那样,如果f(w)在全局最小点w*周围是非常平坦的情况的话,我们有可能会找到一个很远的点。但如果我们有“强凸”的话,就能对情况做一些控制,我们就可以得到一个更好的近似解。至于有多好嘛,这里面有一个bound,这个 bound 的好坏也要取决于strongly convex性质中的常数α的大小。看到这里,不知道大家学聪明了没有。如果要获得strongly convex怎么做?最简单的就是往里面加入一项(α/2)*||w||2。 呃,讲个strongly convex花了那么多的篇幅。实际上,在梯度下降中,目标函数收敛速率的上界实际上是和矩阵XTX的 condition number有关,XTX的 condition number 越小,上界就越小,也就是收敛速度会越快。 总结:L2范数不但可以防止过拟合,还可以让我们的优化求解变得稳定和快速。 1)下降速度: 我们知道,L1和L2都是规则化的方式,我们将权值参数以L1或者L2的方式放到代价函数里面去。然后模型就会尝试去最小化这些权值参数。而这个最小化就像一个下坡的过程,L1和L2的差别就在于这个“坡”不同,如下图:L1就是按绝对值函数的“坡”下降的,而L2是按二次函数的“坡”下降。所以实际上在0附近,L1的下降速度比L2的下降速度要快。所以会非常快得降到0。不过我觉得这里解释的不太中肯,当然了也不知道是不是自己理解的问题。 L1在江湖上人称Lasso,L2人称Ridge。不过这两个名字还挺让人迷糊的,看上面的图片,Lasso的图看起来就像ridge,而ridge的图看起来就像lasso。 2)模型空间的限制: 实际上,对于L1和L2规则化的代价函数来说,我们可以写成以下形式: 也就是说,我们将模型空间限制在w的一个L1-ball 中。为了便于可视化,我们考虑两维的情况,在(w1, w2)平面上可以画出目标函数的等高线,而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解: 可以看到,L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现,而目标函数的测地线除非位置摆得非常好,大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性,例如图中的相交点就有w1=0,而更高维的时候(想象一下三维的L1-ball 是什么样的?)除了角点以外,还有很多边的轮廓也是既有很大的概率成为第一次相交的地方,又会产生稀疏性。 相比之下,L2-ball 就没有这样的性质,因为没有角,所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性,而L2-regularization 不行的原因了。 因此,一句话总结就是:L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已![]()
![]()
![]()
![]()
L1和L2的差别:为什么一个让绝对值最小,一个让平方最小,会有那么大的差别呢?我看到的有两种几何上直观的解析:
![]()
![]()
![]()
参考资料