K-means算法理论+代码实现
- K-means算法理论
- 代码实现
- K值选择
- 聚类过程
K-means理论
首先,这里我们用sklearn库中datasets里的make_blobs函数产生数据
make_blobs函数:生成各向同性高斯blob用于聚类
#聚类算法 K-means,划分聚类方法
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt
import time
time1 = time.clock()
#data,label = sklearn.datasets.make_blobs(n_samples = 100,n_features = 2,centers = 3,center_box = (-10.0,10.0),random_state = None)
#n_sample是生成的数据总个数,n_features是指每个样本的特征个数,centers指的是中心点的数目,centers_boxs指的是范围,random_state指的是随机数种子
#make_blobs生成特定的团状数据
#构造数据
blobs, _ = make_blobs(n_samples=200, centers=3, random_state=18)#center用来控制堆数
#print(blobs[:10]) # 打印出前 10 条数据的信息
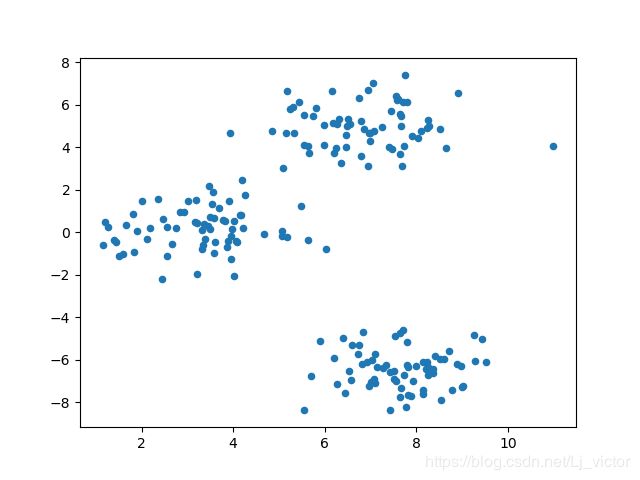
#数据可视化(画出make_blobs函数产生的样本)
plt.scatter(blobs[:,0],blobs[:,1],s=20)
plt.show()
def random_k(k,data):
prng = np.random.RandomState(27)#定义随机数种子
num_feature = np.shape(data)[1]#特征数,在data里位于1的位置
init_centers = prng.randn(k,num_feature)*5#乘以5是优化的地方,更接近样本值
#生成k*feature的随机数,k个样本,每个样本内有feature个特征
return init_centers
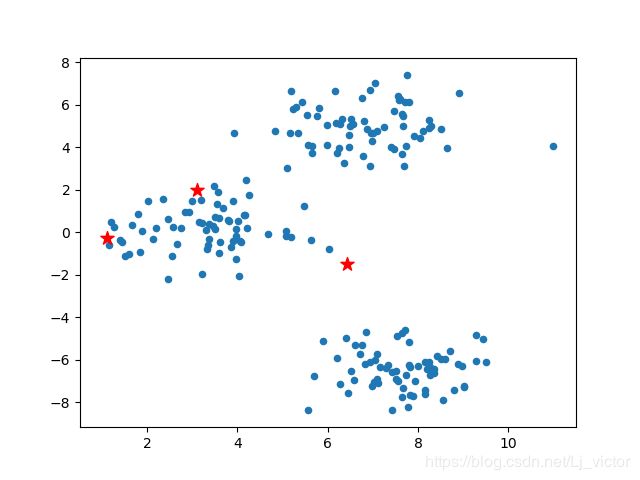
init_centers = random_k(3,blobs)
plt.scatter(blobs[:, 0], blobs[:, 1], s=20)
plt.scatter(init_centers[:,0], init_centers[:,1], s=100, marker='*', c="r")
plt.show()
计算欧氏距离
def d_euc(x,y):#x,y指的是不同的样本
d = np.sqrt(np.sum(np.square(x - y)))
return d
更新中心点
def update_center(clusters,data,centers):
#clusters:每一点分好的类别 centers:中心点集合 ; 返回值→新中心点集合:new_center.reshape(num_centers,num_features)
num_centers = np.shape(centers)[0] #中心点的个数
num_features = np.shape(centers)[1]#特征数
containers = []
for x in range(num_centers):
each_container = []
containers.append(each_container)#container是总的容器,each_container是指每个容器,目前都是空的
for i,cluster in enumerate(clusters):#enumerate函数,可以用作标号,cluster是标号(这里指每个样本的类别)
containers[cluster].append(data[i])
#为方便计算,list类型转换为np.array类型
containers = np.array(list(map(lambda x:np.array(x),containers)))
new_centers = np.array([])#存放中心点的坐标
for i in range(len(containers)):
each_center = np.mean(containers[i],axis=0)#计算每一个类的均值中心为新的中心点
new_centers = np.append(new_centers,each_center)
return new_centers.reshape(num_centers, num_features)
K-means核心代码
这里精简算法的步骤是difference[],无需重复迭代
def kmeans(data,init_centers,k):
max_step = 50 #定义迭代次数
epsilon = 0.001 #定义足够小的数来判断中心点位置是否变化
old_centers = init_centers
centers_container = [] #建立一个中心点容器,存放每一次变化后的中心点,以便后面的绘图
cluster_container = []
centers_container.append(old_centers)
for step in range(max_step):#每一次迭代
clusters = np.array([],dtype=int)#每一个样本点归的类
for each_data in data:
distances = np.array([])
for each_center in old_centers:#中心点数目
temp_distance = d_euc(each_data,each_center)#样本到该中心点的欧式距离
distances = np.append(distances,temp_distance)
lab = np.argmin(distances)#判断距离each_data最近的中心点#???牵引回来的是什么
clusters = np.append(clusters,lab)#
cluster_container.append(clusters)
new_centers = update_center(clusters,data,old_centers)
#减少多余迭代,如果都不需要更新了就不需要再迭代了,减少时间
difference = []
for each_old_center,each_new_center in zip(old_centers,new_centers):
difference.append(d_euc(each_old_center,each_new_center))
if(np.array(difference) < epsilon).all():
return centers_container, cluster_container
centers_container.append(new_centers)
old_centers = new_centers
return centers_container, cluster_container
"""计算最终中心点
"""
centers_container, cluster_container = kmeans(blobs, init_centers, 3)
final_center = centers_container[-1]
final_cluster = cluster_container[-1]
print(final_center)
time2 = time.clock()
diff_time = time2 - time1
print(diff_time)
"""可视化展示
"""
plt.scatter(blobs[:, 0], blobs[:, 1], s=20, c=final_cluster);
plt.scatter(final_center[:,0], final_center[:,1], s=100, marker='*', c="r")
#plt.show()
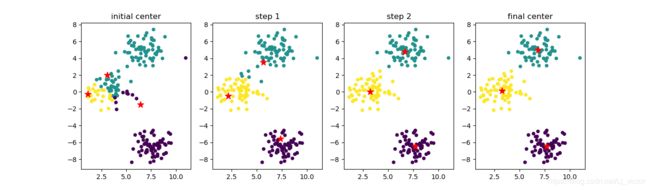
#中心点移动过程
num_axes = len(centers_container)
fig, axes = plt.subplots(1, num_axes, figsize=(20, 4))
axes[0].scatter(blobs[:, 0], blobs[:, 1], s=20, c=cluster_container[0])
axes[0].scatter(init_centers[:, 0], init_centers[:, 1], s=100, marker='*', c="r")
axes[0].set_title("initial center")
for i in range(1, num_axes-1):
axes[i].scatter(blobs[:, 0], blobs[:, 1], s=20, c=cluster_container[i])
axes[i].scatter(centers_container[i][:, 0],
centers_container[i][:, 1], s=100, marker='*', c="r")
axes[i].set_title("step {}".format(i))
axes[-1].scatter(blobs[:, 0], blobs[:, 1], s=20, c=cluster_container[-1])
axes[-1].scatter(final_center[:, 0], final_center[:, 1], s=100, marker='*', c="r")
axes[-1].set_title("final center")
plt.show()
迭代过程:
这里我们发现,迭代4次就结束了,如果不用difference[]的话,就会一直迭代,浪费时间
(因为数据是利用make_blobs()函数创造的,所以迭代次数少)
初始化中心点的位置很好,比较均匀分布在了数据范围中。如果初始化中心点集中分布在某一角落,迭代次数肯定会增加。
示例数据分布规整和简单,使得无需迭代多次就能收敛