广度和深度优先搜索
搜索是树或者图等数据结构的基础算法之一,很多时候我们需要在树或者图中寻找特定的节点,那么使用到的最基础的、也是最容易理解的两种方式便是广度和深度优先搜索。
在开始阅读之前,做为预备知识,你可以先了解一下关于树和图这两种数据结构的基本概念,参考 Wikipedia 上面的介绍:
Wikipedia——树(数据结构)
Wikipedia——图(数据结构)
以及其他一些优秀的文章:
https://segmentfault.com/a/1190000010794621
https://www.cnblogs.com/maybe2030/p/4732377.html
https://www.tutorialspoint.com/data_structures_algorithms/tree_data_structure.htm
https://www.geeksforgeeks.org/graph-data-structure-and-algorithms/
一、广度优先搜索
1.1 基本概念
广度优先搜索(Breadth First Search),即 BFS,它是一种暴力搜索算法,采用地毯式层层推进的搜索方式,它从特定的节点开始,每一次都遍历离自己最近的节点,然后再依次向外遍历,直到找到需要的节点,或者全部遍历完毕,每个节点仅遍历一次。
1.2 作用于树
作用于树的话,广度优先搜索理解起来比较的直观,首先从根节点开始,然后再一层一层的往下遍历,你可以从下面的图中理解搜索的顺序(这里我以最常见的二叉树为例,其实作用于任何形式的树都是类似的,图中的虚线为搜索的路径):
相信你已经发现了,其实在树上面的广度优先搜索,就是按层级遍历整个树。在代码实现上面,广度优先搜索使用了一个队列,队列是一个先进先出的数据结构,与广度优先搜索的遍历次序能够吻合。
具体的流程是这样的:首先根节点先入队列,然后每次从队列中取出一个节点,并将这个节点的所有子节点放入队列中,然后继续相同的操作,当队列为空时,整个遍历便完成了。你可以结合代码实现来理解一下:
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class BreadthFirstSearch:
# 广度优先搜索-树
def bfs_tree(self, root: TreeNode):
if not root:
return
que = [root]
res = []
while que:
node = que.pop(0)
res.append(node.val)
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
return res
1.3 作用于图
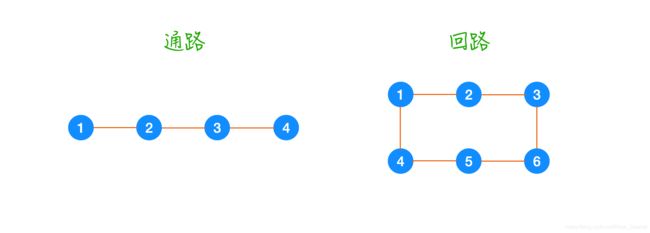
图是一种较为复杂的非线性数据结构,你可以将它理解为一种特殊的树,普通的树这种结构,是不存在回路的,也就是说它的节点都是连通的。这里涉及到了两个概念,分别是通路和回路,看下图的描述你就能够理解了:
因此图其实就是一种有回路的树,正因为这一点,在图上的广度优先搜索,必须判断节点是否已经遍历过,否则可能会出现重复遍历的情况,在代码实现上一般会采用一个 set 进行判重。下图展示了图上的广度优先搜索的过程:
下面是一个简单的代码实现:
# 定义图
class Graph:
def __init__(self, vertex: int):
self.vertex = vertex
self.adj = [[] for _ in range(vertex)]
def add_edge(self, s: int, t: int):
self.adj[s].append(t)
self.adj[t].append(s)
class BreadthFirstSearch:
# 广度优先搜索-图
def bfs_graph(self, graph: Graph, s: int):
if not graph:
return
visited, que, res = set(), [], []
visited.add(s)
que.append(s)
res.append(s)
while que:
p = que.pop(0)
for n in graph.adj[p]:
if n not in visited:
visited.add(n)
res.append(n)
que.append(n)
return res
1.5 六度分隔理论
下面列举一个关于广度优先的示例,帮助你加深理解。
在社交关系中,有一个很有趣的理论叫做六度分隔,它的意思是你与这个世界上任何一个人的距离不会超过 6 个人,哈佛大学一位心理学教授于 1967 年根据这个概念做过一次连锁实验,尝试证明平均只需要 6 步就可以联系任何两个互不相识的人。
我们可以这样理解:假如你所认识的人的总和为 100 个,其实你可以估算一下,认识 100 个人应该不算多。那么你认识的这 100 个人中,每个人各自又认识 100 个人,这样的话总和就是 1002,这就是二度好友关系,那么到第五度的时候,人数就有 100 亿了,已经超过了目前世界的人口总和,就算算上一些重复的好友关系,那么六度好友的总和也会远远超过全世界人口。
虽然这个理论目前存在很大的争议,但是它表达了一个很重要的概念:在任何两位素不相识的人之间,通过一定的联系方式,总能够产生必然联系或关系。
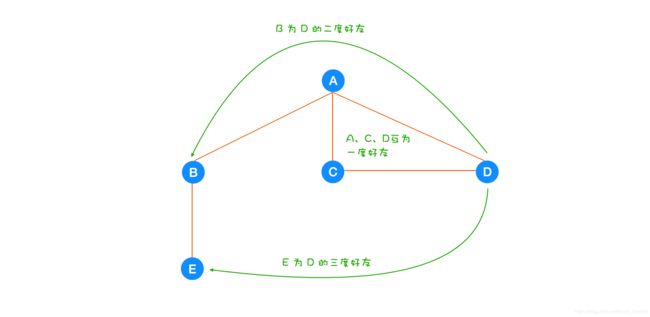
我们可以将人际关系使用一个图(数据结构)来表示,就像下面这样:
那应该怎么找到一个人的一度好友、二度好友、n 度好友呢?我们可以从一个节点出发,找到其所有的一度好友,然后以一度好友的节点为基础,向外扩散寻找其二度好友,直到全部遍历完毕。相信你已经发现了,这其实和广度优先搜索的思路是一样的,下面我结合代码来展示。
首先定义一个表示好友关系的 Node 类,不重复的 userId 标识每一个人,一个 set 存储其所有的好友,常量 degree 表示好友的度数。
private static class Node{
Integer userId;
Set<Integer> friends;
int degree;
public Node(Integer userId) {
this.userId = userId;
this.friends = new HashSet<>();
this.degree = 0;
}
}
然后随机生成好友之间的关系:
private static final int userNum = 10;
private static final int relationNum = 10;
public static void main(String[] args) {
//随机生成好友之间的关系
Node[] userNodes = new Node[userNum];
for (int i = 0; i < userNum; i++) {
userNodes[i] = new Node(i);
}
Random random = new Random();
for (int i = 0; i < relationNum; i++) {
int friendA = random.nextInt(userNum);
int friendB = random.nextInt(userNum);
if (friendA == friendB){
continue;
}
userNodes[friendA].friends.add(friendB);
userNodes[friendB].friends.add(friendA);
}
}
然后便使用广度优先搜索查找用户的所有好友:
public static void bfs(Node[] userNodes, Integer userId){
if (userId == null || userId >= userNum){
return;
}
Queue<Integer> queue = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
queue.add(userId);
visited.add(userId);
while (!queue.isEmpty()){
Integer cur = queue.poll();
if (userNodes[cur].friends.isEmpty()){
continue;
}
for (int friend : userNodes[cur].friends) {
//已访问过则跳过
if (visited.contains(friend) || userNodes[friend] == null) {
continue;
}
visited.add(friend);
queue.add(friend);
userNodes[friend].degree = userNodes[cur].degree + 1;
System.out.println(String.format("%d度好友:%d", userNodes[friend].degree, friend));
}
}
}
二、深度优先搜索
2.1 基本概念
前面的广度优先搜索其实理解起来并不难,因为它的搜索方式和人的思维方式是类似的,但是深度优先搜索就不一样了,它的搜索方式可能理解起来并不是非常的直观,它更加符合计算机的“思维方式”。深度优先搜索从一个节点开始,依次查找和这个节点连通的所有节点,然后再回退至起始节点,并且在回退的过程中,查看是否有遗漏的节点,并继续同样的操作。
2.2 作用于树
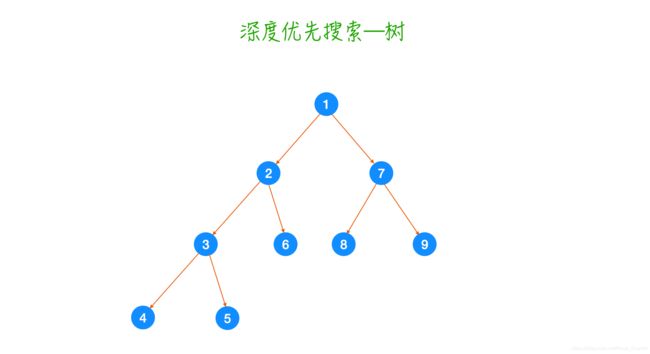
上面的概念解释你理解起来可能有点抽象,我画了一张在树上面的深度优先搜索的图片,你可以结合下图来理解(节点中的数字表示的是搜索的顺序):
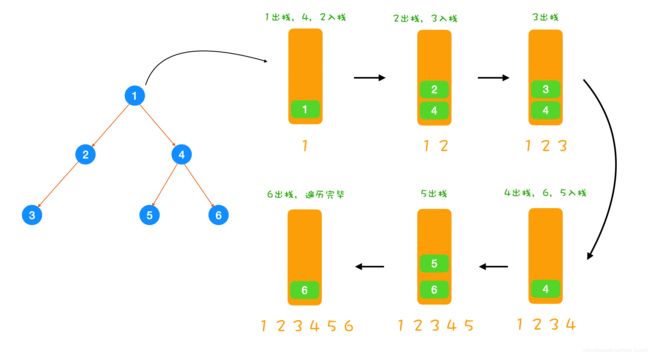
根据深度优先搜索的特性,我们可以借助一个栈来保存节点,栈是一种先进后出的数据结构,能够和搜索的访问顺序结合起来。首先是根节点先入栈,然后每次从栈中取出一个节点,并将其子节点全部压入栈中,然后再从栈中取出节点,循环这个过程,直到栈为空遍历完成。
你可以结合下面的图来理解整个过程:
在代码实现上面,你可以直接对照着上图的流程,使用一个栈来保存搜索的顺序,当然也可以使用递归的方式,这两者在本质上是没有区别的,下面是一个简单的代码示例:
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class DepthFirstSearch:
"""
深度优先搜索-树
"""
def __init__(self):
self.res = []
# 使用栈
def dfs_tree_stack(self, root: TreeNode):
if not root:
return
stack, res = [root], []
while stack:
node = stack.pop()
res.append(node.val)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return res
# 使用递归
def dfs_tree_recursive(self, root: TreeNode):
if not root:
return
self.res.append(root.val)
if root.left:
self.dfs_tree_recursive(root.left)
if root.right:
self.dfs_tree_recursive(root.right)
return self.res
2.3 作用于图
在图上面的深度优先搜索,由于节点可能存在回路,因此必须保存被访问过的节点用来判重,这和广度优先搜索是类似的。
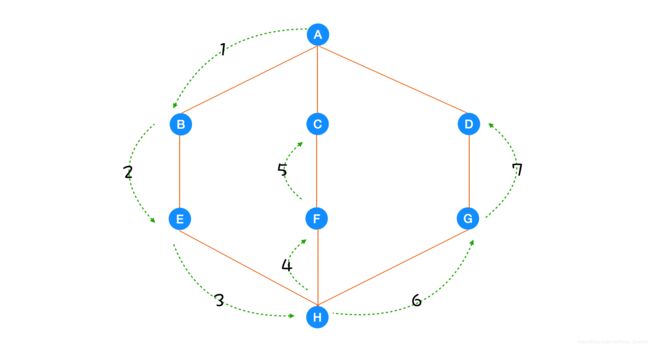
下图展示了在图上的深度优先搜索的路径(虚线上的数字表示访问的顺序):
下面是一个简单的代码示例:
class Graph:
def __init__(self, vertex: int):
self.vertex = vertex
self.adj = [[] for _ in range(vertex)]
def add_edge(self, s: int, t: int):
self.adj[s].append(t)
self.adj[t].append(s)
class DepthFirstSearch:
"""
深度优先搜索—图
"""
def __init__(self):
self.res = []
self.visited = set()
# 搜索一条s -> t的路径
def dfs_graph(self, graph: Graph, s: int, t: int):
if not graph:
return
self.res.append(s)
self.visited.add(s)
for n in graph.adj[s]:
if n not in self.visited:
if n == t:
self.res.append(n)
return self.res
self.dfs_graph(graph, n, t)
return self.res
注意这里我是使用的递归,你也可以使用栈来实现同样的逻辑。