数据结构篇——优先队列(堆)
目录
优先队列
二叉堆
堆定义:
堆操作
插入
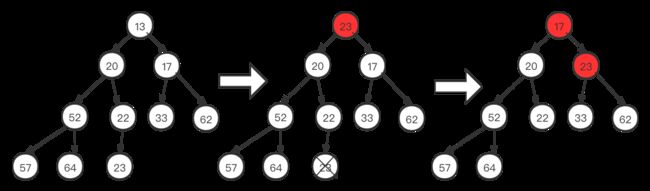
删除(最小元)
降低值
增加值
删除
构建堆(将一个无序的二叉树变为堆)
标准模板库的priority_queue
优先队列的构造
成员函数
用到优先队列的例题
UVA 11997
优先队列
优先队列也是一种队列,具有高级别元素先出队的特征。优先队列的工作是找出、返回、删除最高级别元素。优先队列的实现普遍用二叉堆
二叉堆
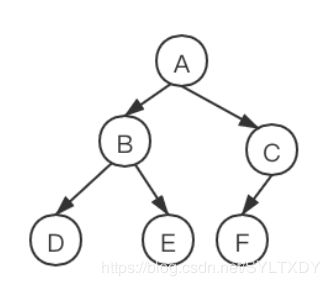
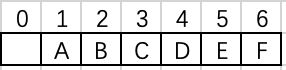
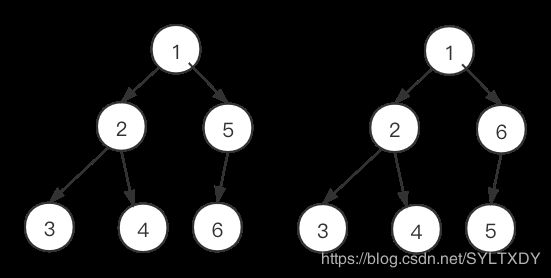
二叉堆是一棵完全二叉树,每个节点必须小于等于它的孩子节点,二叉堆可以用一个一维数组表示,如下,左儿子的位置=2*父亲位置,右儿子的位置=2*父亲位置+1
下面左图为堆,右图不为堆,因为右图的6在5上方。
堆定义:
class BinaryHeap{
private:
int size;
vector heap;
public:
BinaryHeap();
BinaryHeap(vector v);
bool empty();
int & findMin();
void insert(int x);
void deleteMin();
void up(int pos);
void down(int pos);
void decreaseKey(int p,int n);
void increaseKey(int p,int n);
void remove(int p);
void buildheap();
}; 堆操作
插入
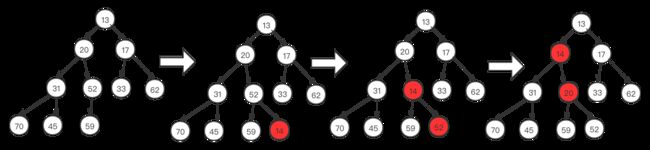
当插入一个新的元素时,将其放在堆的最后,之后和其父节点对比,如果小于父节点,和父节点对调,反复执行直到不小于父节点。这个过程叫做上滤,一个节点一直向上直到找到自己的位置。举例:如下是插入14的过程
代码:
//上滤,从hole位置开始上滤
void BinaryHeap::up(int hole){
while(heap[hole/2]>heap[hole] && hole>1){
swap(heap[hole/2],heap[hole]);
hole = hole/2;
}
}
//插入
void BinaryHeap::insert(int x){
int hole = ++size;
heap.push_back(x);
up(hole);
}删除(最小元)
将堆中最后一个元素放在根节点,并且删除最后一个元素。选择左右子树中更小的一个,并且小于根节点,和根节点替换,逐步向下,直到没有替换的。举例:
代码:
//下滤,从pos处开始下滤
void BinaryHeap::down(int pos){
while(pos*2<=size){
if(pos*2+1<=size){
if(heap[pos*2]>=heap[pos] && heap[pos*2+1]>=heap[pos])
break;
if(heap[pos*2]>=heap[pos*2+1]){
swap(heap[pos],heap[pos*2+1]);
pos = pos*2+1;
}
else{
swap(heap[pos],heap[pos*2]);
pos = pos*2;
}
}
else{
if(heap[pos*2]降低值
将位置p处的值改小,之后要上滤,例如,将下面的22减少为12,之后要进行上滤
代码:
void BinaryHeap::decreaseKey(int p, int n){
heap[p] = heap[p]-n;
up(p);
}增加值
将位置p处的值增加,之后下滤
代码:
void BinaryHeap::increaseKey(int p, int n){
heap[p] = heap[p]+n;
down(p);
}删除
删除位置p上的元素,首先用decreaseKey,将元素减小一个INF(非常大的值),之后deleteMin()
代码:
void BinaryHeap::remove(int p){
decreaseKey(p, INF);
deleteMin();
}构建堆(将一个无序的二叉树变为堆)
代码:
//堆类堆构造函数,用一个vector来构造初始堆
BinaryHeap::BinaryHeap(vectorv){
for(int i=0;i0;i--){
down(i);
}
} 标准模板库的priority_queue
优先队列的构造
//默认构造大顶堆
priority_queue heap;
//构造小顶堆
priority_queue,greater> heap;
//自定义比较
struct cmp{
bool operator()(int a,int b)
return a,cmp> heap;
//用数组初始化
int num[] ={1,5,6};
priority_queue heap(num,num+3); 成员函数
int num[] ={1,5,6};
priority_queue heap(num,num+3);
//返回队列元素个数
heap.size();
//判断队列是否为空
heap.empty();
//返回堆顶元素(队头元素)
heap.top();
//插入新元素
heap.push(4);
//插入新元素
heap.emplace(3);
//弹出堆顶元素
heap.pop();
//交换两个队列中的元素
heap.pop(heap1); 用到优先队列的例题
UVA 11997
思路:
先考虑两组数,各取其中一个,组成前k个最小的树
a = {a1, a2, a3, a4}, b = {b1, b2, b3, b4},a和b已经全部从小到大排好序
如果有3组数,第三组为:c = {c1, c2, c3, c4},假设上边前4个最小的组合构建为 ab = {a1+b1, a1+b2, a2+b1, a2+b2},那么对于ab和c两个数组做同样的操作,得出前k个最小的组合就是三组数中的最小组合。
有n组数也是同理。
以{1,5,8; 2,5,9; 6,7,10}为例。
空数组 temp,现在处理的是前两组数{1,5,8; 2,5,9}
优先队列 q = {1+2, 5+2, 8+2}, 弹出最小值放入temp,temp={3},压入1+5,
q = {1+5,5+2,8+2},弹出,temp = {3,6}, 压入1+9
q = {5+2, 8+2, 1+9}, 弹出,temp = {3, 6, 7},结束第一轮
空数组temp1,现在处理的是temp和{6,7,10}
优先队列q = {3+6,6+6,7+6}, 弹出,temp1 = {9},压入3+7
q = {3+7,6+6,7+6},弹出,temp1 = {9,10},压入3+10
q = {6+6,6+7,3+10},弹出,temp1 = {9, 10,12},结束
代码:
#include
#include
#include
#include
#include
using namespace std;
typedef struct Node{
int s;
int a;//a是第一个数的位置
int b;//b是第二个数的位置
//比如a1+b2,a就记录了1,b就记录了2
Node(int aa,int bb,int ss){
a = aa;
b = bb;
s = ss;
}
bool operator < (const Node a) const{
return s>=a.s;//小顶堆
}
}Node;
int main(){
int k;
while(cin>>k){
int number[k][k];//k组数记录在number[k][k]中
int best_k[k][k];//best_k记录每次两个数组的前k个最小组合
for(int i=0;i>number[i][j];
sort(number[i],number[i]+k);//对每组数排序
}
for(int i=0;i q;
for(int i=0;i