之前学过一些单源最短路算法,跑得非常快,但是对于SPFA这个东东,虽然它出过幺蛾子,但是在题解区发现还是很多人用,但是今天自己在做题的时候发现它还是有用,呼吁大家最好还是学学,不要有啥偏见,虽然Dijkstra确实很香。直接用例题来讲
但是本蒟蒻对于反向图的了解还并不多,如果之后学到更多的东西会继续更新
P1629 邮递员送信
我们从一个点跑出去,然后出题人 像个睿智一样 还要再跑回起点之后才能去其他地方,这么一看,这不就是Floyd的吗,但是那个时间复杂度不敢想象,直接给你T飞
换个思路,对于每一次出去,我们跑一次单源最短路其实就够了,但是对于跑回来,我们就需要跑n次最短路,非常暴力,时间复杂度也不怎么样
#include
using namespace std;
int n,m,u,v,w,tot,ans,sum[200010];
int dis[200010],vis[200010],head[200010];
priority_queue > shan;
struct node {
int to,net,val;
} e[200010];
inline void add(int u,int v,int w) {
e[++tot].val=w;
e[tot].to=v;
e[tot].net=head[u];
head[u]=tot;
}
inline void dijkstra(int s) {
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s]=0;
shan.push(make_pair(0,s));
while(!shan.empty()) {
int x=shan.top().second;
shan.pop();
if(vis[x]) continue;
vis[x]=1;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
shan.push(make_pair(-dis[v],v));
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
for(register int i=2;i<=n;i++) {
dijkstra(i);
ans+=dis[1];
}
dijkstra(1);
for(register int i=2;i<=n;i++) ans+=dis[i];
printf("%d",ans);
return 0;
}
只有40分,这个时候就可以建反向图啦
什么意思呢?我们对于跑出去的情况,一次最短路就够了,这个地方没什么好优化的,主要是从其他地方跑回来,这个时候就可以建反向图啦
以下是一个正常的有向图,我们将所有边反转一下(多开一倍空间单独存储),但这里不是建双向边,是有区别的,不然想都不用想肯定出错,这样我们就可以在多的那一倍空间中处理回来的情况,把从别的地方回来也改为过去,就只需要跑一次最短路。下面这个图的前一种情况就是处理其他点跑回来的情况,处理成第二种情况后就只需要跑一次,但是对于图中有双向边的情况,也要进行处理(和上面那句话区别一下)
#include
using namespace std;
const int MAXN=1e5+50;
struct node {
int to,net,w;
}e[2*MAXN];
int head[2*MAXN],tot;
void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].net=head[u];
head[u]=tot;
e[tot].w=w;
}
int n,m,s;
int d[2*MAXN];
bool v[2*MAXN];
priority_queue< pair > q;
void dij(int s){
memset(d,0x3f,sizeof d);
memset(v,false,sizeof v);
d[s]=0;
q.push(make_pair(0,s));
while(!q.empty()){
int x=q.top().second;
q.pop();
if(v[x]==true) continue;
v[x]=true;
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z){
d[y]=d[x]+z;
q.push(make_pair(-d[y],y));
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v+n,u+n,w); //多开一倍空间处理反向边
}
dij(1);
int ans=0;
for(register int i=2;i<=n;i++) ans+=d[i]; //过去
dij(1+n);
for(register int i=n+1;i<=2*n;i++) ans+=d[i]; //回来
cout< 又是一波三倍经验,爽啊!!!
P1342 请柬
SP50 INCARDS - Invitation Cards
对于反向图讲解目前就先到这里啦
鸽子被高温炖了之后回来更新了
P2296 寻找道路
看到题目,直接莽了一个Dijkstra最短路,然后样例直接输出2,心态爆炸。回去看题,发现有一个 路径上的所有点的出边所指向的点都直接或间接与终点连通,说明这道题我们需要加一些特殊的处理
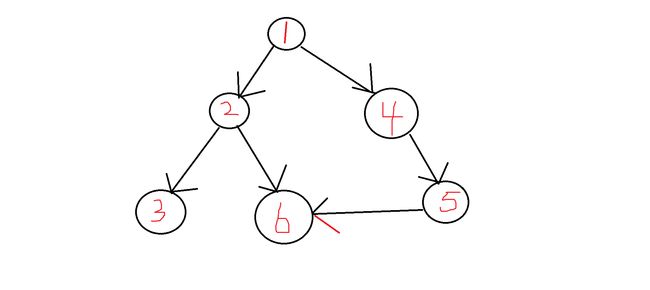
对于以上这一张图,我们直接跑最短路会是 1->2->6 答案是2,但是因为题意,我们不能走2这个点,因为2的节点3不与6连通,所以我们只能走 1->4->5->6 答案是3。那我们怎么处理这种情况呢,我们可以反向建边,然后从终点跑,能跑的地方就先用一个ok数组赋值为true
这样之后还没有结束,我们还需要进行一次check操作,如果你的儿子节点跑不到终点,那么你也跑不到,如图,3到达不了6,那么2我们也不能走,在这里我们可以再开一个数组记录,然后跑一遍最短路就可以了
#include
using namespace std;
const int MAXN=1e6+50;
int n,m;
struct node{
int net,to,w;
}e[2*MAXN];
int head[2*MAXN],tot;
void add(int u,int v,int w){
e[++tot].net=head[u];
e[tot].to=v;
e[tot].w=w;
head[u]=tot;
}
int d[2*MAXN];
bool v[2*MAXN];
bool ok[2*MAXN];
bool en[2*MAXN];
void dfs(int s){
ok[s-n]=1; //走得到,说明可以走
int i;
for(i=head[s];i;i=e[i].net)
if(!ok[e[i].to-n])dfs(e[i].to); //继续搜
}
void check(int s){
int i;
if(ok[s]==false) en[s]=false; //走不到,说明肯定是false
else
for(i=head[s];i;i=e[i].net){
if(ok[e[i].to]==false){ //如果儿子是false,父亲肯定也是false
en[s]=false;
break;
}
}
}
int s,t;
void spfa(int s){
int i,x,y,z;
queue q;
for(i=1;i<=n;i++) d[i]=20050305;
q.push(s);
d[s]=0;
v[s]=true;
while(!q.empty()){
x=q.front();
q.pop();
for(i=head[x];i;i=e[i].net){
y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z&&en[y]==true){ //这个点可以用才更新最短路
d[y]=d[x]+z;
if(v[y]==false){
v[y]=true;
q.push(y);
}
}
}
v[s]=false;
}
}
int main(){
scanf("%d%d",&n,&m);
int i;
for(i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v,1);
add(v+n,u+n,1); //开个两倍反向建边
}
scanf("%d%d",&s,&t);
dfs(t+n); //处理ok数组(不能与重点连通的点)
for(i=1;i<=n;i++) en[i]=true; //初始化
for(i=1;i<=n;i++) check(i); //再检查一次,把不能走的点标记
spfa(s); //跑最短路
if(d[t]!=20050305) cout< 回来继续更新。。。
P3916 图的遍历
非常弱智,看到题目如此的简洁,题意如此的简单,果断暴力起手(算是养成一些习惯吧,考试的时候还是暴力先拿分,正解有些时候有点浪费时间),图的遍历的话,直接dfs就好了(60分)
#include
using namespace std;
const int MAXN=1e6+50;
int head[MAXN],tot;
struct node{
int net,to;
}e[MAXN];
void add(int u,int v){
e[++tot].net=head[u];
e[tot].to=v;
head[u]=tot;
}//链式前向星建边
int n,m;
int ans;
bool v[MAXN];
void dfs(int s){
ans=max(ans,s);//找遍历到的最大值
v[s]=true;//已经走过
for(register int i=head[s];i;i=e[i].net){
if(v[e[i].to]==false){
dfs(e[i].to); //如果没有走过继续向下遍历
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
}//输入建边
for(register int i=1;i<=n;i++){
memset(v,false,sizeof v); //每一次遍历记得初始化
ans=i; //自己初始化为自己
dfs(i);//开始遍历
printf("%d ",ans);
}
return 0;
}
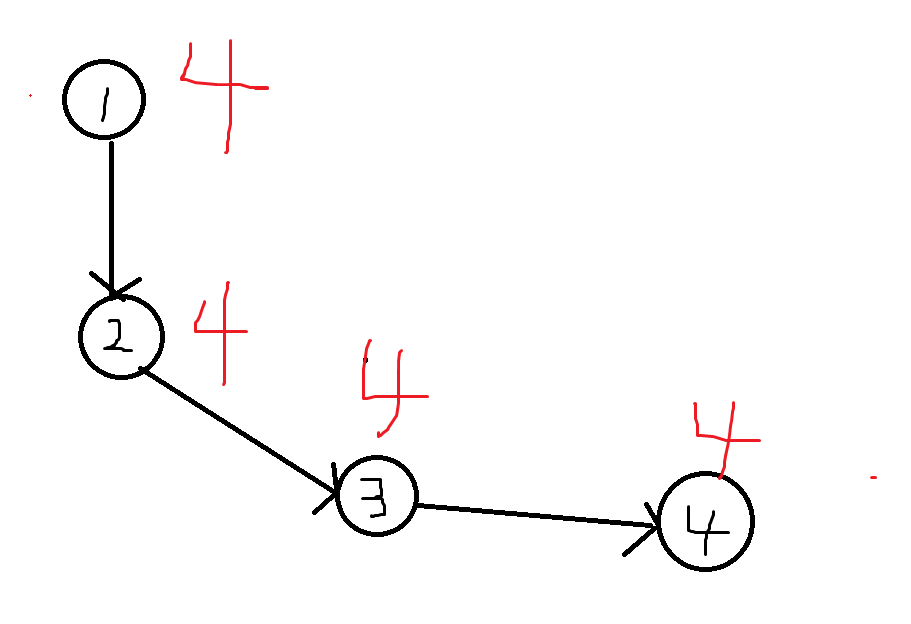
对于超时了的点,其实我们不难想出为什么超时,因为有些节点重复更新和遍历了,如图(非样例):
对于下面这一种情况,我们1,2,3的答案其实都可以由4得出,因为有传递性,所以12,3能到达的节点4都可以到达,那么我们就可以反向建边了
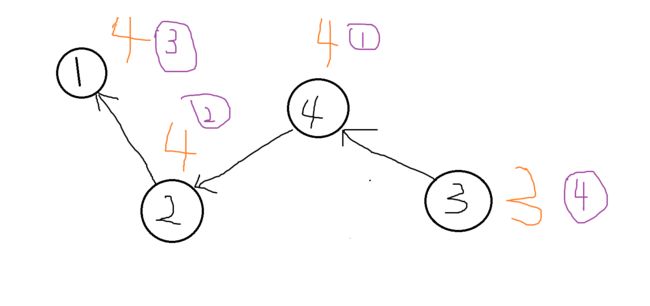
所以对于样例,我们就可以在反向建边之后,从最大点开始处理,对于已经处理了的点,就不能继续走下去(紫色的表示得出答案的顺序),因为4,2,1都先被遍历过了,说明3不能走到4,所以3的答案就是3自己
那么程序也就很好地写出来了
#include
using namespace std;
const int MAXN=1e6+50;
int head[MAXN],tot;
int n,m,dis[MAXN];
struct node{
int net,to;
}e[MAXN];
void add(int u,int v){
e[++tot].net=head[u];
e[tot].to=v;
head[u]=tot;
}//链式前向星建边
bool vis[MAXN];
inline void dfs(int k){
for(register int i=head[k];i;i=e[i].net){
if(dis[e[i].to]==0&&vis[e[i].to]==false){ //如果没有被遍历过
vis[e[i].to]=true; //标记
dis[e[i].to]=dis[k]; //赋值,因为是从最大点开始遍历,之后的答案肯定就是出发时的点
dfs(e[i].to); //向下遍历
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
add(v,u);//注意是反向建边
}
for(register int i=n;i>=1;i--) //从最大点开始遍历
if(dis[i]==0) dis[i]=i,dfs(i); //如果没有被遍历过就从这里出发开始遍历
for(register int i=1;i<=n;i++)
printf("%d ",dis[i]);
return 0;
}