4*4矩阵一般也叫齐次矩阵,主要有两个作用,描述平移变换,描述透视投影变换
4*4平移矩阵
3*3矩阵可以用来旋转,缩放坐标系,但不能移动坐标系
需要在4维空间切变实现3维平移(比较容易理解的是在3维空间实现2维平移)
而4*4平移矩阵不会影响旋转,缩放功能,所以4*4矩阵能包含旋转,缩放,平移坐标系功能
4D向量中w分量能“开关”4*4矩阵的平移部分,有些向量代表位置,应当平移,有些向量代表方向(如表面法向量),从几何意义上说,第一类数据当作点,第二类当作向量
透视投影
齐次向量:
比正常向量多了1维w,xyz除w即可转换成正常向量描述

齐次坐标(系):
上面公式左边对应图1笛卡尔坐标系,右边对应图2图3齐次坐标系 ,两者通过除w转换,描述空间坐标的两种方法,齐次坐标主要描述透视关系

4*4齐次矩阵(透视投影矩阵):
用来做透视投影转换,非线性变换最简单转换过程(向透视视图的一个面投影):
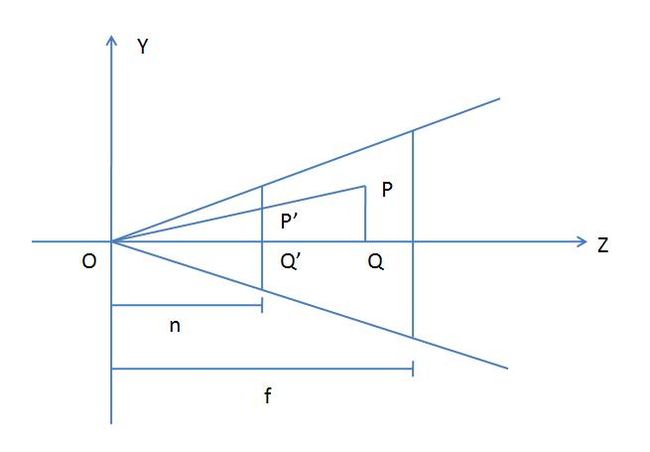
原始笛卡尔坐标P1
从笛卡尔坐标计算透视投影映射后P2
然后从这个P2找到P2的齐次坐标描述P3
然后根据原始P1的坐标和P3的齐次坐标构建一个直接从P1到P3的转换矩阵M(透视投影矩阵)
所以P1或者其他任何笛卡尔坐标系中的点D1乘以M完成了2件事,
1计算出了投影后的坐标D3,2并且这个D3坐标用齐次坐标描述
D3向笛卡尔坐标系转换只需要xyz除w
既然对于任何一点,这个矩阵都能转换成投影后的齐次坐标描述,那么相当于这个矩阵把原来的(相机)笛卡尔坐标系转换到了(透视,裁剪)齐次坐标系描述
(旋转矩阵就是这个道理,可以理解为点旋转,也可以理解为点不动坐标轴旋转后,在新的坐标系对原来点位置重新描述)
为什么要使用4*4齐次矩阵
把投影过程表示为变换,可以跟4*4矩阵进行乘法连接,表示多个变换的组合缩放矩阵只能做线性投影,而4*4齐次矩阵可以做非线性的透视投影
图形学中透视投影变换
opengl描述
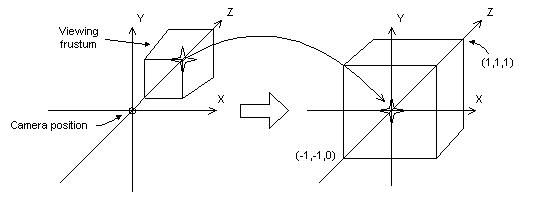
透视投影的目的就是将上面的棱台转换为一个立方体(cuboid),转换后,棱台的前剪裁平面的右上角点变为立方体的前平面的中心(下图中弧线所示)。由图可知,这个变换的过程是将棱台较小的部分放大,较大的部分缩小,以形成最终的立方体。这就是投影变换会产生近大远小的效果的原因。变换后的x坐标范围是[-1, 1],y坐标范围是[-1, 1],z坐标范围是[0, 1](OpenGL略有不同,z值范围是[-1, 1])。
具体方法 http://blog.csdn.net/onafioo/article/details/53811747