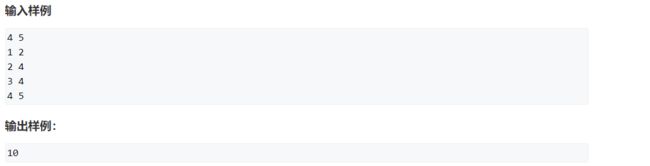
- C语言如何定义宏函数?
小九格物
c语言
在C语言中,宏函数是通过预处理器定义的,它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为,但它们不是真正的函数,因为它们在编译时不会进行类型检查,也不会分配存储空间。宏函数的定义通常使用#define指令,后面跟着宏的名称和参数列表,以及宏展开后的代码。宏函数的定义方式:1.基本宏函数:这是最简单的宏函数形式,它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
- 2021年12月19日,春蕾教育集团团建活动感受——黄晓丹
黄错错加油
感受:1.从陌生到熟悉的过程。游戏环节让我们在轻松的氛围中得到了锻炼,也增长了不少知识。2.游戏过程中,我们贡献的是个人力量,展现的是团队的力量。它磨合的往往不止是工作的熟悉,更是观念上契合度的贴近。3.这和工作是一样的道理。在各自的岗位上,每个人摆正自己的位置、各司其职充分发挥才能,并团结一致劲往一处使,才能实现最大的成功。新知:1.团队精神需要不断地创新。过去,人们把创新看作是冒风险,现在人们
- 《投行人生》读书笔记
小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅,比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力,更多的是自我意识,你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议,细节,截止日期和数据很重要截止日期,一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
- ArcGIS栅格计算器常见公式(赋值、0和空值的转换、补充栅格空值)
研学随笔
arcgis经验分享
我们在使用ArcGIS时通常经常用到栅格计算器,今天主要给大家介绍我日常中经常用到的几个公式,供大家参考学习。将特定值(-9999)赋值为0,例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值(如0)Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值,其他保留原值SetNull("raster"==
- 水平垂直居中的几种方法(总结)
LJ小番茄
CSS_玄学语言htmljavascript前端csscss3
1.使用flexbox的justify-content和align-items.parent{display:flex;justify-content:center;/*水平居中*/align-items:center;/*垂直居中*/height:100vh;/*需要指定高度*/}2.使用grid的place-items:center.parent{display:grid;place-item
- linux中sdl的使用教程,sdl使用入门
Melissa Corvinus
linux中sdl的使用教程
本文通过一个简单示例讲解SDL的基本使用流程。示例中展示一个窗口,窗口里面有个随机颜色快随机移动。当我们鼠标点击关闭按钮时间窗口关闭。基本步骤如下:1.初始化SDL并创建一个窗口。SDL_Init()初始化SDL_CreateWindow()创建窗口2.纹理渲染存储RGB和存储纹理的区别:比如一个从左到右由红色渐变到蓝色的矩形,用存储RGB的话就需要把矩形中每个点的具体颜色值存储下来;而纹理只是一
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- DIV+CSS+JavaScript技术制作网页(旅游主题网页设计与制作)云南大理
STU学生网页设计
网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业:【HTML5网页期末作业(1000套)】程序员有趣的告白方式:【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面:计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
- 2020-04-12每天三百字之连接与替代
冷眼看潮
不知道是不是好为人师,有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程,就是不断连接与替代的过程。人类发现了火并应用火以后,告别了茹毛饮血的野兽般的原始生活(火烧、烹饪替代了生食)人类用石器代替了完全手工,工具的使用使人类进步一大步。类似这样的替代还有很多,随着科技的发展,有更多的原始的事物被替代,代之以更高效、更先进的技术。在近现代,汽车替代了马车,高速公路和铁路
- 人生的每一步路都算数
sheli
如果你想打工,一直靠打工赚钱,那你就会不断的希望自己变得更专业,不断的希望能够获得更好的工作机会,升职加薪。如果你的目标志不在此,而是拥有自己的企业,那你的选择就会出现差别。在认真打工的人眼里,会“不务正业”,会总是选择不同岗位,甚至放弃高薪机会。但是这背后都是有更加长远的规划。成功富人所必需的管理技能包括:1.对现金流的管理。2.对系统的管理。3.对人员的管理。所以,在没有获得这些能力之前,只要
- 没有邀请码怎么注册买手妈妈?
氧惠评测
买手妈妈怎么注册小编为大家带来买手妈妈没有邀请码怎么注册。打开买手妈妈APP,点击“马上注册”,输入邀请信息“邀请码”点击下一步,没有邀请码是登录不上的,所以这个必须要填写,那我们没有怎么办?填写成功就可以登录下一步。这里面有手机登录和淘宝登录,手机登录以后也需要用淘宝授权的,所以基本上都是淘宝登录。购物、看电影、点外卖、用氧惠APP!更优惠!氧惠(全网优惠上氧惠)——是与以往完全不同的抖客+淘客
- 阶段总结反思
轻争
马上就要进入10月份了,今天做一下前段时间的总结和反思。前段时间,日更、英语、健身、护肤坚持的比较好。阅读、书法坚持的不好。1.中间被迫停更半个多月,其余时间一直在坚持日更挑战。偶尔也有不想写的时候,就做一下摘抄。因为阅读(输入)没跟上来,所以写作(输出)质量有待进一步加强。2.英语做到了一周至少学习5天,每次不少于30分钟,但是小班课没有跟上更新速度,下一步要争取利用零碎时间补听小班课。3.减肥
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(4)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例:文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片(Slicing)操作**基本切片语法
- 【华为OD技术面试真题 - 技术面】-测试八股文真题题库(1)
算法大师
华为od面试python算法前端
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.黑盒测试和白盒测试的区别2.假设我们公司现在开发一个类似于微信的软件1.0版本,现在要你测试这个功能:打开聊天窗口,输入文本,限制字数在200字以内。问你怎么提取测试点。功能测试性能测试安全性测试可用性测试跨平台兼容性测试网络环境测试3.接口测试的工具你了解哪些
- 高级 ECharts 技巧:自定义图表主题与样式
SnowMan1993
echarts信息可视化数据分析
ECharts是一个强大的数据可视化库,提供了多种内置主题和样式,但你也可以根据项目的设计需求,自定义图表的主题与样式。本文将介绍如何使用ECharts自定义图表主题,以提升数据可视化的吸引力和一致性。1.什么是ECharts主题?ECharts的主题是指定义图表样式的配置项,包括颜色、字体、线条样式等。通过预设主题,你可以快速更改图表的整体风格,而自定义主题则允许你在此基础上进行个性化设置。2.
- 2019-3-23晨间日记
红红火火小耳朵
今天是什么日子起床:7点40就寝:23点半天气:有太阳,不过一会儿出来一会儿进去特别清爽的凉意,还蛮舒服的心情:小激动要给女朋友过生日啦纪念日:田田女士过生日任务清单昨日完成的任务,最重要的三件事:1.英语一对一2.运动计划3.认真护肤习惯养成:调整状态周目标·完成进度英语七天打卡(5/7)轻课阅读(87/180)音标课(25/30)读书(福尔摩斯一章)学习·信息·阅读#英语课#Cookingte
- 直返APP是什么?直返APP是干嘛的
氧惠帮朋友一起省
直返是一种电商购物模式,其核心特点是用户购买商品后可以获得直接返利。具体来说,用户在直返电商平台购买商品时,不仅可以获得商品本身的优惠,还可以获得一定的现金返利或者积分奖励。返利的金额可以提现到用户的账户余额,或者用于下次购物时抵扣。氧惠APP(带货领导者)——是与以往完全不同的抖客+淘客app!2023全新模式,我的直推也会放到你下面。主打:带货高补贴,深受各位带货团队长喜爱(每天出单带货几十万
- 直返的东西正品吗?直返APP安全吗?直返是正规平台吗?
氧惠购物达人
亲们,你们是不是经常在直返APP上买东西呀?但是,你们有没有想过,里面的东西到底是不是正品呢?这个APP安全吗?它是不是一个正规的平台呀?别着急,今天我就来给大家揭秘一下!氧惠APP(带货领导者)——是与以往完全不同的抖客+淘客app!2023全新模式,我的直推也会放到你下面。主打:带货高补贴,深受各位带货团队长喜爱(每天出单带货几十万单)。注册即可享受高补贴+0撸+捡漏等带货新体验。送万元推广大
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(1)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归(LinearRegression)模型形式:关键点:逻辑回归(LogisticRegression)模型形式:关键点:参数估计与评估:3.python浅拷贝及深拷贝浅拷贝(Shal
- 读《人间鲁迅》有感
琳语读书
上周读完《闻一多传》后,我对中国近代知识分子产生了兴趣,这周继续读了《人间鲁迅》。厚厚的两本书,记录了一个人的一生,苦痛,彷徨和挣扎,虽然只读了一小部分,却也心潮澎湃。闻一多和鲁迅是完全不同的。鲁迅是沉郁的,现实的,寂寞的,抗争的。除了天生性格的不同外,环境的塑造也是非常之大。鲁迅少年经历了家庭的变故,看尽了人间冷暖,世态炎凉。这种经历促使他很早就观察思考人生,立志用文学来改变中国国民的劣根。闻一
- 渝婧感恩日记第68天
梁渝婧lydia
1.哇!我真是太幸福啦!感恩奇迹感恩训练营毕业典礼,让我能共振到同学们的喜悦和能量,感谢!感谢!感谢!2.哇!我真是太幸福啦!感恩每天早起,运动3公里!这个星期又做到连续三天,不间断!感谢亲爱的渝婧!你真的是非常的棒!加油,继续坚持!感谢!感谢!感谢!3.哇!我真是太幸福啦!感恩曾正波班主任给我们分享的艾宾浩斯的记忆曲线255学习法,让我蠢蠢欲试,感谢!感谢!感谢!4.哇!我真是太幸福啦!感恩胜利
- 南美洲的奇特艺术品【神秘档案馆·第三期】
清风小和尚
本期回答问题:1.复活节岛石像是谁建造的?2.复活节岛石像的建造方法与目的?3.纳斯卡线条的设计意义?南美洲是南亚美利加洲的简称,位于西半球的南部,东濒大西洋,西临太平洋,北滨加勒比海,南隔德雷克海峡与南极洲相望。对南美洲最简单的定位方法是:美国南面。南美洲是地球上第四大的大洲,有着种类繁多的物种和丰富的地形。在这片广袤的土地上,有两样奇特的艺术品---复活节岛摩艾石像与纳斯卡线条。摩艾石像(Mo
- 中原焦点团队网络初中级30期阴丽丽坚持分享第三百八十八次2022.10.18分享 约练次数(74) 咨询师(6) 来访者(53) 观察者(15)
阴丽丽
今天是忙碌的一天,一早起来,总想着找点把事情弄完,可总也弄不完。就这样弄着吧!孩子的事,自己的事都在那里搁置着,不想做,有点欧!今天总体还不错,只是在下午起床时走神了俩小时,也算是给自己的放松吧!今日难得1.儿子乖巧、听话,努力配合,一天下来也是忙忙碌碌,这真的很难得!2.儿子今天录的视频被班主任认可,这真的很难得3.我今天早上做核酸时,自己把教案整了一下,这真的很难得
- 简单了解 JVM
记得开心一点啊
jvm
目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称,意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统(如:JVM、VMwave、VirtualBox)。JVM和其他两个虚拟机
- 一文掌握python常用的list(列表)操作
程序员neil
pythonpython开发语言
目录一、创建列表1.直接创建列表:2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素,索引从0开始:2.还可以使用切片操作访问列表的一部分:三、修改列表元素四、添加元素1.append():在末尾添加元素2.insert():在指定位置插入元素五、删除元素1.del:删除指定位置的元素2.remove():删除指定值的第一个匹配项3.pop():
- Java企业面试题3
马龙强_
java
1.break和continue的作用(智*图)break:用于完全退出一个循环(如for,while)或一个switch语句。当在循环体内遇到break语句时,程序会立即跳出当前循环体,继续执行循环之后的代码。continue:用于跳过当前循环体中剩余的部分,并开始下一次循环。如果是在for循环中使用continue,则会直接进行条件判断以决定是否执行下一轮循环。2.if分支语句和switch分
- 《感恩日志》第八天
祖乐
1.感恩武老师给姑娘朋友的宝宝起了名字。2.感恩张淑珍老师及时发的红包让我和杜姐能按时听课学习。3.感恩今天所有的遇见
- Java面试题精选:消息队列(二)
芒果不是芒
Java面试题精选javakafka
一、Kafka的特性1.消息持久化:消息存储在磁盘,所以消息不会丢失2.高吞吐量:可以轻松实现单机百万级别的并发3.扩展性:扩展性强,还是动态扩展4.多客户端支持:支持多种语言(Java、C、C++、GO、)5.KafkaStreams(一个天生的流处理):在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制:Kafka进行生产或者消费的时候会
- 【六项精进】20180930
Kinnfoo
一、学习与实践1.付出不亚于任何人的努力2.要谦虚,不要骄傲3.要每天反省4.活着,就要感谢5.积善行,思利他6.不要有感性的烦恼二、今日分享今天是9月的最后一个工作日,每个支行都在拼命地冲刺业绩,刚好今天同桌休假了,我就替他审核客户。一个上午就进件了6个客户,审核通过5个。这5个审核通过的客户里,1个因费率没谈拢而放弃,1个因车上发现GPS而被拒单,最终确认可放款的只有3个客户。感叹支行同事的不
- 数据结构 | 栈和队列
TT-Kun
数据结构与算法数据结构栈队列C语言
文章目录栈和队列1.栈:后进先出(LIFO)的数据结构1.1概念与结构1.2栈的实现2.队列:先进先出(FIFO)的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中,栈和队列是两种基本且重要的数据结构,它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
- ASM系列五 利用TreeApi 解析生成Class
lijingyao8206
ASM字节码动态生成ClassNodeTreeAPI
前面CoreApi的介绍部分基本涵盖了ASMCore包下面的主要API及功能,其中还有一部分关于MetaData的解析和生成就不再赘述。这篇开始介绍ASM另一部分主要的Api。TreeApi。这一部分源码是关联的asm-tree-5.0.4的版本。
在介绍前,先要知道一点, Tree工程的接口基本可以完
- 链表树——复合数据结构应用实例
bardo
数据结构树型结构表结构设计链表菜单排序
我们清楚:数据库设计中,表结构设计的好坏,直接影响程序的复杂度。所以,本文就无限级分类(目录)树与链表的复合在表设计中的应用进行探讨。当然,什么是树,什么是链表,这里不作介绍。有兴趣可以去看相关的教材。
需求简介:
经常遇到这样的需求,我们希望能将保存在数据库中的树结构能够按确定的顺序读出来。比如,多级菜单、组织结构、商品分类。更具体的,我们希望某个二级菜单在这一级别中就是第一个。虽然它是最后
- 为啥要用位运算代替取模呢
chenchao051
位运算哈希汇编
在hash中查找key的时候,经常会发现用&取代%,先看两段代码吧,
JDK6中的HashMap中的indexFor方法:
/**
* Returns index for hash code h.
*/
static int indexFor(int h, int length) {
- 最近的情况
麦田的设计者
生活感悟计划软考想
今天是2015年4月27号
整理一下最近的思绪以及要完成的任务
1、最近在驾校科目二练车,每周四天,练三周。其实做什么都要用心,追求合理的途径解决。为
- PHP去掉字符串中最后一个字符的方法
IT独行者
PHP字符串
今天在PHP项目开发中遇到一个需求,去掉字符串中的最后一个字符 原字符串1,2,3,4,5,6, 去掉最后一个字符",",最终结果为1,2,3,4,5,6 代码如下:
$str = "1,2,3,4,5,6,";
$newstr = substr($str,0,strlen($str)-1);
echo $newstr;
- hadoop在linux上单机安装过程
_wy_
linuxhadoop
1、安装JDK
jdk版本最好是1.6以上,可以使用执行命令java -version查看当前JAVA版本号,如果报命令不存在或版本比较低,则需要安装一个高版本的JDK,并在/etc/profile的文件末尾,根据本机JDK实际的安装位置加上以下几行:
export JAVA_HOME=/usr/java/jdk1.7.0_25
- JAVA进阶----分布式事务的一种简单处理方法
无量
多系统交互分布式事务
每个方法都是原子操作:
提供第三方服务的系统,要同时提供执行方法和对应的回滚方法
A系统调用B,C,D系统完成分布式事务
=========执行开始========
A.aa();
try {
B.bb();
} catch(Exception e) {
A.rollbackAa();
}
try {
C.cc();
} catch(Excep
- 安墨移动广 告:移动DSP厚积薄发 引领未来广 告业发展命脉
矮蛋蛋
hadoop互联网
“谁掌握了强大的DSP技术,谁将引领未来的广 告行业发展命脉。”2014年,移动广 告行业的热点非移动DSP莫属。各个圈子都在纷纷谈论,认为移动DSP是行业突破点,一时间许多移动广 告联盟风起云涌,竞相推出专属移动DSP产品。
到底什么是移动DSP呢?
DSP(Demand-SidePlatform),就是需求方平台,为解决广 告主投放的各种需求,真正实现人群定位的精准广
- myelipse设置
alafqq
IP
在一个项目的完整的生命周期中,其维护费用,往往是其开发费用的数倍。因此项目的可维护性、可复用性是衡量一个项目好坏的关键。而注释则是可维护性中必不可少的一环。
注释模板导入步骤
安装方法:
打开eclipse/myeclipse
选择 window-->Preferences-->JAVA-->Code-->Code
- java数组
百合不是茶
java数组
java数组的 声明 创建 初始化; java支持C语言
数组中的每个数都有唯一的一个下标
一维数组的定义 声明: int[] a = new int[3];声明数组中有三个数int[3]
int[] a 中有三个数,下标从0开始,可以同过for来遍历数组中的数
- javascript读取表单数据
bijian1013
JavaScript
利用javascript读取表单数据,可以利用以下三种方法获取:
1、通过表单ID属性:var a = document.getElementByIdx_x_x("id");
2、通过表单名称属性:var b = document.getElementsByName("name");
3、直接通过表单名字获取:var c = form.content.
- 探索JUnit4扩展:使用Theory
bijian1013
javaJUnitTheory
理论机制(Theory)
一.为什么要引用理论机制(Theory)
当今软件开发中,测试驱动开发(TDD — Test-driven development)越发流行。为什么 TDD 会如此流行呢?因为它确实拥有很多优点,它允许开发人员通过简单的例子来指定和表明他们代码的行为意图。
TDD 的优点:
&nb
- [Spring Data Mongo一]Spring Mongo Template操作MongoDB
bit1129
template
什么是Spring Data Mongo
Spring Data MongoDB项目对访问MongoDB的Java客户端API进行了封装,这种封装类似于Spring封装Hibernate和JDBC而提供的HibernateTemplate和JDBCTemplate,主要能力包括
1. 封装客户端跟MongoDB的链接管理
2. 文档-对象映射,通过注解:@Document(collectio
- 【Kafka八】Zookeeper上关于Kafka的配置信息
bit1129
zookeeper
问题:
1. Kafka的哪些信息记录在Zookeeper中 2. Consumer Group消费的每个Partition的Offset信息存放在什么位置
3. Topic的每个Partition存放在哪个Broker上的信息存放在哪里
4. Producer跟Zookeeper究竟有没有关系?没有关系!!!
//consumers、config、brokers、cont
- java OOM内存异常的四种类型及异常与解决方案
ronin47
java OOM 内存异常
OOM异常的四种类型:
一: StackOverflowError :通常因为递归函数引起(死递归,递归太深)。-Xss 128k 一般够用。
二: out Of memory: PermGen Space:通常是动态类大多,比如web 服务器自动更新部署时引起。-Xmx
- java-实现链表反转-递归和非递归实现
bylijinnan
java
20120422更新:
对链表中部分节点进行反转操作,这些节点相隔k个:
0->1->2->3->4->5->6->7->8->9
k=2
8->1->6->3->4->5->2->7->0->9
注意1 3 5 7 9 位置是不变的。
解法:
将链表拆成两部分:
a.0-&
- Netty源码学习-DelimiterBasedFrameDecoder
bylijinnan
javanetty
看DelimiterBasedFrameDecoder的API,有举例:
接收到的ChannelBuffer如下:
+--------------+
| ABC\nDEF\r\n |
+--------------+
经过DelimiterBasedFrameDecoder(Delimiters.lineDelimiter())之后,得到:
+-----+----
- linux的一些命令 -查看cc攻击-网口ip统计等
hotsunshine
linux
Linux判断CC攻击命令详解
2011年12月23日 ⁄ 安全 ⁄ 暂无评论
查看所有80端口的连接数
netstat -nat|grep -i '80'|wc -l
对连接的IP按连接数量进行排序
netstat -ntu | awk '{print $5}' | cut -d: -f1 | sort | uniq -c | sort -n
查看TCP连接状态
n
- Spring获取SessionFactory
ctrain
sessionFactory
String sql = "select sysdate from dual";
WebApplicationContext wac = ContextLoader.getCurrentWebApplicationContext();
String[] names = wac.getBeanDefinitionNames();
for(int i=0; i&
- Hive几种导出数据方式
daizj
hive数据导出
Hive几种导出数据方式
1.拷贝文件
如果数据文件恰好是用户需要的格式,那么只需要拷贝文件或文件夹就可以。
hadoop fs –cp source_path target_path
2.导出到本地文件系统
--不能使用insert into local directory来导出数据,会报错
--只能使用
- 编程之美
dcj3sjt126com
编程PHP重构
我个人的 PHP 编程经验中,递归调用常常与静态变量使用。静态变量的含义可以参考 PHP 手册。希望下面的代码,会更有利于对递归以及静态变量的理解
header("Content-type: text/plain");
function static_function () {
static $i = 0;
if ($i++ < 1
- Android保存用户名和密码
dcj3sjt126com
android
转自:http://www.2cto.com/kf/201401/272336.html
我们不管在开发一个项目或者使用别人的项目,都有用户登录功能,为了让用户的体验效果更好,我们通常会做一个功能,叫做保存用户,这样做的目地就是为了让用户下一次再使用该程序不会重新输入用户名和密码,这里我使用3种方式来存储用户名和密码
1、通过普通 的txt文本存储
2、通过properties属性文件进行存
- Oracle 复习笔记之同义词
eksliang
Oracle 同义词Oracle synonym
转载请出自出处:http://eksliang.iteye.com/blog/2098861
1.什么是同义词
同义词是现有模式对象的一个别名。
概念性的东西,什么是模式呢?创建一个用户,就相应的创建了 一个模式。模式是指数据库对象,是对用户所创建的数据对象的总称。模式对象包括表、视图、索引、同义词、序列、过
- Ajax案例
gongmeitao
Ajaxjsp
数据库采用Sql Server2005
项目名称为:Ajax_Demo
1.com.demo.conn包
package com.demo.conn;
import java.sql.Connection;import java.sql.DriverManager;import java.sql.SQLException;
//获取数据库连接的类public class DBConnec
- ASP.NET中Request.RawUrl、Request.Url的区别
hvt
.netWebC#asp.nethovertree
如果访问的地址是:http://h.keleyi.com/guestbook/addmessage.aspx?key=hovertree%3C&n=myslider#zonemenu那么Request.Url.ToString() 的值是:http://h.keleyi.com/guestbook/addmessage.aspx?key=hovertree<&
- SVG 教程 (七)SVG 实例,SVG 参考手册
天梯梦
svg
SVG 实例 在线实例
下面的例子是把SVG代码直接嵌入到HTML代码中。
谷歌Chrome,火狐,Internet Explorer9,和Safari都支持。
注意:下面的例子将不会在Opera运行,即使Opera支持SVG - 它也不支持SVG在HTML代码中直接使用。 SVG 实例
SVG基本形状
一个圆
矩形
不透明矩形
一个矩形不透明2
一个带圆角矩
- 事务管理
luyulong
javaspring编程事务
事物管理
spring事物的好处
为不同的事物API提供了一致的编程模型
支持声明式事务管理
提供比大多数事务API更简单更易于使用的编程式事务管理API
整合spring的各种数据访问抽象
TransactionDefinition
定义了事务策略
int getIsolationLevel()得到当前事务的隔离级别
READ_COMMITTED
- 基础数据结构和算法十一:Red-black binary search tree
sunwinner
AlgorithmRed-black
The insertion algorithm for 2-3 trees just described is not difficult to understand; now, we will see that it is also not difficult to implement. We will consider a simple representation known
- centos同步时间
stunizhengjia
linux集群同步时间
做了集群,时间的同步就显得非常必要了。 以下是查到的如何做时间同步。 在CentOS 5不再区分客户端和服务器,只要配置了NTP,它就会提供NTP服务。 1)确认已经ntp程序包: # yum install ntp 2)配置时间源(默认就行,不需要修改) # vi /etc/ntp.conf server pool.ntp.o
- ITeye 9月技术图书有奖试读获奖名单公布
ITeye管理员
ITeye
ITeye携手博文视点举办的9月技术图书有奖试读活动已圆满结束,非常感谢广大用户对本次活动的关注与参与。 9月试读活动回顾:http://webmaster.iteye.com/blog/2118112本次技术图书试读活动的优秀奖获奖名单及相应作品如下(优秀文章有很多,但名额有限,没获奖并不代表不优秀):
《NFC:Arduino、Andro