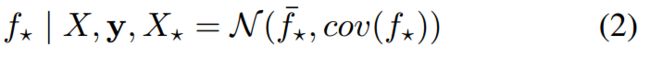【论文翻译】Laser-only road-vehicle localization with dual 2D push-broom LIDARS and 3D priors论文学习笔记

通过两个推扫式2D激光雷达和3D先验地图实现道路车辆的定位——只使用激光。

本文是2012.10年发表的EI会议（IROS）

作者：

Ian Baldwin
Department of Engineering Science
Oxford University
Oxford, UK
Email: [email protected]

Paul Newman
Department of Engineering Science
Oxford University
Oxford, UK
Email: [email protected]

 

目录

摘要

1、引言

2、相关工作

3、定位

4、位置依赖的传感器模型

5、结果

6、结论

7、未来的工作

致谢

---

摘要

本文中，展现了 仅使用2D激光雷达作为唯一传感器，借助于先验地图，在复杂、动态的真实环境中，进行准确、鲁棒、长期的道路车辆定位 的可行性。

我们使用一个双激光雷达系统——一个面向水平，以推断车辆的线性和旋转速度，一个朝向下方以捕捉周围的密集视图——这使我们可以在先验地图中同时估计速度和位置。我们展示了如何通过水平的雷达数据对充满噪声的局部速度估计进行概率建模，并对这些估计融入向下的雷达数据，以构建一个稠密的3D感知带（3D swathe），并通过统计学匹配该感知带到地图中，从而实现稳健的、长期的位置估计。

我们通过学习位置相关的传感器模型（即空间变化的传感器模型）来适应路过的车辆、行人、地面撞击（ground-strike）等引起的估计误差，并表明学习这种激光雷达数据模型可以使我们优雅地处理真实数据。我们在牛津郡伍德斯托克镇及其周围超过9公里的行驶距离验证了这一概念。

1、引言

在本文中，我们考虑使用固定的二维激光雷达进行长期导航，作为[1]中工作的扩展（[1]Road vehicle localization with 2D push-broom LIDAR and 3D priors ）。我们考虑了基于扫描匹配的定位算法（通常在室内环境中使用）在暴露于具有挑战性的真实室外环境时，容易在哪些方面导致失败。这项工作背后的动机（motivation）是生成一个简单、健壮的系统，该系统可以长期地重复使用，而不是被迫重复地为工作环境建图。

与3D传感器（例如Velodyne）相比，固定式2D激光雷达有几个固有的优势，特别是具有较低的机械复杂性和较小的物理封装。至关重要的是，在我们的方法中，其中一个激光器是朝下的，有意对路面和周围进行取样。该丰富的三维模型是由车辆在环境中运动而建立的，并在先前的地图中进行基于统计学的匹配，以生成特殊的欧几里德（SE2）姿势（位置和方向）。

考虑到真实世界的流动性和复杂性，我们认为二维平面地图缺乏准确、长期定位所需的描述信息。在这项工作中，我们利用扫描匹配的“精确相对短期一致性”来提供局部速度估计，然后将其与朝向下方的激光雷达的数据集成，构建一个丰富的地图感知带，然后将其用于基于信息的地图匹配算法中，该算法具备可重复性，可实现先验地图中的全局定位（请注意，我们不考虑SLAM问题）。图1显示了一个示例目标环境：

图1：牛津郡伍德斯托克市行驶路线概况。该路线经过许多非常不同的环境——郊区住宅（以红色突出显示，东段）、树叶茂密、坡度陡峭的地区（绿色、北部）和拥有大量行人和车辆的城镇中心（蓝色、西段和南段）。在这些非常不同的环境中精确导航是一项艰巨的任务。（本图必须以彩色查看。）

我们提出了一个构架，将利用扫描匹配的相对一致性，结合地图匹配算法中的密集的三维感知带更新，将对长期场景变化具有鲁棒性。同时，我们学习了一个基于位置的传感器模型——也就是说，一个具有空间变化固有特性的传感器模型——并表明，这样做对于短期场景变化的鲁棒性是有必要的。为了验证这一概念，我们表明，仅此激光雷达系统可以提供超过9.5公里的真实世界的数据的精确姿态估计。

2、相关工作

基于激光的道路车辆室外定位通常通过使用Velodyne 3D激光雷达部件来解决[2][3]。[4]和[5]中的作者除了利用GPS和里程计数据外，还利用了一个Velodyne来生成一个精确的路线图，然后在运行时用一个粒子滤波器进行匹配。在[6]中，作者开发了一个生成多层次表面地图的系统，用2.5d的结构来表示环境——同样用一个Velodyne来表示。在这项工作中，我们放宽了对昂贵的、复杂的传感器的需求，如Velodyne。

[7]中的作者利用固定在直升机平台上的二维激光雷达，并利用扫描匹配算法生成高质量的三维地图。虽然这项工作在思路上和我们是相似的，但作者利用了GPS和罗盘数据，这和我们的构架不同。

[8]等人利用一个稳健的ICP[9]算法，生成一个稳健的直方图特征表示，进行局部子地图匹配。虽然在这项工作中，我们使用了一个ICP导数，但它只是在开环容量中以推断相对的车辆运动。考虑到激光雷达扇面因地面撞击、来往车辆等因素产生的噪声，我们不打算直接使用ICP进行定位估算。还有许多其他的关于二维激光雷达扫描匹配实现的文献，从基于特征的方法[10]，通过极性表示的关联[11]和其他一些方法[12][13][14][15]。在本文这项工作中，我们重点学习任意扫描匹配方法的传感器过滤器，而不是开发新的扫描匹配衍生方法。

来自视觉领域的一个类似的基于视觉的系统是视觉教学和重复（Visual Teach and Repeat）[16]。在这项工作中，立体摄像机被用来建立一个多方面的世界代表，包括以前访问过的子地图（教学），然后在随后的回访中用于定位（重复）。由于摄像机的视野有限，这种方法可能会遇到相对较小的收敛盆地（convergence basin），但在这种方法（应该指的是本文的方法）中并非如此。

3、定位

我们假设事先用一辆测量车通过了工作区域——一辆装备着3D建图功能和精确位姿感知功能的车辆——因而可以生成一个3D点云，我们称之为P。我们试图根据轨迹和点云定位我们自己，点云一个源自先验的测量（点云P），一是在运行时所产生（点云Q），点云Q是通过在n秒的回顾性窗口[tk，tk-n]上构建车辆运动产生。在运行时，我们只能从水平和垂直安装的激光雷达得到数据信息。图2显示了测试车辆上传感器套件的布局，图3显示了此传感器布局下的采样扫描，以及运行时的点云：

图2：车载传感器的参考框，X、Y、Z分别为红色、绿色和蓝色。Fh对应于水平激光雷达，Fv对应于向下的激光雷达。这些激光雷达的扫描示例如图3所示。

图3：典型的运行时产生的点云（Q）的透视图，垂直和水平激光分别以蓝色和绿色突出显示。箭头指示车辆的运动——在环境中移动时生成感知带数据。在感知带中清晰可见的是窗框和建筑边缘。右上角的插图显示了车辆前保险杠视角的场景视图。运行时点云将在先验的地图P中进行匹配，以提供SE2姿态估计。

跟踪问题是——考虑到点云P和运行时得到的感知带Q，建立一个转换T，来实现点云的最优对齐。此过程分为两个部分——根据观测数据构建运行时点云Q（第III-A节），并将此点云和先前的经验点云（先验点云）P结合以生成SE2姿势（第III-B节）。

A.产生感知带Q

为了在运行时生成感知带Q（如图3中所示的），我们需要在“窗口”阶段重建车辆的相对运动。系统状态方程为：

其中v(t)是车辆框架的速度，ω(t)是车辆的转动速度。通过集成（/积分）窗口期的状态方程，我们能够生成车辆的相对运动——然而我们无从直接获得车辆的旋转速度值和直线速度值。

为了估计这些速度，我们使用迭代最近表面（ICS）算法[17]——标准迭代最近点[9]算法的一个变种——在水平激光的连续激光扫描之间执行扫描匹配。本文的重点不在于提高ICS的性能，因为我们只是在开环容量(capacity)中使用它来估计点到点的速度。

图4a所示为车辆的线速度，单位为米/秒，由ICS（蓝色）估算，由车载INS 【注释1】（红色虚线）测量，持续行驶2分钟。同样，图4b显示了估计（绿色）和实际（红色）偏航速度：

【注释1】：所用的INS系统是一个牛津技术公司的双天线3042单元，具有Omnistar HP校正功能，精度为亚分米。但是，如[1]所示，这一界限经常被越过。

图4：车辆行驶两分钟后的线性（m/s）和旋转（rad/s）速度估计值，其中ICS估计值（分别为蓝色和绿色）和地面真值（Ground Truth）（从车载INS惯性导航系统获得）为红色。

从这张图可以看出，线性和旋转速度都得到了很好的估计，但有噪声。我们试图在概率回归框架中建立底层速度模型，这是高斯过程（Gaussian Process (GP)）的自然选择[18]。如果我们将输入数据X视为时间，将输出y视为速度（线性或旋转），那么测试输入X☆的GP定义为：

其中，f☆-和cov(f☆)是平均和协方差方程：

其中，σ是给定的核函数的超参数。图5显示了一个GP训练，通过最大化图4中部分转动速度数据的边缘对数似然。

图5：图4所示的一段旋转速度数据上GP的平均函数（通过最大化边缘对数似然进行训练）。所示为1σ界限和平均函数（纯蓝色）。对比地面实况数据（红色虚线），我们发现GP平均函数捕捉了旋转速度的走势。

虽然保持线性和旋转速度的独立线程（separate processes）的计算代价很高，但是窗口特性使整个算法的复杂性保持不变（O（1））。现在我们可以估计车辆的速度了，我们把注意力转向生成点云Q。我们确定时间t的激光扫描为：

其中，rn是扫描光束n的激光距离读数（单位：米），in是强度，S = {s(1), . . . , s(n)}是一组扫描。考虑到GP平均值对速度的估计，我们现在可以整合状态方程（方程式1），为每次扫描生成SE2位姿-Xs（t）。然后我们可以从Xs（t）生成激光数据点S（t），从而生成感知带Q。将Q与P最佳对齐（/匹配）的转换将是当前的姿势X（t）。现在我们来讨论定位过程本身。

B.在先验地图中的定位

我们在此提供了定位程序的概述，这在[1]中进行了全面的描述。一旦我们在窗口期间构建了感知带，我们需要确定它与测量点云P的对齐方式。我们通过最小化目标函数f，来寻求将点云P和Q最佳对齐的转换T^：

测量（survey）中引用的感知带，是角速度和线速度剖面、激光雷达数据以及我们正在估计的转换的函数。它被分解为：

式(7)生成感知带Q，并使用转换T将其投影到全局框架中。由于P和Q是空间中点的分布，所以Kullback-Leibler散度（Kullback-Leibler divergence）是比较这些分布的相似性的自然概率方法。我们构建了以下代价函数：

其中H（.）表示柱状图操作，N是分布的基数。请注意，如果我们只需要平移和旋转，那么我们可以简单地将点向下投影到全局xy平面中，以生成柱状图。算法1概述了整个定位过程。

该算法在系统初始化时以初始位姿猜测T作为起始。然后连续运行，接收新的水平和垂直扫描数据（Sh、Sv）。水平扫描数据通过运行基于ICS的扫描-匹配器被用于估计线性和旋转速度v和Ω。一旦我们对速度进行了估计，就可以建立局部子地图Q，然后将其用于姿态估计步骤，以求解当前的最佳姿态估计T。

通过考虑感知带（swathe）的三维点与先验点云之间XY投影概率分布的KL -散度，以使目标函数最小化。这种信息理论方法使得在面对剧烈的长期场景变化时，能产生更为稳健的估计值——该方法在[1]中有详细说明。

不幸的是，上述框架对于高度动态的环境来说并不健壮。图6显示了整个Woodstock（镇名，测试地点）运行期间的速度误差图，该图是通过将INS系统的速度与扫描匹配算法获得的速度进行比较获得的。

图6：Woodstock（镇名，测试地点）运行过程中扫描-匹配算法的线速度误差图——与车辆上的商用级INS系统相比。在某些位置，误差超过6米/秒。这些误差的典型原因（如图7a至7c所示）是由纵摇和横摇（pitch and roll）引起的地面撞击（点虚线、右上角、中上角）、迎面而来的车辆（虚线、左上角）和前方道路上的车辆（点线、左下角）。我们试图开发一个位置上的扫描-匹配过滤器，可以处理这些错误的速度。

图7：（a）穿过凸起的人行横道后地面撞击（ground-strike）产生的速度误差；（b）迎面车辆的相对速度产生的速度误差；（c）前面的车辆的相对速度产生的速度误差。

从图中可看到导致扫描匹配算法性能不佳的许多区域。误差的典型原因是车辆倾斜/侧倾（pitch/roll）（图7a）、迎面而来的车辆（图7b）和自身车辆前面的车辆（图7c）。在所有这些配置中，所估计的速度为（实线）蓝色，地面真实速度为（虚线）红色。

这顺理成章地让我们相信，我们需要一个传感器模型，能够过滤出相对于车辆处于运动状态的环境区域（如激光雷达测距数据中显示出来的交通车辆、人员和地面撞击（ground-strike））。作为一个例子，图8显示了使用INS数据从水平LIDAR覆盖到公共帧的两次扫描（相隔一秒）。

图8：图7c中描述的场景的激光雷达视图。这里，移动物体之间的相对运动-警用货车（police van）、车辆和场景背景导致连续扫描中的点发生实质性移动，引起匹配的差异。一秒钟分离扫描的点（分别为红色和蓝色）被覆盖到一个全局帧中，而货车（van）的联系（correspondences）以绿色突出显示。由于货车（van）和车辆（指的是本车辆）之间的相对速度小于真实速度，因此速度估计值会相应地被抑制，正如图7c所示。

从图中可以看出，在两次激光雷达扫描之间的时间段内，大部分场景是静态的，从点重叠处可以明显看出这一点。然而，前面（警用）货车的相对速度导致了匹配的困难——这体现在对图7c相邻图中真实速度的低估。为了防止这种精度退化行为，我们寻求学习一个位置依赖的传感器模型——也就是说，一个模型这将使我们能够过滤算法所接收到的的扫描点，鉴于（/考虑到）我们知道我们在世界环境中的位置。

4、位置依赖的传感器模型

为了纠正图7a、7b和7c中的异常现象，我们需要学习一个概率过滤器，它可以让我们从所有扫描数据中删除会降低扫描-匹配算法性能的点。我们寻求一种在扫描中概率过滤点的方法，考虑到我们在世界上的位置，这将是很好的匹配候选。我们不需要为我们遇到的每一个短暂的障碍建立一个模型——只需要一种方法来判断扫描数据（scan）对应好的区域还是坏的区域。

因此，我们引入位置依赖的传感器模型的概念。考虑将输入值λ映射到某个输出空间的函数f：

假设我们正在穿越一个路网，这个映射的自然表示是一个三次样条曲线，它将一个浮点型数值映射到一个全局UTM（x，y）位置（R→R2）。

如果我们把来自激光雷达的数据看作极坐标表示的点（θ，r），则我们试图了解掩蔽概率分布p(X | Θ, r, λ)，其中Xi是表示在扫描平面中离散{θ，r}单元中观察到的激光数据的瞬态的二元变量。为了使问题易于处理，我们将学习一个模型用于沿着样条参数化的离散位置，因此需要一种学习每个离散化的联合分布p(X | Θ, r, λ)的方法。此测量捕获了来自某个单元的传感器数据的可靠性。图9描述了该模型：

图9：用于估计激光雷达扫描平面区域瞬变的模型的图形表示，给定世界环境上的某个位置——λ。未观察到的潜在状态X构成了激光雷达光束平面上某个位置的潜在瞬变。观察值y是来自训练数据的噪声估计值，通过观察连续的激光扫描中的点偏差进行估计。

这种短暂性的测量使我们能够客观地（/通过概率/概率性地）确定，我们对来自世界某个特定点的激光雷达数据能信任多少。我们注意到，在训练过程中，我们使用DGPS校正的INS数据，通过叠加连续扫描的点，观察到对扫描细胞(scan cells)瞬态性的噪声估计。然后，我们使用最近邻搜索和剔除比某个阈值更接近的点，在扫描之间生成点的对应关系。因此，其余的点肯定会在连续扫描之间大幅地移动。这个过程的结果可以在图10中看到。

然后，我们对这些观测绘制柱状图，以产生每个细胞（cell）瞬变的计数——z，然后通过以下过程将其映射到细胞（cell）瞬变的（噪声）观测中：

其中式10为广义的逻辑函数。zi构成对细胞（cell）i的观察，其中连续激光扫描的点有一定的公差，γ和δ是比例因子。这个映射函数产生一个在{+1、−1}范围内的值，并使得我们相信，即我们在一个单元中观察到的运动越多，该单元就越不可能成为一个良好的静态扫描-匹配候选源。通过将潜在瞬变和观测到的瞬变的联合分布建模为马尔可夫随机场（Markov Random-Field
，MRF），我们试图了解给定参数p(X, y | θ)的联合分布：

其中X是一组二进制标签（瞬态/非瞬态），y是噪声观测值，方程式11和12是能量和联合概率项，如[19]所示。Z是分配函数(partition function)，确保方程式12是有效的概率分布。

给定模型的一组参数，然后我们可以应用迭代条件模式（Iterated Conditional Modes (ICM)）[19]——一个贪婪的优化过程——以此来推断最可能的标签集。假设我们可以将联合分布因素考虑为：

在马尔可夫假设下，我们可以写出潜在变量Xi的分布：

式中，符号X\{i}表示除i外X的所有值。ICM，从给定的初始标记开始，贪婪地改变单个潜在变量状态，直到式14最大化。这里我们不关注参数估计问题——这表明即使有一组次优的（sub-optimal）参数集，我们也可以执行鲁棒、稳健的定位——因为这不是一个限制因素。对于图10中所示的位置上收集来的数据，X的最可能标记如图11所示。

图10：图8所示区域的瞬变观测。通过在初始运行期间融合INS和LiDAR数据，我们可以隔离环境中表现出的高度瞬变的区域。除了车辆外，还检测到地面撞击（左侧）-这是正常的，因为地面撞击可以被描述为快速移动的障碍物。有些静态结构被错误地观测为瞬变-然而，这些观测的数量很小。图（b）显示了一段近似样条曲线（灰色）和特定λ值的模型域。（本图必须以彩色查看。）

图11：通过将ICM应用于图10中所示的位置的观察数据，而在图9中描绘的模型上给出所得到的局部最大X。（The resulting locally maximal X given by applying ICM to the observed data for the location shown in Figure 10 over the model depicted in Figure 9.）。请注意，考虑到车辆的存在，道路已成为扫描-匹配（scan-matching）不可靠的地方。此外，两栋建筑之间的入口通道也被归类为瞬态-这是由于车辆在该特定点处反复发生诱导侧翻（repeated induced）。

注意，至关重要的是，我们没有明确地对车辆模型进行编码，但我们已经了解到，道路是不适用扫描匹配点的地方。我们还了解到，地面撞击也是不受欢迎的——图11将两个建筑物之间的区域划分为瞬时激光雷达数据源。这是由于在该特定区域车辆侧翻（vehicle roll）引起的反复观察到的地面打击。

我们现在在运行时使用这个分布来过滤激光雷达点，这些点有很高的概率来自一个瞬态物体，无论是车辆，还是由车辆的滚动/俯仰运动所导致的地面撞击。我们展示了这如何使我们能够在测试真实路线的先验地图中定位车辆。

5、结果

这些结果是在Woodstock镇周围9.5公里的回路轨道上（如图1所示）运行算法后获得的。图12显示了路线长度2.7公里（多次来回行驶以获得9.5公里的运行）的跟踪结果，从图中可以看出，尽管环境中有大量的瞬变，且路线中某些地方的多样性地面（copious ground）会产生有害的影响，系统还是做到了在路线长度上保持定位。

图13对比了原始的基于ICS的速度（如图7c所示）和相应的使用图11中模型的滤波后的输出。

图12：伍德斯托克（Woodstock）附近的跟踪结果。估计的轨迹以红色显示，随着时间的推移，来自地面真值的样本以蓝色显示（更密集的区域对应较慢的速度-在图像左侧可见）。系统在全程路线长度上保持完全定位（fully localized）。（本图必须以彩色查看）

图13：使用所述程序，对图7c所示情景的原始（蓝色）和过滤（绿色）速度估计进行比较。学习一个空间变化的过滤器（spatially-varying filter），它可以隔离环境中通常产生较差扫描-匹配候选的区域，从而获得更好的速度估计。

本图清楚地表明，过滤掉瞬态激光雷达数据可以得到更好的速度估计，从而实现定位。经过过滤的信号的噪声比原始信号的噪声要高一些——然而，这是硬屏蔽过程的假象，使用比例加权法很容易适应。这个问题并不重要，因为GP回归可以轻松处理稍高的噪声比。

为了进一步说明该系统的优点，我们使用与[1]中相同的度量标准。我们将轨迹中姿势x（t）的位移函数定义为：

其中，xs被定义为初始测量轨迹(the trajectory that defined the initial survey)中最接近的点。该度量(metric)将捕获初始轨迹的真实偏差，以及INS和（本文）所描述系统的定位误差。这里的关键观点是，虽然我们不会两次完全穿过同一条路线，但轨迹足够接近，方程式15将允许我们定量比较系统与高性能INS系统的性能。图14显示了在伍德斯托克（Woodstock）周围一个环路（2.7km）上，INS和（本文）所述系统的轨迹估计（相对于测量轨迹survey trajectory）的比较。

图14:INS系统（蓝色，固体）和所述系统（红色，虚线）在超过2.7km上的相对偏差（relative displacements）——和参考轨迹（reference trajectory）相比。从图中可以看出，我们的系统相对于参考轨迹（reference trajectory）的偏差（displacement）较低（除了图中所示的初始化阶段）。

如图14所示，在整个路径过程中，使用我们系统的相对偏差（relative displacements）始终低于INS（除了初始化误差）。这证实了我们的直觉，即我们不会忍受与INS相同的长期漂移（详见[1]）。图15显示了INS和双激光雷达系统（Dual-LIDAR system）在整个9.5km路线上的平均相对偏移：

图15:INS和双激光雷达系统在同一9.5公里路线上相对于参考轨迹（reference trajectory）的平均偏差（displacement）。该方框图显示，平均而言，双激光雷达系统的偏差（displacement）较小。

这一统计数据表明，平均而言，双激光雷达系统在多个回路上（on multiple loops）对参考轨迹的偏移比惯性导航系统小。

6、结论

我们提出了一个仅基于二维激光雷达数据的系统，该系统能够在一个扩展的室外路线的先验地图中进行精确定位。我们已经演示了如何使用扫描-匹配算法（scan-matching algorithm）中的局部速度估计值，并将其与车辆运动所生成的三维点数据融合，我们能够在具有挑战性的环境中为9.5公里的行驶生成良好的定位估计值。我们已经证明，学习一个空间变化的传感器模型是一个先决条件，使我们能够以一种更强大的方式估计速度，从而相应地得到更好的位置估计（positional estimates）。我们使用偏移度量（displacement metric）对商业级惯导系统和我们的系统的性能进行了定量对比，并表明从我们的系统得出的姿态估计结果，在被测试的线路上，相对于参考轨迹的偏差（displacement）较低。

 

7、未来的工作

在这项工作中，我们专注于学习位置传感器模型——然而，我们可以自由地折叠其他外部线索，这些线索告诉算法关于上下文的信息。例如，我们可以利用许多基于视觉的汽车检测框架中的一个作为概率过滤器的额外输入（以增加额外传感器为代价）。

为了开发一个独立的系统，我们专门研究了激光雷达的速度和位置估计。然而，我们可以利用车辆里程表（如果有的话）来重新确定退化区域的速度估计。

此外，我们试图了解概率滤波器（probabilistic filter）如何随时间变化-例如，季节变化对激光雷达数据的影响和交通流量的随时间的变化-这构成了未来工作的基础。

致谢

这项工作由海军再搜索局（ONR）拨款N00140810337和EPSRC拨款EP/I005021资助。