支持向量机SVM的原理和常用名称解释,以及利用sklearn-SVC实现简单的支持向量机
支持向量机(SVM)
1. 简介
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行二元分类(binary classification)的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane)。
SVM使用铰链损失函数(hinge loss)计算经验风险(empirical risk)并在求解系统中加入了正则化项以优化结构风险(structural risk),是一个具有稀疏性和稳健性的分类器。SVM可以通过核函数(kernel function)进行非线性分类,常见的核函数是径向基函数(radial bias function)。
2. 用途
支持向量机(Support Vector Machine)用于解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中。当样本数据线性可分时,解决两个变量的分类问题可以用一条直线把点给分开,完成分类。当样本数据线性不可分时,主要通过松弛变量和核函数技术来实现,这一部分是SVM的精髓。
3. 名称解释
- 线性可分:能画出一条直线将两组数据点分开。
- 分隔超平面:将数据集分隔开来的超平面。在二维中分隔超平面为直线,在三维中分隔超平面为平面,以此类推。
- 间隔:点到分隔超平面的距离。
- 支持向量:离分隔超平面最近的那些点。
- 最大数据集间隔:找到离分隔超平面最近的点,确保离分隔超平面距离尽可能远。
- 核函数:将数据从一个低维空间映射到一个高维空间,可以将一个在低维空间中的非线性问题转换成高维空间下的线性问题来求解。常用的核函数为径向基函数。
- 松弛变量:使用核函数向高维空间映射后,问题仍然是线性不可分的,则加入松弛变量。当找了两条直线,最大化它们的距离,但有时我们找的直线,它们中间有一些散落的点,这些点不满足那个限制条件。通过松弛变量使得允许一定的误分类的情况。
- 数据集偏斜:指的是参与分类的两个类别(也可以多个类别)样本数量差异很大。
- 惩罚因子C:为了解决数据集偏斜,加入惩罚因子C,C越大表示越重视离群点,越不想丢掉它。
- 序列最小优化算法(SMO):将大优化问题分解为多个小优化问题来求解。其工作原理:每次循环中选择两个alpha进行优化处理,一旦找到一对合适的alpha,则增大其中一个同时减少另一个。
4. 原理
【两类分类器——样本数据线性可分】
SVM是用来解决分类问题的,如果解决两个变量的分类问题,可以用一条直线把点给分开,完成分类。如下:
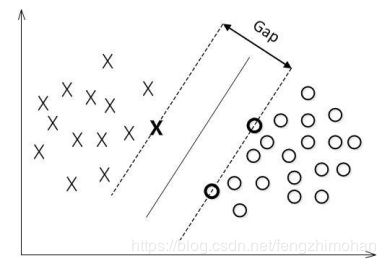
上面这些点很明显不一样,我们从中间画一条直线就可以用来分割这些点,但是什么样的直线才是最好的呢?通俗的说,就是一条直线“最能”分割这些点,也就是上图中的直线。他是最好的一条直线,使所有的点都“尽量”远离中间那条直线。总得的来说,SVM就是为了找出一条分割的效果最好的直线。怎么样找出这条直线,就变成了一个数学问题,通过数学一步一步的推导,最后转化成程序。这里举例是二个特征的分类问题,如果有三个特征,分类线就变成了分类平面,多个特征的话就变成了超平面。从这个角度出发去看待SVM,会比较轻松。
数学解决方法大致如下:
目的是求最大分隔平面,也就是选取靠近平面最近的点,使这些点到分隔平面的距离W最大,是一个典型的凸二次规划问题。

但是上面需要求解两个参数w和b;于是为求解这个问题,把二次规划问题转换为对偶问题。

这样就只需求一个参数a了,通过序列最小优化算法(Sequential Minimal Optimization SMO)求出a后,再计算出b 。
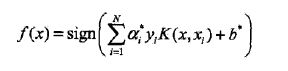
最后通过f(x)用做预测。
【两类分类器——样本数据线性不可分】
当提供的样本线性不可分,结果很简单,线性分类器的求解程序会无限循环,永远也解不出来。这必然使得它的适用范围大大缩小,而它的很多优点我们实在不原意放弃,怎么办呢?是否有某种方法,让线性不可分的数据变得线性可分呢?
通过引入核函数实现。
具体阅读:
http://www.blogjava.net/zhenandaci/archive/2009/03/06/258288.html
当将线性不可分转为线性可分后,依然存在少数点线性不可分,这种情况称为:近似线性可分。为了解决这个问题,需要引入松弛变量。
具体阅读:
http://www.blogjava.net/zhenandaci/archive/2009/03/15/259786.html
http://www.blogjava.net/zhenandaci/archive/2009/03/17/260315.html
现实中要解决的问题,往往是多类的问题,比如文本分类,比如数字识别。如何由两类分类器得到多类分类器,就是一个值得研究的问题。SVM也能用于多类分类。
具体阅读:
http://www.blogjava.net/zhenandaci/archive/2009/03/26/262113.html
5. sklearn实现
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
X = np.array([[1,1],[1,2],[1,3],[1,4],[2,1],[2,2],[3,1],[4,1],[5,1],[5,2],[6,1]
,[6,2],[6,3],[6,4],[3,3],[3,4],[3,5],[4,3],[4,4],[4,5]])
Y = np.array([1]*14+[-1]*6)
T = np.array([[0.5,0.5],[1.5,1.5],[3.5,3.5],[4,4.5]])
svc = SVC(kernel='poly',degree=2,gamma=1,coef0=0)
svc.fit(X,Y)
pre = svc.predict(T)
结果输出:
print(pre)
print(svc.n_support_)
print(svc.support_)
print(svc.support_vectors_)
[ 1 1 -1 -1]
[2 3]
[14 17 3 5 13]
[[3. 3.]
[4. 3.]
[1. 4.]
[2. 2.]
[6. 4.]]
参考文章:
1.http://www.blogjava.net/zhenandaci/category/31868.html(写的特别好,通俗易懂,思路清晰,力推!)
2.https://blog.csdn.net/csqazwsxedc/article/details/71513197
3.https://www.cnblogs.com/xiaotan-code/p/6695049.html