【CQOI 2014】危桥

【题目】

传送门

题目描述：

Alice 和 Bob 居住在一个由 $n$ 座岛屿组成的国家，岛屿被编号为 $0$ 到 $n-1$。某些岛屿之间有桥相连，桥上的道路是双向的，但一次只能供一人通行。其中一些桥由于年久失修成为危桥，最多只能通行两次。

Alice 希望在岛屿 $a_1$ 和 $a_2$ 之间往返 $a_n$ 次（从 $a_1$ 到 $a_2$ 再从 $a_2$ 到 $a_1$ 算一次往返）。同时，Bob 希望在岛屿 $b_1$ 和 $b_2$ 之间往返 $b_n$ 次。这个过程中，所有危桥最多通行两次，其余的桥可以无限次通行。请问 Alice 和 Bob 能完成他们的愿望吗？

输入格式：

本题有多组测试数据。

每组数据第一行包含 $7$ 个空格隔开的整数，分别为 $n$、$a_1$、$a_2$、$a_n$、$b_1$、$b_2$、$b_n$。

接下来是一个 $n$ 行 $n$ 列的对称矩阵，由大写字母组成。矩阵的 $i$ 行 $j$ 列描述编号 $i-1$ 和 $j-1$ 的岛屿间连接情况，若为 “O” 则表示有危桥相连；为 “N” 表示有普通桥相连；为 “X” 表示没有桥相连。

输出格式：

对于每组测试数据输出一行，如果他们都能完成愿望输出 “Yes”，否则输出 “No”。

样例数据：

输入
4 0 1 1 2 3 1
XOXX
OXOX
XOXO
XXOX
4 0 2 1 1 3 2
XNXO
NXOX
XOXO
OXOX

输出
Yes
No

备注：

【数据范围】

$4\le n\le 50$
$0\le a_1,a_2,b_1,b_2\le n-1$
$1\le a_n,b_n\le 50$

【分析】

不错的网络流的题。

很容易想到的是，从源点向 $a_1,b_1$ 连容量为 $a_n,b_n$ 的边，从 $a_2,b_2$ 向汇点连容量为 $a_n,b_n$ 的边，普通桥就连 $inf$ 的边，危桥连 $1$ 的边（因为是来回），然后跑最大流判断是否满流就行了。

但是这样是错的，反例如下：

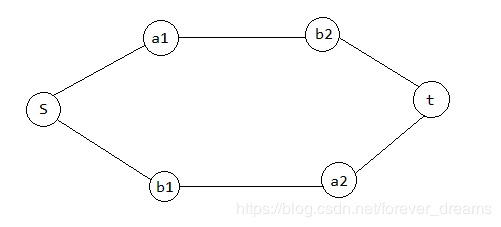
这张图的意思是，$b_2\to t$ 的部分流量可能是来自 $a_1$ 的，同理 $a_2\to t$ 的部分流量可能来自 $b_1$，这样肯定不合题意。

解决方案是，交换 $b_1,b_2$，重新建图，再跑最大流。只有两次均满流才存在可行方案。

以下内容摘抄自 SovietPower

• 假设第二次满流仍然存在这种问题。
• 假设第一次跑最大流，$a_1\to b_2$ 的流量为 $x$，那么 $b_1\to b_2$ 的流量为 $b_n-x$，$b_1\to a_2$ 的流量也是 $x$，$a_1\to a_2$ 的流量是 $a_n-x$ 。
• 而第二次跑最大流，因为是无向图，$a_1\to a_2$ 和 $b_2\to b_1$ 的流量可以不变，还是 $a_n-x,b_n-x$ 。那么 $a_1\to b_2$ 和 $b_2\to a_1$ 的流量也都还是 $x$ 。
• 而这两次说明了什么呢，$a_1$ 可以流到 $b_1$ $x$ 流量，还可以流到 $b_2$ $x$ 流量，同时不影响 $a_1$ 与 $a_2$，$b_1$ 与 $b_2$ 之间的流量。因为是无向图，将 $a_1\to b_1$ 的流量反向，就可以得到 $b_1\to b_2$ $x$ 的流量。$b_1,b_2$ 之间的流就合法了。
• 同理 $a_1,a_2$ 之间的流也合法。
• 所以如果交换 $b_1,b_2$ 后仍满流，一定不存在这种问题。
  ​

【代码】

#include
#include
#include
#include
#define N 10005
#define M 1000005
#define inf (1ll<<31ll)-1
using namespace std;
char S[55][55];
int n,s,t,tot=1;
int v[M],w[M],nxt[M];
int f[N],d[N],first[N];
void add(int x,int y,int f)
{
	nxt[++tot]=first[x];
	first[x]=tot,v[tot]=y,w[tot]=f;
}
void Clear()
{
	tot=1;
	memset(first,0,sizeof(first));
}
bool bfs(int s)
{
	int x,y,i;
	memset(d,-1,sizeof(d));
	memcpy(f,first,sizeof(f));
	queue<int>q;q.push(s);d[s]=0;
	while(!q.empty())
	{
		x=q.front();q.pop();
		for(i=f[x];i;i=nxt[i])
		{
			y=v[i];
			if(w[i]&&d[y]==-1)
			{
				d[y]=d[x]+1;
				q.push(y);
			}
		}
	}
	return d[t]!=-1;
}
int dinic(int now,int flow)
{
	if(now==t)  return flow;
	int x,ans=0,delta;
	for(int &i=f[now];i;i=nxt[i])
	{
		x=v[i];
		if(d[x]==d[now]+1&&w[i])
		{
			delta=dinic(x,min(flow,w[i]));
			w[i]-=delta,w[i^1]+=delta;
			flow-=delta,ans+=delta;
			if(!flow)  return ans;
		}
	}
	return ans;
}
void addedge(int a1,int a2,int an,int b1,int b2,int bn)
{
	int i,j;Clear();
	add(s,a1,an),add(a1,s,0),add(s,b1,bn),add(b1,s,0);
	add(a2,t,an),add(t,a2,0),add(b2,t,bn),add(t,b2,0);
	for(i=0;i<n;++i)
	{
		for(j=0;j<n;++j)
		{
			if(S[i][j]=='O')  add(i,j,1),add(j,i,0);
			if(S[i][j]=='N')  add(i,j,inf),add(j,i,0);
		}
	}
}
int solve()
{
	int ans=0;
	while(bfs(s))
	  ans+=dinic(s,inf);
	return ans;
}
int main()
{
	int i,j,num1,num2;
	int a1,a2,an,b1,b2,bn;
	while(~scanf("%d",&n))
	{
		num1=num2=0,s=n+1,t=n+2;
		scanf("%d%d%d",&a1,&a2,&an);
		scanf("%d%d%d",&b1,&b2,&bn);
		for(i=0;i<n;++i)  scanf("%s",S[i]);
		addedge(a1,a2,an,b1,b2,bn),num1=solve();
		addedge(a1,a2,an,b2,b1,bn),num2=solve();
		puts(((num1==an+bn)&&(num2==an+bn))?"Yes":"No");
	}
	return 0;
}