mfcc总结，这个mel三角滤波器分组到底是如何起作用的呢？
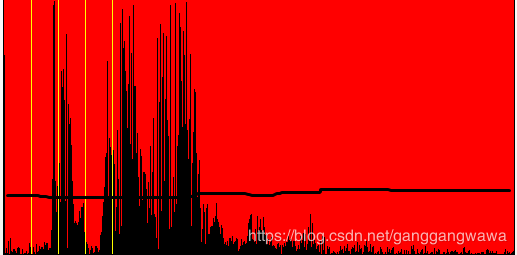
先看fft频谱图（这是4096字节取样fft计算，横轴频率是从0到512，后边意义不大，未取，纵轴是振幅），那些我随便画的蓝色线，你有什么联想？：
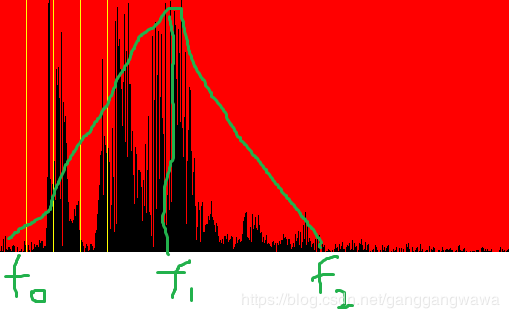
再看，这绿色线，是否有一种上升后，便逐渐式微的感觉，都是三角形的，这或许也是mel当初和绝大多数人看到的：
如果在振幅上加上一条限制的黑线（振幅门槛限制），黑色线以下很多频率就没有意义了，你看，有用的频率连一半（512/2=256）都占不到：
振幅的大小真是一个烦人的事情，变化很大，你不可能总是这么大的音量吧！取对数，这应该不是mel等人的专利，取对数产生了分贝的概念，他有一个好处，你立马可以看到，A=Math.Log10(10)=1，B=Math.Log10(100)=2，很明显A和B只相差1，而振幅相差很大，如果纵轴变为取对数，即分贝，那么，声音中的高频就会拔高，振幅大的低频就会降下来，振幅差别就变得没那么突兀了，但是fft纵轴没有取对数前，指示出来了你想要的那个区域，上面那个绿色的大三角，我们是否可以合并他呢？mel试了两个公式，来计算这个绿色三角形，假定f0=9，f1=16，f2=25，k属于【9,25】：
第1个公式，H（k）=（k-f0）/(f1-f0),k属于【9,16）;H（k）=（f2-k）/(f2-f1),k属于【16,25】,那么
|X(k)|^2*H(k)展开会是怎样的呢？（|X(k)|^2是傅里叶快速变换后的振幅能量）
|X(k)|^2*H(k)
=|X(9)|^2*H(9)+|X(10)|^2*H(10)+...+|X(16)|^2*H(16)+|X(17)|^2*H(17)+...+|X(24)|^2*H(24)+|X(25)|^2*H(25)
=0+|X(10)|^2*1/7+...+|X(15)|^2*6/7+|X(16)|^2*9/9+|X(17)|^2*8/9+...+|X(24)|^2*1/9+0
H(k)=0+1/7+...6/7+1+8/9+...+1/9+0=8！=1
第2个公式,H（k）=2*（k-f0）/[(f1-f0)*(f2-f0)],k属于【9,16）;H（k）=2*（f2-k）/[(f1-f0)*(f2-f0)],k属于【16,25】,那么|X(k)|^2*H(k)展开会是怎样的呢？（|X(k)|^2是傅里叶快速变换后的振幅能量）
计算分母[(f1-f0)*(f2-f0)]=7*16=112;
|X(k)|^2*H(k)
=|X(9)|^2*H(9)+|X(10)|^2*H(10)+...+|X(16)|^2*H(16)+|X(17)|^2*H(17)+...+|X(24)|^2*H(24)+|X(25)|^2*H(25)
=2*(0+|X(10)|^2*1+...+|X(15)|^2*6+|X(16)|^2*9+|X(17)|^2*8+...+|X(24)|^2*1+0)/112
H(k)=(2/112)*(1+...+6+9+...+1)=132/112=1.2,取整后H（k）=1
第一种方便，第二种复杂一些，似乎取整后H（k）=1看上去更顺眼，这两种方式，大家可能都会想到，但是，不用算，你就能猜到一个三角形的结果，所以，按第一幅图，主要突出划分三个三角形，特征好像比一个三角形好一些，继续试下去，这是否就是三角滤波器的来源呢？（很明显，图上f1处的振幅能量占比最高，然后向两边滑落，占比减少，直到零，界外无关，这很像一个三角形，三角形内相关，而且∑之后,只用一个值描述了这个三角形内的众多值,这明显是一种简并过滤行为）渐渐你也会发现前面分组要多一些，后面会少的多（人发声，主要在低频）。很显然，mel三角滤波方式弥补了fft取对数后带来的危害（100变2,10变1，没有了差别）。
但这不是最厉害的，mel发现了那个公式mel=2595*Math.Log10(1+f/700),还有人用mel=1125*Math.Log(1+f/700),这是我们望尘莫及的，这需要多少探索，经验，经历啊！在我国声学专家梁之安先生专著中（听觉感受和辨别的神经机制），好像都未发现这个公式，mel或许也是一个声学专家吧！
以上是mel分组的第一组测试，然后又试了第二组，均有取整后
H（k）=1，如果用归纳法，后面的组，应该也是这个结果，程序中我就不试了，有兴趣的可以一试。我的程序里抄的是第一种方式，现在看来，第二种方式可能要好一些。
顺眼是什么意思？似曾相识，却又想不起来的一种好感，取整后H（k）=1到底是什么？他有什么普遍意义呢？本想表达的意思，却突然忘记了，再一次回过头来看，灵感还在那里，他叫归一化，这个在图像处理里，或者现代科学里经常用到的不具美感的一个词，经常会忘记，那么，是否可以给他整一个集美貌与才华与一身的名字呢？有一种症状，叫‘脸盲’，路遇一人，我却常常记不住一些非常熟悉的名字，虽然理解足以到位（我知道你是谁），但就是喊不出这个名字（真尴尬！），归一化（不知是我的记忆有了问题，还是美感的问题）。
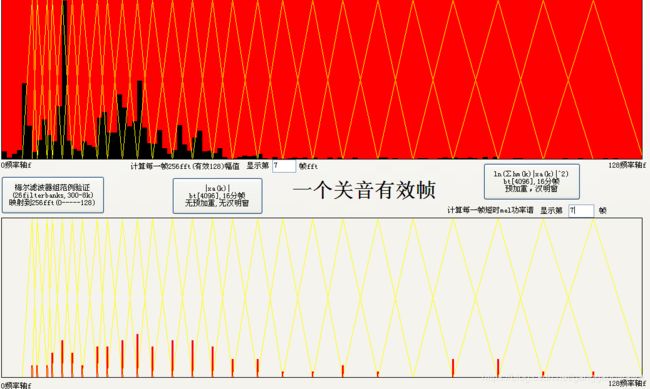
再看下图，是否豁然开朗了呢？以上就是第一个mel分组三角滤波器的全过程，他就是这样起作用的（简并出特征，使用了归一化思想）。
