【三角形最大路径和】递归、记忆化搜索、深度搜索（DFS打印所有路径、最大路径）、动态规划（DP）对比

参考链接，请参考原文，博主按照该文章顺了一遍，并加上自己的理解而已

下面所有的代码，如果不想提前新建nums[1000][1000]，可以使用双重list动态存储

深度优先搜索（DFS）：一般处理路径问题，二叉树的路径，二维数组的路径问题等等，一般需要递归，回溯
动态规划（DP）：一般处理最优化问题，最大值，最小值。

题目描述

有一个层数为n（n<=1000)的数字三角形。现有一只蚂蚁从顶层开始向下走，每走下一级，可向下或右下方向走。求走到底层后它所经过数字的总和的最大值。
【输入格式】
第一个整数为n,一下n行为各层的数字。
【输出格式】
一个整数，即最大值。
【输入样例 】
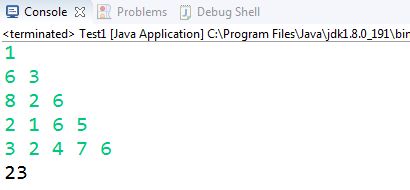
5
1
6 3
8 2 6
2 1 6 5
3 2 4 7 6
【输出样例】
23
【样例说明】
最大值=1+3+6+6+7=23

一、递归算法

思想：

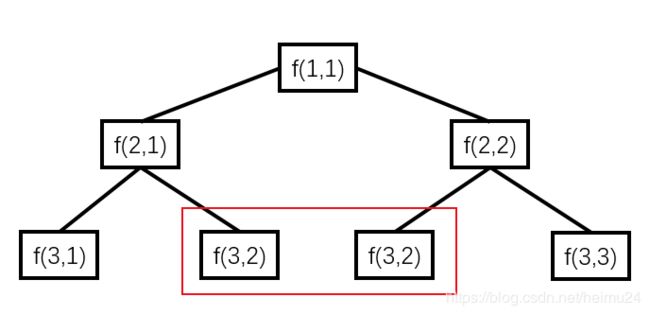
我们要知道某一点所能达到的最大值，这意味我们需要知道其下方或者右下所能达到的最大值（因为蚂蚁只能向下或者右下走），然后在此最大值的基础上再加上当前点的最大值即可，比如：f(1, 1)表示顶点(1, 1)出发所能达到的最大值，那么f(1, 1) = nums[1][1] + max(f(2, 1) + f(2, 2))，然后f(2, 1)和f(2, 2)又分别依赖其下方和右下方的最大值，具体看下图，然后按照这种自顶向下的计算顺序递归调用即可。

自顶向下：

就是从目标出发，我的目标是求f(1, 1)【注意看f的意义】，那么为了求f(1, 1)我需要求f(2,1)和f(2, 2)，如下图，依次类推。。知道最后一层（底层），可以直接得到f(5, 1)、f(4, 1)…f(5, 5)的值【递归结束条件】，然后再反向直到求得f(1, 1)的值，这就是递归。
存在问题：重复计算

import java.util.Scanner;
public class test1 {
	//静态全局变量
	static int[][] nums = new int[1001][1001];
	static int n;
	//递归函数
	public static int f(int x, int y) {
		if(x == n)
			return nums[x][y];
		return nums[x][y]+Math.max(f(x+1, y), f(x+1, y+1));
	}
	public static void main(String[] args) {
		Scanner sr = new Scanner(System.in);
		n = sr.nextInt();
		//三角形读入数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				nums[i][j] = sr.nextInt();
			}
		}
		System.out.println(f(1, 1));
	}
}

键盘输入及打印结果：

---

二、记忆化搜索算法

思想：

既然递归算法有重复值，那么我们就把计算的值保存起来，下次用的时候，如果存在就直接调用，不用在重复计算了。

import java.util.Scanner;
public class test1 {
	//静态全局变量
	static int[][] nums = new int[1001][1001];
	static int[][] did = new int[1001][1001];
	static int n;
	//递归函数
	public static int f(int i, int j) {
		if(i == n)
			return nums[i][j];
		//如果不为0，说明结果已经存储，直接拿来用，不用再进行下面的递归调用了
		if(did[i][j] != 0)
			return did[i][j];
		did[i][j] = nums[i][j] + Math.max(f(i+1, j), f(i+1, j+1));
		return did[i][j];
	}
	public static void main(String[] args) {
		Scanner sr = new Scanner(System.in);
		n = sr.nextInt();
		//三角形读入数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				nums[i][j] = sr.nextInt();
			}
		}
		System.out.println(f(1, 1));
	}
}

输入及打印结果

三、深度优先搜索（DFS）

思想：

就是一条道走到黑，比如给你一个起点，然后就沿着一条路一直走，前面走不通了，或者走完了，就返回上一下路口，再令选一条路走到黑。返回执行，直到所有路走完，这道题就是从顶点(1, 1)出发，把所有可能的路都走完，然后比较所有路径上和的最大值即可

import java.util.Scanner;
public class test1 {
	//静态全局变量
	static int[][] nums = new int[1001][1001];
	static int n;
	static int sum = 0;
	static int maxSum = Integer.MIN_VALUE;
	
	//递归函数
	public static void dfs(int i, int j) {
		//下面这条语句执行完，证明这个路径（节点）已经走过了
		//那么接下来判断是否走到头了，如果是，执行下面的if语句
		//如果没有，那么接着向下走（下方或者右下方）。递归
		sum += nums[i][j];
		//if(i == n)表示这条路走到头了，判断这条路的和是不是最大即可
		//递归结束
		if(i == n) {
			maxSum = Math.max(maxSum, sum);
			return;
		}
		for(int k = 0; k < 2; k++) {
			//两次递归，下方和右下方
			dfs(i+1, j+k);
			//回溯，比如你先向下走dfs(i+1, j)，执行完之后，应该烦返回当前节点
			//继续向当前节点的右下方dfs(i+1, j+1）走，问题的关键是你执行dfs(i+1, j)
			//的时候语句sum+=nums[i][j]是一定执行的【即加上了下方节点值】，所以当你返回到当前节点并继续向右下方
			//走的时候，一定要把下方节点的值减去，然后继续向右下走。
			sum -= nums[i+1][j+k];
		}
	}
	public static void main(String[] args) {
		Scanner sr = new Scanner(System.in);
		n = sr.nextInt();
		//三角形读入数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				nums[i][j] = sr.nextInt();
			}
		}
		dfs(1, 1);
		System.out.println(maxSum);
	}
}

输入及打印结果：

四、深度搜索（DFS）打印所有路径

思想：回溯的思想，先将当前节点添加到路径中，然后递归其下方或者右下的路径，注意的是，最后需要回溯一下，返回到当前节点的上一个节点，然后继续搜索。数据结构使用list。

import java.util.ArrayList;
import java.util.Scanner;
public class test1 {
	//静态全局变量
	static int[][] nums = new int[1001][1001];
	static int n;
	static int sum = 0;
	static int maxSum = Integer.MIN_VALUE;
	
	//递归函数
	static ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
	static ArrayList<Integer> list = new ArrayList<Integer>();
	public static void dfs(int i, int j) {
		//下面这条语句执行完，证明这个路径（节点）已经走过了
		//那么接下来判断是否走到头了，如果是，执行下面的if语句
		//如果没有，那么接着向下走（下方或者右下方）。递归
		list.add(nums[i][j]);
		sum += nums[i][j];
		//if(i == n)表示这条路走到头了，判断这条路的和是不是最大即可
		if(i == n) {
			maxSum = Math.max(maxSum, sum);
			res.add(new ArrayList<Integer>(list));
			//这点地方回溯是因为，if(i==n)那么就直接执行return，函数结束，最下面的回溯就无法执行
			//总之：不管当前节点是不是最后一个节点，回溯是必须的。最上面添加，最下面就要回溯。
			list.remove(list.size()-1);
			return;
		}
		for(int k = 0; k < 2; k++) {
			//两次递归，下方和右下方
			dfs(i+1, j+k);
			//回溯，比如你先向下走dfs(i+1, j)，执行完之后，应该烦返回当前节点
			//继续向当前节点的右下方dfs(i+1, j+1）走，问题的关键是你执行dfs(i+1, j)
			//的时候语句sum+=nums[i][j]是一定执行的【即加上了下方节点值】，所以当你返回到当前节点并继续向右下方
			//走的时候，一定要把下方节点的值减去，然后继续向右下走。
			sum -= nums[i+1][j+k];
		}
		//回溯一下
		list.remove(list.size()-1);
		
	}
	public static void main(String[] args) {
		Scanner sr = new Scanner(System.in);
		n = sr.nextInt();
		//三角形读入数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				nums[i][j] = sr.nextInt();
			}
		}
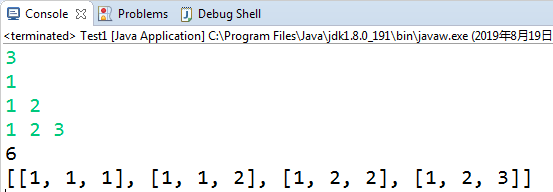
		dfs(1, 1);
		System.out.println(maxSum);
		System.out.println(res);
	}
}

输入及打印结果：

借用网友ouyangyanlan的回答：

• 使用list记录单次路径，使用双层list记录所有路径
• list.remove(list.size()-1) 这句话是模拟了栈回退。当前节点为底层节点或者已经访问过的情况下，回溯到上层节点。为什么？因为当前节点已经访问过了，那么说明该路径已经走过了，那么就需要返回上层节点寻找另外一条路径，很显然，当前节点不应该包含在另外的路径中，所以需要删除。
• listAll.add(new ArrayList(list)) 这个细节要注意，必须要重新生成一个对象实例，并使用list对其初始化赋值。不可以直接listAll.add(list)，因为list本质上是引用，在各次遍历中会直接改变它的值，最后的路径集合中前面的路径也会被后面的覆盖。再次强调这种做法是错误的。
• 这种思想和求取二叉树所有路径之类的问题一样。

五、深度搜索（DFS）：打印出和最大的路径

思想：在前面打印所有路径的基础上添加一个判断，如果当前路径大于max，就把当前路径加入到res中，那么最终res的最后一个路径就是和最大的路径。

import java.util.ArrayList;
import java.util.Scanner;
public class test1 {
	//静态全局变量
	static int[][] nums = new int[1001][1001];
	static int n;
	static int sum = 0;
	static int maxSum = Integer.MIN_VALUE;
	
	//递归函数
	static ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
	static ArrayList<Integer> list = new ArrayList<Integer>();
	public static void dfs(int i, int j) {
		//下面这条语句执行完，证明这个路径（节点）已经走过了
		//那么接下来判断是否走到头了，如果是，执行下面的if语句
		//如果没有，那么接着向下走（下方或者右下方）。递归
		list.add(nums[i][j]);
		sum += nums[i][j];
		//if(i == n)表示这条路走到头了，判断这条路的和是不是最大即可
		if(i == n) {
			//如果当前路径和较大，就存储，所以res的末尾的路径和最大
			if(sum > maxSum) {
				maxSum = sum;
				res.add(new ArrayList<Integer>(list));
			}
			list.remove(list.size()-1);
			return;
		}
		for(int k = 0; k < 2; k++) {
			//两次递归，下方和右下方
			dfs(i+1, j+k);
			//回溯，比如你先向下走dfs(i+1, j)，执行完之后，应该烦返回当前节点
			//继续向当前节点的右下方dfs(i+1, j+1）走，问题的关键是你执行dfs(i+1, j)
			//的时候语句sum+=nums[i][j]是一定执行的【即加上了下方节点值】，所以当你返回到当前节点并继续向右下方
			//走的时候，一定要把下方节点的值减去，然后继续向右下走。
			sum -= nums[i+1][j+k];
		}
		//模拟栈退回
		list.remove(list.size()-1);
		
	}
	public static void main(String[] args) {
		Scanner sr = new Scanner(System.in);
		n = sr.nextInt();
		//三角形读入数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				nums[i][j] = sr.nextInt();
			}
		}
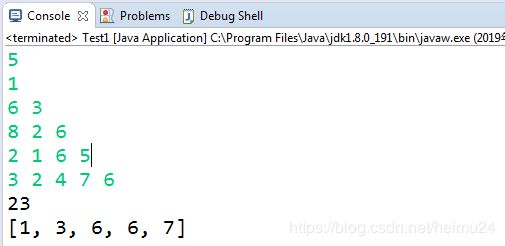
		dfs(1, 1);
		System.out.println(maxSum);
		int length = res.size()-1;
		System.out.println(res.get(length));
	}
}

输入及打印结果

六、动态规划（dp）：求解最优化（最大值、最小值）问题：

思想：

动态规划一般用于解决最优化问题，且大问题可以分解为若干个小问题，这些小问题之间存在重叠部分，所以一般是从上往下分析问题，从下往上解决问题。我们总是解决最小问题开始，并把最优问题的最优解存储下来（一维或者二维数组）（避免重复计算），并把子问题组合起来解决大的问题。

• 自定向下分析
• 定义dp[i][j]表示从（i,j）出发到底层的最大和，所以我们的目标dp[1][1]
• 从(1,1)出发，那么接下来向(2,1)走呢还是(2, 2)走呢？这就需要比较(2, 1)到底层的最大值和(2,2)到底层的最大值。即dp[1][1] = max(dp[2][1], dp[2][2]) + nums[1][1]，所以将大问题转化为两个字问题，。。然后依次向下类推。。
• 自低向上解决问题
• 初始化最小问题的解，也就是底层的解：dp[5][1],dp[5][2]…dp[5][5]就是其值本身
• 然后从倒数第二层开始，状态转移方程：dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + nums[i][j]
• 返回最大问题的值dp[1][1]，这就是我们的目标值。

import java.util.Scanner;
public class test1 {
	//静态全局变量
	static int[][] nums = new int[1001][1001];
	static int[][] dp = new int[1001][1001];
	static int n;
	public static int dp() {
		for(int i = n; i >= 1; i--) {
			for(int j = 1; j <= i; j++) {
				//初始化底层状态
				if(i == n) {
					dp[i][j] = nums[i][j];
				}
				//状态转移方程
				else {
					dp[i][j] = Math.max(dp[i+1][j], dp[i+1][j+1]) + nums[i][j];
				}
			}
		}
		
		return dp[1][1];
	}
	public static void main(String[] args) {
		Scanner sr = new Scanner(System.in);
		n = sr.nextInt();
		//三角形读入数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				nums[i][j] = sr.nextInt();
			}
		}
		int res = dp();
		System.out.println(res);
	}
}

输入及打印结果：

七：动态规划（dp）：打印最大和的路径

思想：就是取出二维dp数组中，每一行dp值最大的索引，然后对应到原数组nums中，即得最大和的路径

import java.util.Scanner;
public class test1 {
	//静态全局变量
	static int[][] nums = new int[1001][1001];
	static int[][] dp = new int[1001][1001];
	static int n;
	public static int dp() {
		for(int i = n; i >= 1; i--) {
			for(int j = 1; j <= i; j++) {
				//初始化底层状态
				if(i == n) {
					dp[i][j] = nums[i][j];
				}
				//状态转移方程
				else {
					dp[i][j] = Math.max(dp[i+1][j], dp[i+1][j+1]) + nums[i][j];
				}
			}
		}
		
		//获得最大和的路径
		int temp;
		for(int i = 1; i <= n; i++) {
			int maxdp = dp[i][1];
			temp = nums[i][1];
			for(int j = 1; j <= i; j++) {
				if(dp[i][j] > maxdp){
					maxdp = dp[i][j];
					temp = nums[i][j];
				}
			}
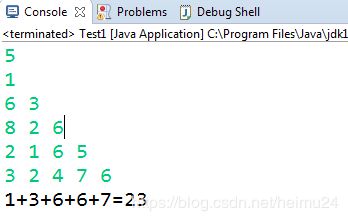
			System.out.print(temp);
			if(i != n)
				System.out.print("+");
			else
				System.out.print("=");
		}
		return dp[1][1];
	}
	public static void main(String[] args) {
		Scanner sr = new Scanner(System.in);
		n = sr.nextInt();
		//三角形读入数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				nums[i][j] = sr.nextInt();
			}
		}
		int res = dp();
		System.out.println(res);
	}
}

输入及打印结果