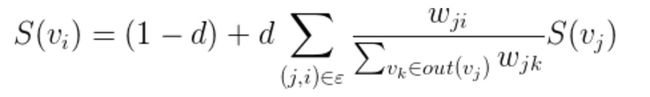NLP入门-Task3 特征选择

关键词

关键词简介

关键词是文本里面跟这篇文档意义最相关的一些词，是最能够反映出文本主题或者意思的词语。关键词在文本聚类、分类、自动摘要等领域中有着重要的作用。比如在聚类时将关键词相似的几篇文档看成一个团簇，可以大大提高聚类算法的收敛速度；从某天所有的新闻中提取出这些新闻的关键词，就可以大致了解那天发生了什么事情；或者将某段时间内几个人的微博拼成一篇长文本，然后抽取关键词就可以知道主要在讨论什么话题。

关键词抽取

关键词抽取方法大致有两种：
第一种是关键词分配，就是有一个给定的关键词库，然后新来一篇文档，从词库里面找出几个词语作为这篇文档的关键词；
第二种是关键词抽取，就是新来一篇文档，从文档中抽取一些词语作为这篇文档的关键词；
目前大多数领域无关的关键词抽取算法（领域无关算法的意思就是无论什么主题或者领域的文本都可以抽取关键词的算法）和它对应的库都是基于后者的。从逻辑上说，后者比前者在实际使用中更有意义。

从算法的角度来看，关键词抽取算法主要有两类：
有监督学习算法，将关键词抽取过程视为二分类问题，先抽取出候选词，然后对于每个候选词划定标签，要么是关键词，要么不是关键词，然后训练关键词抽取分类器。当新来一篇文档时，抽取出所有的候选词，然后利用训练好的关键词抽取分类器，对各个候选词进行分类，最终将标签为关键词的候选词作为关键词；
无监督学习算法，先抽取出候选词，然后对各个候选词进行打分，然后输出topK个分值最高的候选词作为关键词。根据打分的策略不同，有不同的算法，例如TF-IDF，TextRank等算法；
jieba分词系统中实现了两种关键词抽取算法，分别是基于TF-IDF关键词抽取算法和基于TextRank关键词抽取算法，两类算法均是无监督学习的算法。

TF-IDF算法分析

在信息检索理论中，TF-IDF是Term Frequency - Inverse Document Frequency的简写。TF-IDF是一种数值统计，用于反映一个词对于语料中某篇文档的重要性。在信息检索和文本挖掘领域，它经常用于因子加权。

TF-IDF的主要思想就是：如果某个词在一篇文档中出现的频率高，也即TF高；并且在语料库中其他文档中很少出现，即DF低，也即IDF高，则认为这个词具有很好的类别区分能力。

TF-IDF在实际中主要是将二者相乘，也即TF * IDF，TF为词频（Term Frequency），表示词t在文档d中出现的频率；IDF为反文档频率（Inverse Document Frequency），表示语料库中包含词t的文档的数目的倒数。

TF=count(t)/count(di)，公式中count(t)表示文档di中包含词t的个数；
count(di)表示文档di的词的总数；

IDF=num(corpus)/num(t)+1，公式中num(corpus)表示语料库corpus中文档的总数；num(t)表示语料库corpus中包含t的文档的数目；

应用到关键词抽取：

1. 预处理，首先进行分词和词性标注，将满足指定词性的词作为候选词；
2. 分别计算每个词的TF-IDF值；
3. 根据每个词的TF-IDF值降序排列，并输出指定个数的词汇作为可能的关键词；

TextRank算法分析

类似于PageRank的思想，将文本中的语法单元视作图中的节点，如果两个语法单元存在一定语法关系（例如共现），则这两个语法单元在图中就会有一条边相互连接，通过一定的迭代次数，最终不同的结点会有不同的权重，权重高的语法单元可以作为关键词。

结点的权重不仅依赖于它的入度结点，还依赖于这些入度结点的权重，入度结点越多，入度结点的权重越大，说明这个结点的权重越高；

TextRank迭代计算公式为：

结点i的权重取决于结点i的邻居结点中i-j这条边的权重 / j的所有出度的边的权重 * 结点j的权重（S(vj)），将这些邻居结点计算的权重相加，再乘上一定的阻尼系数，就是结点i的权重；阻尼系数 d 一般取0.85；

算法通用流程：

1. 标识文本单元，并将其作为顶点加入到图中；
2. 标识文本单元之间的关系，使用这些关系作为图中顶点之间的边，边可以是有向或者无向，加权或者无权；
3. 基于上述公式，迭代直至收敛；
4. 按照顶点的分数降序排列；

应用到关键短语抽取：

1. 预处理，首先进行分词和词性标注，将单个word作为结点添加到图中；
2. 设置语法过滤器，将通过语法过滤器的词汇添加到图中；出现在一个窗口中的词汇之间相互形成一条边；
3. 基于上述公式，迭代直至收敛；一般迭代20-30次，迭代阈值设置为0.0001；
4. 根据顶点的分数降序排列，并输出指定个数的词汇作为可能的关键词；
5. 后处理，如果两个词汇在文本中前后连接，那么就将这两个词汇连接在一起，作为关键短语；

计算TF-IDF的值

import math
from collections import Counter
corpus = [
    'this is the first document',
    'this is the second second document',
    'and the third one',
    'is this the first document'
]
#分词
word_list = []
for i in range(len(corpus)):
    word_list.append(corpus[i].split(' '))
print(word_list)
#统计词频
countlist = []
for i in range(len(word_list)):
    count = Counter(word_list[i])
    countlist.append(count)
print(countlist)
#计算TF值
def tf(word, count):
    return count[word] / sum(count.values())
#统计的是含有该单词的句子数
def n_containing(word, count_list):
    return sum(1 for count in count_list if word in count)
#len(count_list)是指句子的总数，n_containing(word, count_list)是指含有该单词的句子总数，加1是为了防止分母为0
def idf(word, count_list):
    return math.log(len(count_list) / (1 + n_containing(word, count_list)))
# 将tf和idf相乘
def tfidf(word, count, count_list):
    return tf(word, count) * idf(word, count_list)
for i, count in enumerate(countlist):
    print("Top words in document {}".format(i + 1))
    scores = {word: tfidf(word, count, countlist) for word in count}
    sorted_words = sorted(scores.items(), key=lambda x: x[1], reverse=True)
    for word, score in sorted_words[:]:
        print("\tWord: {}, TF-IDF: {}".format(word, round(score, 5)))

互信息

互信息

两个离散随机变量 X 和 Y 的互信息定义为：

其中 p(x,y) 是 X 和 Y 的联合概率分布函数，而p(x)和p(y)分别是 X 和 Y 的边缘概率分布函数。
在连续随机变量的情形下，求和被替换成了二重定积分：

其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数，而p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。

互信息量I(xi;yj)在联合概率空间P(XY)中的统计平均值。 平均互信息I(X;Y)克服了互信息量I(xi;yj)的随机性,成为一个确定的量。如果对数以 2 为基底，互信息的单位是bit。

互信息度量 X 和 Y 共享的信息：知道这两个变量其中一个，度量对另一个不确定度减少的程度。例如，如果 X 和 Y 相互独立，则知道 X 不对 Y 提供任何信息，反之亦然，所以它们的互信息为零。在另一个极端，如果 X 是 Y 的一个确定性函数，且 Y 也是 X 的一个确定性函数，那么传递的所有信息被 X 和 Y 共享：知道 X 决定 Y 的值，反之亦然。因此，在此情形互信息与 Y（或 X）单独包含的不确定度相同，称作 Y（或 X）的熵。而且，这个互信息与 X 的熵和 Y 的熵相同。（这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。）

互信息是 X 和 Y 联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。于是互信息以下面方式度量依赖性：I(X; Y) = 0 当且仅当 X 和 Y 为独立随机变量。从一个方向很容易看出：当 X 和 Y 独立时，p(x,y) = p(x) p(y)，I(X;Y) =0.

点互信息

点互信息PMI（Pointwise Mutual Information）这个指标来衡量两个事物之间的相关性（比如两个词）。

其原理很简单，公式如下：

在概率论中，如果x跟y不相关，则二者相关性就小，点互信息为0。用后面的式子可能更好理解，在y出现的情况下x出现的条件概率除以x本身出现的概率，自然就表示x跟y的相关程度。 这里的log来自于信息论的理论，可以简单理解为，当对取log之后就将一个概率转换为了信息量（要再乘以-1将其变为正数），以2为底时可以简单理解为用多少个bits可以表示这个变量。

点互信息PMI其实就是从信息论里面的互信息这个概念里面衍生出来的。其衡量的是两个随机变量之间的相关性，即一个随机变量中包含的关于另一个随机变量的信息量。所谓的随机变量，即随机试验结果的量的表示，可以简单理解为按照一个概率分布进行取值的变量，比如随机抽查的一个人的身高就是一个随机变量。可以看出，互信息其实就是对X和Y的所有可能的取值情况的点互信息PMI的加权和，而点互信息只是对其中两个点进行相关性判断。

特征筛选

from sklearn import metrics as mr
mr.mutual_info_score(label,x)

来计算x和label的互信息，label、x为list或array。

参考博文
结巴分词5–关键词抽取
使用不同的方法计算TF-IDF值
互信息（Mutual Information）的介绍
sklearn：点互信息和互信息