两轮差速移动机器人运动分析、建模和控制

文中每个模型、算法和仿真的程序都将在仿真结果前给出对应的下载链接。

1 运动学分析建模

运动特性为两轮差速驱动，其底部后方两个同构驱动轮的转动为其提供动力，前方的随动轮起支撑作用并不推动其运动，如图1两轮差速驱动示意图所示。

定义其左右驱动轮的中心分别为$W_l$和$W_r$，且车体坐标系中这两点在惯性坐标系下移动的线速度为$v_l$和$v_r$，理想情况下即为左右轮转动时做圆周运动的线速度。该值可以通过电机驱动接口输出的角转速${\varphi }_l$，${\varphi }_r$和驱动轮半径$r$求得，即：
$$v_l=r\cdot {\varphi }_l$$
令两驱动轮中心连线的中点为机器的基点$C$，$C$点在大地坐标系$XOY$下坐标为$(x,y)$，机器的瞬时线速度为$v_c$，瞬时角速度${\omega }_c$，姿态角$\theta$即为$v_c$与$X$轴夹角。此时，机器位姿信息可用矢量$P=[x,y,\theta {]}^T$表示。机器人瞬时线速度为$v_c$可以表示为：
$$v_c=\frac{v_r+v_l}{2}$$
令左右轮间距为$l$，且机器瞬时旋转中心（ICR）为$O_c$，转动半径即为$C$到$O_c$的距离$R$。机器在做同轴（轴为左右轮到ICR连线）圆周（圆心为ICR）运动时，左右轮及基点所处位置在该圆周运动中的角速度相同${\omega }_l={\omega }_r={\omega }_c$，到旋转中心的半径不同，有$l=\frac{v_r}{{\omega }_r}-\frac{v_l}{{\omega }_l}$。则机器的瞬时角速度${\omega }_c$可以表示为：
$${\omega }_c=\frac{v_r-v_l}{l}$$
联立两式，利用$v_r$和$v_l$求出机器转动半径：
$$R=\frac{v_c}{{\omega }_c}=\frac{l}{2}\frac{v_r+v_l}{v_r-v_l}$$

1.1 三种运动状态分析

差速驱动方式，即V1和V2间存在的速度差关系决定了其具备不同的三种运动状态，如图所示：

• 当$v_l>v_r$时，机器做圆弧运动；
• 当$v_l=v_r$时，机器做直线运动；
• 当$v_l=-v_r$时，机器以左右轮中心点做原地旋转。

1.2 函数模型

通过上述两节的运动分析，在驱动轮与地面接触运动为纯滚动无滑动情况下，机器的运动学模型可以表示为：
$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{cc}cos\theta & 0\\ sin\theta & 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}\frac{1}{2}& \frac{1}{2}\\ \frac{1}{l}& -\frac{1}{l}\end{array}\right]\left[\begin{array}{c}{v}_r\\ v_l\end{array}\right]$$

1.3 仿真验证

MATLAB仿真程序免积分下载链接。

1.3.1 直线验证

位移变化：

姿态角变化曲线：

1.3.2 曲线验证

位移变化：
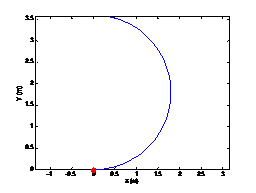姿态角变化曲线：
（机器人坐标系服从右手定则，其顺时旋转针姿态角减少，逆时针旋转姿态角增加）

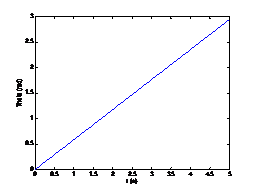
1.3.3 旋转验证

位移变化：
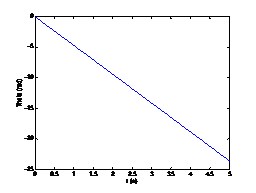
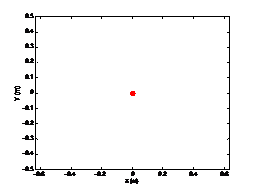姿态角变化曲线：
（机器人坐标系服从右手定则，其顺时旋转针姿态角减少，逆时针旋转姿态角增加）

2 运动控制

运动控制的被控对象是所分析的两轮差速移动机器人；直观的控制量是上述建模中所述的左右轮转速，为了更一般的描述车体的运动，控制量选车体线速度$v$与角速度$\omega$，左右轮转速可由模型反求取。

2.1 点到点

控制机器人由当前点移动到指定目标点，其核心是令机器人在控制器作用下（以一定合适的方式）持续地朝向目标点运动。其控制系统框图为：

2.1.1 任意姿态到达目标点

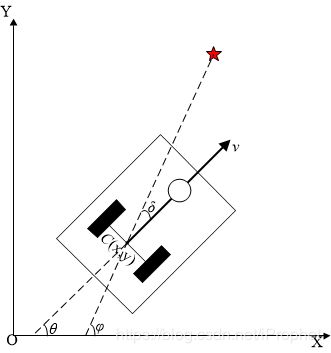
设机器人实时位姿为$[x_t,y_t,{\theta }_t]$，目标位置为$[x_G,y_G,{\theta }_G]$，易求出机器与目标点间实时的距离差$d_{err}=\sqrt{(x_G-x_t{)}^2+(y_G-y_t{)}^2}$与角度差${\theta }_{err}=\tan (\frac{y_G-y_t}{x_G-x_t})-{\theta }_t$（即图中$\delta =\phi -\theta$），如下图所示。
一种简单通用的控制器，PID控制器可以构成运动控制器。其设计方法是：简单地，运动控制器由两个并联的PID控制器组成：

• 一个PID控制器，输入为距离差$d_{err}$输出为线速度$v$，即距离决定速度。距离远速度大，距离近速度小。【多说一句，这里要注意的是速度的连续性，（如起步时距离远，线速度由0跳变为较大值，且距离无穷远速度无穷大）所以需要将PID输出先限幅再平滑(即限幅$\Vert v_{pidout}\Vert \le v_{max}$，平滑$\Vert v_{t-1}-v_{pidout}\Vert \le \sigma$)，最后输出$v_t=v_{pidout}$】
• 另一个PID控制器，输入为距离差${\theta }_{err}$输出为角速度$\omega$，即偏角误差决定转速。正偏左转，负偏右转；偏多转快，偏少转慢。【多说一句，这里要注意的是角度表示方式带来的过界问题，即当求出的${\theta }_{err}$大于或小于$\pi$（如$\phi =\frac{3}{4}\pi$，$\theta =-\frac{3}{4}\pi$）时，要将其归一化到$(-\pi ,\pi ]$。即 ${\theta }_{err}$大于$\pi$减$2\pi$；小于等于$-\pi$，加$2\pi$ 】

使用上述公式求出线速度$v_c$、角速度${\omega }_c$后，再解算为左右轮转速交给机器执行。控制器会控制机器人持续朝向目标移动，当其距离目标小于一定值，即移动到以目标为圆心，$\tau$为半径（目标半径）的圆内$d_{err}\le \tau$时，判定机器人到达目标位置，完成运动控制过程。
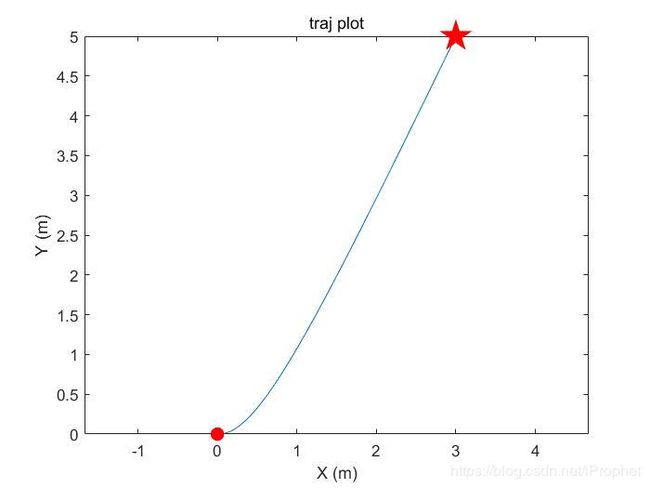
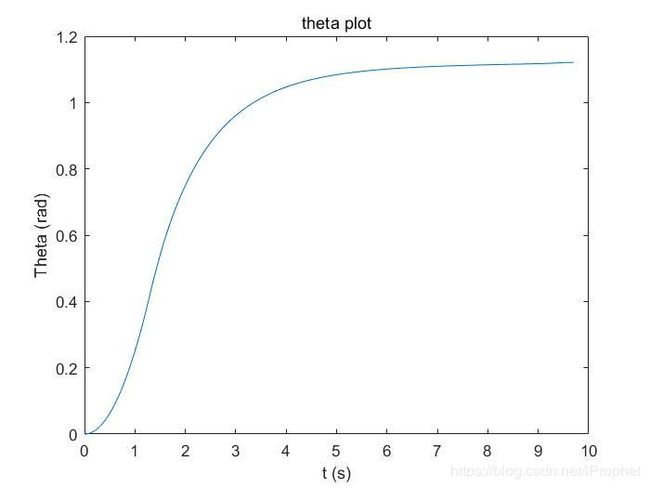
该控制系统简单易实现，这里是仿真的下载链接，控制效果如图所示。

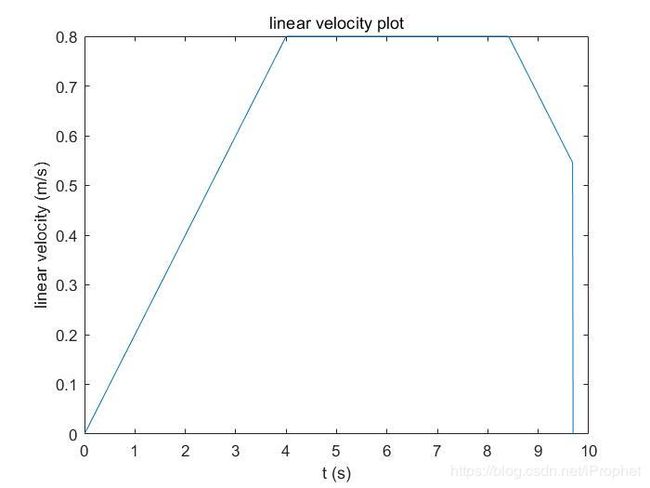
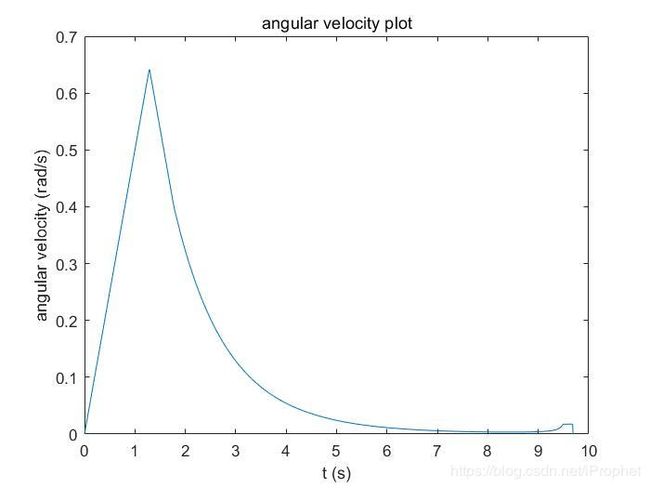
2.1.1 固定姿态到达目标点

上述点到点的运动控制只要求到达目标点，并没有其他约束条件，虽然在实际应用中往往会有许多约束，但是其确是一切运动控制的基石。
在某些具体应用中，如泊车parking，对接docking等往往需要机器人以某个固定的姿态到达某一具体位置。

2.2 路径跟踪

路径跟踪（巡迹/沿线）是指机器人在已知地图上跟随已规划好路径进行运动的过程。路径跟踪的算法有很多，较为常用的如Pure pursuit，Stanley(针对Ackerman模型)，MPC等等。考虑到通用性，这里主要介绍Pure pursuit控制算法。

2.2.1 Pure pursuit 纯跟踪

路径是由什么组成的？很显然，路径是由无数个离散的目标点组成的。通过遍历这些目标点，是不是就可以完成路径的跟随？那么，这些目标点的遍历过程是不是可以通过上面介绍的点到点运动控制来完成？路径上离散的目标点间距那么小，又怎么实现控制？pure pursuit纯跟踪算法应运而生。
Pure pursuit是最基础的路径跟踪算法了，它的核心思想是：通过航向控制，不断地将机器人从当前位置移动到机器人前面的某个前瞻点。pure pursuit算法将根据机器人的当前位置计算出此时路径上对应的前瞻点，并控制其朝向前瞻点移动，不断循环上述过程（机器动，前瞻动）直到到达路径的最后一个点。通俗一点的说，就是机器人在不断地追逐它前面的一个点。
对于pure pursuit纯跟踪算法来说，前瞻点的选取至关重要！前瞻点是根据机器人实时位置通过前瞻距离向前搜素而来。机器人实时位置和前瞻点如图所示，注意实际路径与规划路径不匹配。

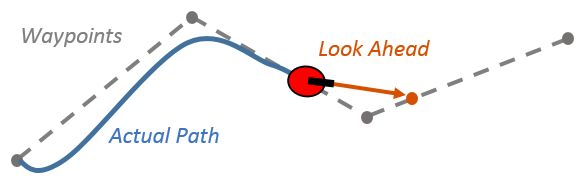
前瞻距离决定了跟踪路径的方式，前瞻距离较小，机器将更快速的靠向规划路径，从而实际路径将更贴合规划路径，但是也会伴随着实际路径的震荡；反之，较大的前瞻距离，可以减少沿路径的振荡，但也会导致拐角附近的曲率较大。同时，不同的线速度和角速度也会影响机器对规划路径的响应，在控制过程中也应该考虑到这一点。
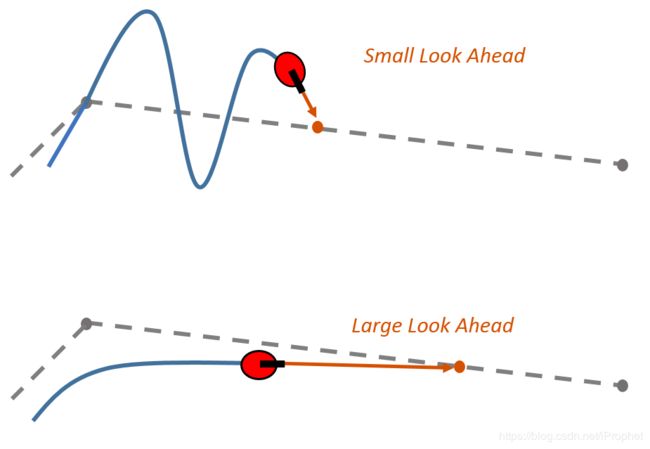纯追踪算法有几个局限性需要注意：

• 纯追踪算法不能完全遵循规划路径。必须调整参数以优化性能，使得机器随时间收敛到路径上。
• 纯追踪算法不能使机器在某一点上保持稳定。可以用目标位置的距离阈值来将其停在目标附近。

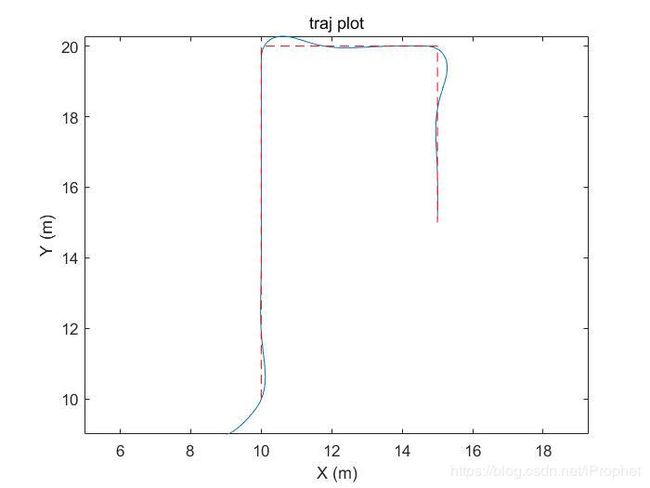
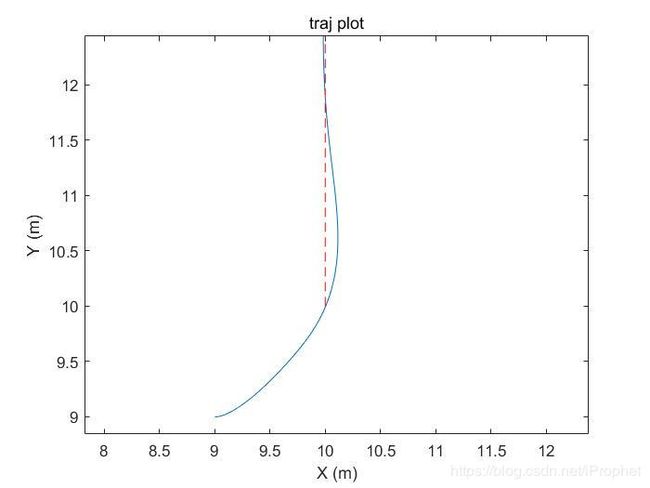
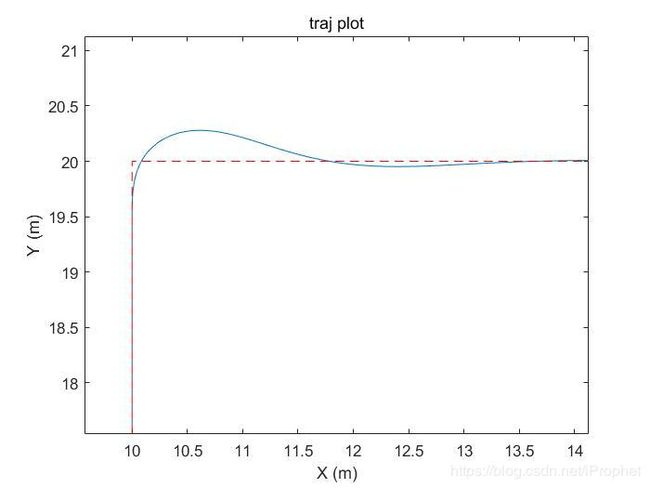
算法的整体和细节效果如下，红色虚线为规划轨迹，蓝色实线为实际路径。位置不会一直贴合路径，但是随时间一定会收敛到路径上。

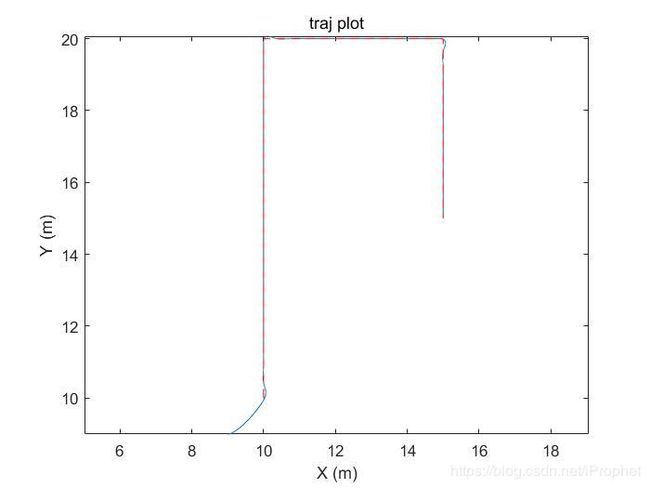
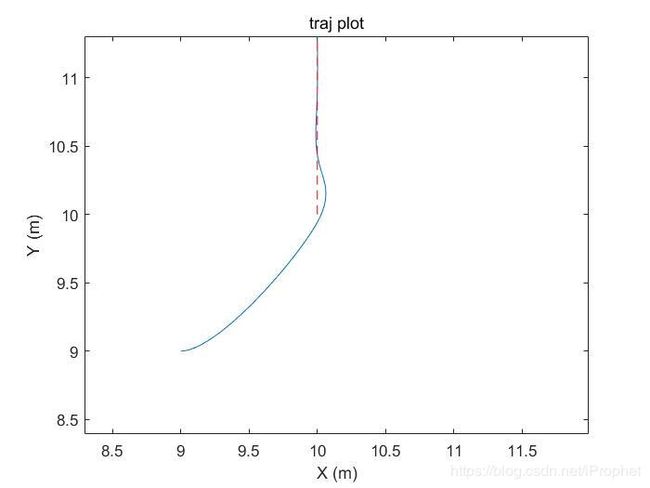
将前瞻距离加大，贴合路径的速度降低收敛变慢：