fcm算法的MATLAB实现

fcm算法

分析：

1.算法中包含的参数：
a.模糊因子expo(expo>1)
b.最大迭代次数max_t
c.迭代终止条件ε

2.算法中包含的过程：
a.目标函数
b.欧式距离
c.隶属矩阵
d.聚类中心
e.迭代过程

还有  不要忘记！！初始化！！

3.实现代码过程中需要写成子函数的部分：
a.初始化函数initfcm() （主要实现隶属度矩阵的初始化）
b.一次聚类过程stepfcm()（包含目标函数，隶属矩阵的计算等等）
c.距离函数distfcm()
d.画图函数plotfcm()

---

代码实现：

· 函数定义–左边是输出参数，右边是函数名以及输入参数

主函数：

function[center, U, obj_fcn] = fcm_final(data,c,options)
% 输入：
% data 数据集 n行m列，n为样本数据数，m为数据的特征数
% c 聚类中心的个数
%options(1): 隶属度矩阵U的指数expo，>1(缺省值: 2.0)
%options(2): 最大迭代次数max_t(缺省值: 100)
%options(3): 隶属度最小变化量e,迭代终止条件(缺省值: 1e-5)
%options(4): 每次迭代是否输出信息标志(缺省值: 1)
% 输出：
% U 隶属度矩阵
% center 聚类中心
% obj_fcn 目标函数

% 判断输入参数的个数只能是2个或者3个
if nargin ~= 2 && nargin ~= 3
    error('Too many or too few input argument! ');
end
data_n = size(data, 1);% 求数据的行，即样本个数
data_m = size(data, 2);% 求数据的列，即特征个数

% 默认操作参数
default_options = [2; 100; 1e-5; 1];

% 如果输入参数个数为2，调用默认的options参数
if nargin == 2,
    options = default_options;
else % 分析有options做参数的情况：
     % 用户在输入options参数时需注意，如果options参数的个数少于4个，则未输入参数的对应位置用nan来代替，这样可以保证未输入参数采用的是默认值，否则可能会出现前面参数占用后面参数的值的情况，从而影响聚类效果。
    if length(options) < 4,
        temp = default_options;
        temp(1:length(options)) = options;
        options = temp;
    end
    % 返回options中值为NaN的索引位置
    nan_index = find(isnan(options) == 1);
    % 将default_options中对应位置的参数值付给options中值为NaN的值
    options(nan_index) = default_options(nan_index);
    if options(1) <= 1,% 模糊因子是大于1的数
        error('The exponent should be greater than 1 !');
    end

end

% 将options中的分量分别复制给四个变量
expo = options(1);%模糊因子m
max_t = options(2);% 最大迭代次数
e = options(3);%迭代终止条件
display = options(4);%输出信息

% 目标函数初始化
obj_fcn = zeros(max_t, 1);
U = initfcm(c, data_n);
% 初始化模糊分配矩阵，使U满足列上相加值为1

% 主要循环
for i = 1 : max_t
    % 在第k步循环中改变聚类中心center和隶属矩阵U
    [U, center, obj_fcn(i)] = stepfcm(data, U, c, expo);
    if display,
        fprintf('FCM:Iteration count = %d, obj_fcn = %f\n',i,obj_fcn(i));
        plotfcm(data,center,U,obj_fcn);
    end

    %迭代终止条件的判断
    if i > 1,
        if abs(obj_fcn(i) - obj_fcn(i-1)) < e,
            break;
        end
    end

end

% 实际迭代次数
iter_n = i;
% 清除迭代次数之后的值
obj_fcn(iter_n + 1 : max_t) = [];
end


% 初始化fcm的隶属度函数矩阵，满足列向量之和为1

子函数：

1.初始化函数initfcm()

% U--> c * n(c行n列) ，c为聚类数, n为样本数
%% 初始化隶属矩阵时需要已知矩阵的行和列，因此输入应该为该矩阵的行和列

% 输入: c, data_n
% data_n  数据集data所含的样本数
% c       这组数据的聚类数
% 输出：U（初始化之后的隶属矩阵）

function[U] = initfcm(c, data_n)

% 初始化隶属矩阵U：rand函数可产生在(0, 1)之间均匀分布的随机数组成的数组。
U = rand(c, data_n);    

%% 注意：隶属矩阵在初始化时需满足某数据j对各个聚类中心i(1%% sum(U)是指对矩阵U进行纵向相加，即求每一列的和，结果是一个1行n列的矩阵。(sum函数后面参数不指定或指定为1时均表示列相加)。

col_sum = sum(U);

U = U./col_sum(ones(c,1), : );

% col_sum(ones(cluster_n, 1),:)等效于ones(clusters_n,1)*col_sum
% 上述目的是将col_sum扩展成与U（c,data_n）大小相同的矩阵，然后进行对应元素的点除，使隶属矩阵列项和为1。

%% 这里必须要多说一句，因为我一开始死活不理解这一句怎么能使得隶属矩阵列项和为1。建议可以用一组简单的数据做尝试，之后你会发现，它就是一道简单的数学题！！

end

2.一次聚类过程stepfcm()

% 一次聚类包含的过程：
% % （1）计算聚类中心，（2）目标函数，（3）距离函数，（4）计算新的隶属矩阵

% 输入：data,U,c,expo(模糊因子)
% 输出：U_new（新的隶属矩阵），center（聚类中心），obj_fcn（目标函数）

function[U_new, center, obj_fcn] = stepfcm(data, U, c, expo)

% 对隶属矩阵进行指数运算（加上模糊因子）
mf = U.^expo; % 隶属矩阵模糊化
% 相当于一次性将所有聚类中心作为一个矩阵计算出来
center = mf*data./((ones(size(data,2),1)*sum(mf'))');
dist = distfcm(center, data); % 计算距离矩阵
obj_fcn = sum(sum(dist.^2 * mf)); % 计算目标函数
temp = dist.^(-2/(expo-1));
U_new = temp./(ones(c,1)*sum(temp)); % 计算新的隶属矩阵
end

3.距离函数distfcm()

% 输入：data, center
% 输出：out

function out = disfcm(center,data)
out = zeros(size(center, 1), size(data, 1)); % 对c行n列的距离输出矩阵进行置零
% 循环，每循环一次计算所有样本点到该聚类中心的距离
for k = 1:size(center, 1)
    out(k,:) = sqrt(sum(((data - ones(size(data,1),1)*center(k,:)).^2)',1));
end
end

4.画图函数plotfcm()

% 输入：data, center, U, obj_fcn
% 对fcmdata.dat（MATLAB自带的聚类数据集，有两个类）进行聚类

function plotfcm(data,center,U,obj_fcn)

figure(1)
subplot(2,1,1);
plot(U(1,:),'-b');
title('隶属度矩阵值')
ylabel('第一类')
subplot(2,1,2);
plot(U(2,:),'-r');
ylabel('第二类')
xlabel('样本数')

figure(2)
grid on
plot(obj_fcn);
title('目标函数变化值');
xlabel('迭代次数')
ylabel('目标函数值')

figure(3)
title('聚类图像');
plot(data(:,1),data(:,2),'*r');
maxU = max(U);
index1 = find(U(1,:)==maxU);
index2 = find(U(2,:)==maxU);
plot(data(index1,1),data(index1,2),'*g');
hold on
plot(data(index2,1),data(index2,2),'*r');
plot(center(1,1),center(1,2),'oy','Markersize',5,'linewidth',3)
plot(center(2,1),center(2,2),'ob','Markersize',5,'linewidth',3)
hold off;
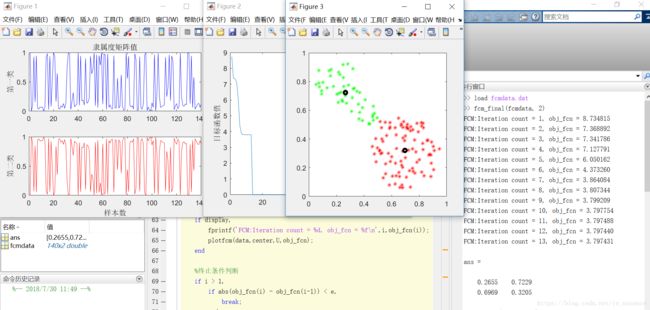
end

聚类结果

收获心得

%% 由于具有4个特征值的鸢尾花数据集是四维的，无法在图像中展示，可采用两两比对的方式展现。
%% 代码中的隶属度矩阵啊聚类中心啊目标函数啊等等这些表示实际上都是将算法中的数学计算式转化成矩阵问题，要注意理解。