说说算法题的那些事儿(1)
1.墓地雕塑(Graveyard, NEERC 2006, LA 3708)
在一个周长为10000的圆上等距分布着n个雕塑。现在又有m个新雕塑加入(位置可以随意放),希望所有n+m个雕塑在圆周上均匀分布。这就需要移动其中一些原有的雕塑。要求n个雕塑移动的总距离尽量小。
【输入格式】
输入包含若干组数据。每组数据仅一行,包含两个整数n和m(2≤n≤1 000,1≤m ≤1 000),即原始的雕塑数量和新加的雕塑数量。输入结束标志为文件结束符(EOF)。
【输出格式】
输入仅一行,为最小总距离,精确到10-4。
【样例输入】
2 1
2 3
3 1
10 10
【样例输出】
1666.6667
1000.0
1666.6667
0.0
【样例解释】
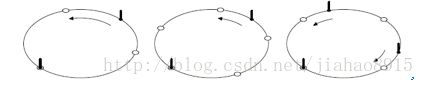
前3个样例如图所示。白色空心点表示等距点,黑色线段表示已有雕塑。
【分析】
请仔细看看样例。3个样例具有一个共同的特点:有一个雕塑没有移动。如果该特点在所有情况下都成立,则所有雕塑的最终位置(称为“目标点”)实际上已经确定。为了简单起见,我们把没动的那个雕塑作为坐标原点,其他雕塑按照逆时针顺序标上到原点的距离标号,如图所示。
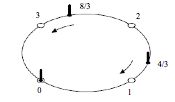
注意,这里的距离并不是真实距离,而是按比例缩小以后的距离。接下来,我们把每个雕塑移动到离它最近的位置。如果没有两个雕像移到相同的位置,那么这样的移动一定是最优的。代码如下。
#include注意在代码中,坐标为pos的雕塑移动到的目标位置是floor(pos+0.5),也就是pos四舍五入后的结果。这就是坐标缩小的好处。
这个代码很神奇地通过了测试,但其实这个算法有两个小小的“漏洞”:首先,我们不知道是不是一定有一个雕塑没有移动;其次,我们不知道会不会有两个雕塑会移动到相同的位置。如果你对证明不感兴趣,或者已经想到了证明,再或者迫不及待地想阅读更有趣的问题,请直接跳到下一个例题。否则,请继续阅读。
第一个“漏洞”的修补需要证明我们的猜想。证明思路在例题3中我们已经展示过了,具体的细节留给读者思考。
第二个“漏洞”有两种修补方法。第一种方法相对较容易实施:由于题目中规定了n,
m≤1 000,我们只需要在程序里加入一个功能——记录每座雕塑移到的目标位置,就可以用程序判断是否会出现“人多坑少”的情况。这段程序的编写留给读者,这里可以明确地告诉大家:这样的情况确实不会出现。这样,即使无法从理论上证明,也可以确保在题目规定的范围内,我们的算法是严密的。
第二种方法就是直接证明。在我们的程序中,当坐标系缩放之后,坐标为x的雕塑被移到了x四舍五入后的位置。如果有两个坐标分别为x和y的雕塑被移到了同一个位置,说明x和y四舍五入后的结果相同,换句话说,即x和y“很接近”。至于有多接近呢?差距最大的情况不外乎类似于x=0.5, y=1.499 999…。即便是这样的情况,y-x仍然小于1(尽管很接近1),但这是不可能的,因为新增雕塑之后,相邻雕塑的距离才等于1,之前的雕塑数目更少,距离应当更大才对。
例题5 蚂蚁(Piotr’s Ants, UVa 10881)
一根长度为L厘米的木棍上有n只蚂蚁,每只蚂蚁要么朝左爬,要么朝右爬,速度为1厘米/秒。当两只蚂蚁相撞时,二者同时掉头(掉头时间忽略不计)。给出每只蚂蚁的初始位置和朝向,计算T秒之后每只蚂蚁的位置。
【输入格式】
输入的第一行为数据组数。每组数据的第一行为3个正整数L, T, n(0≤n≤10 000);以下n行每行描述一只蚂蚁的初始位置,其中,整数x为蚂蚁距离木棍左端的距离(单位:厘米),字母表示初始朝向(L表示朝左,R表示朝右)。
【输出格式】
对于每组数据,输出n行,按输入顺序输出每只蚂蚁的位置和朝向(Turning表示正在碰撞)。在第T秒之前已经掉下木棍的蚂蚁(正好爬到木棍边缘的不算)输出Fell off。
【样例输入】
2
10 1 4
1 R
5 R
3 L
10 R
10 2 3
4 R
5 L
8 R
【样例输出】
Case #1:
2 Turning
6 R
2 Turning
Fell off
Case #2:
3 L
6 R
10 R
【分析】
假设你在远处观察这些蚂蚁的运动,会看到什么?一群密密麻麻的小黑点在移动。由于黑点太小,所以当蚂蚁因碰撞而掉头时,看上去和两个点“对穿而过”没有任何区别,换句话说,如果把蚂蚁看成是没有区别的小点,那么只需独立计算出每只蚂蚁在T时刻的位置即可。比如,有3只蚂蚁,蚂蚁1=(1, R),蚂蚁2= (3, L),蚂蚁3=(4, L),则两秒钟之后,3只蚂蚁分别为(3,R)、(1,L)和(2,L)。
注意,虽然从整体上讲,“掉头”等价于“对穿而过”,但对于每只蚂蚁而言并不是这样。蚂蚁1的初始状态为(1,R),因此一定有一只蚂蚁在两秒钟之后处于(3,R)的状态,但这只蚂蚁却不一定是蚂蚁1。换句话说,我们需要搞清楚目标状态中“谁是谁”。
也许读者已经发现了其中的奥妙:所有蚂蚁的相对顺序是保持不变的,因此把所有目标位置从小到大排序,则从左到右的每个位置对应于初始状态下从左到右的每只蚂蚁。由于原题中蚂蚁不一定按照从左到右的顺序输入,还需要预处理计算出输入中的第i只蚂蚁的序号order[i]。完整代码如下。
#include例题6 立方体成像(Image Is Everything, World Finals 2004, LA 2995)
有一个n×n×n立方体,其中一些单位立方体已经缺失(剩下部分不一定连通)。每个单位立方体重量为1克,且被涂上单一的颜色(即6个面的颜色相同)。给出前、左、后、右、顶、底6个视图,你的任务是判断这个物体剩下的最大重量。
【输入格式】
输入包含多组数据。每组数据的第一行为一个整数n(1≤n≤10);以下n行每行从左到右依次为前、左、后、右、顶、底6个视图,每个视图占n列,相邻视图中间以一个空格隔开。顶视图的下边界对应于前视图的上边界;底视图的上边界对应于前视图的下边界。在视图中,大写字母表示颜色(不同字母表示不同颜色),句号(.)表示该位置可以看穿(即没有任何立方体)。输入结束标志为n=0。
【输出格式】
对于每组数据,输出一行,即物体的最大重量(单位:克)。
【样例输入】
3
.R. YYR .Y. RYY .Y. .R.
GRB YGR BYG RBY GYB GRB
.R. YRR .Y. RRY .R. .Y.
2
ZZ ZZ ZZ ZZ ZZ ZZ
ZZ ZZ ZZ ZZ ZZ ZZ
0
【样例输出】
Maximum weight: 11 gram(s)
Maximum weight: 8 gram(s)
【分析】
这个问题看上去有点棘手,不过仍然可以找到突破口。比如,能“看穿”的位置所对应的所有单位立方体一定都不存在。再比如,如果前视图的右上角颜色A和顶视图的右下角颜色B不同,那么对应的格子一定不存在。如图所示。
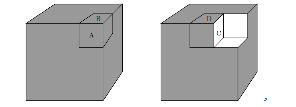
在删除这个立方体之后,我们可能会有新发现:C和D的颜色不同。这样,我们又能删除一个新的立方体,并暴露出新的表面。当无法继续删除的时候,剩下的立方体就是重量最大的物体。
可能有读者会对上述算法心存疑惑。解释如下:首先不难证明第一次删除是必要的(即被删除的那个立方体不可能存在于任意可行解中),因为只要不删除这个立方体,对应两个视图的“矛盾”将一直存在;接下来,我们用数学归纳法,假设算法的前k次删除都是必要的,那么第k+1次删除是否也是必要的呢?由刚才的推理,我们不能通过继续删除立方体来消除矛盾,而由归纳假设,已经删除的立方体也不能恢复,因此矛盾无法消除。
下面给出完整代码。
#include程序用了一个get函数来表示第k个视图中,第i行j列、深度为len的单位立方体在原立方体中的坐标(x,y,z),另外还使用了宏REP精简程序。尽管用宏缩短代码在很多时候会降低程序可读性,但本题却不会(如果到处都是for循环,反而容易令人犯晕)。