编译原理:LL(1)文法-构造预测分析表
LL(1)文法-构造预测分析表
复习笔记
LL(1)文法分析(自上而下)是语法分析中比较重要的一个方法,其中比较重要的环节是构造预测分析表。
当然,在构造预测分析表之前,需要掌握两个集合的求法:FIRST集合和FOLLOW集合。
注意:下文的测试用例中使用的文法如下:
E→TE’
E’→+TE’|ε
T→FT’
T’→*FT’|ε
F→(E)|i
FIRST集合的求法
- 方法步骤如下:
1、X∈VT (终结符号集合)
FIRST(X)={X}(即:终结符号的FIRST集仍然是其本身)。
2、X∈VN(非终结符号集合)
(1)若X→a…, 则 a 加入FIRST(X);若有X→ε,则ε加入 FIRST(X)(a是X可以推出的首个终结符号)。
(2)若有X→Y…, 且Y∈VN ,则FIRST(Y)中非ε元素全部加入FIRST(X);
(3)若有X→Y1Y2Y3…YK ,且Yi∈VN ,ε∈FIRST(Yj) ,则FIRST(Yi)中非ε元素加入FIRST(X);若所有的FIRST(Yj)都含有ε,则ε加入FIRST(X)。
- 例解:
求非终结符号的First集:
First(E)={(,i}
First(E’)={+,ε}
First(T)={(,i}
First(T’)={*,ε}
First(F)={(,i}
FOLLOW集合的求法
我个人觉得FOLLOW集合比FIRST集合的求解难度较大,并且也涉及到FIRST集合的运算。
- FOLLOW的求解步骤
(1)对于文法开始符号S, 将#(作用:结束标记)加入FOLLOW(S)。
(2)若有A→ αBβ,则FIRST(β)-{ε}加入FOLLOW(B)。
(3)若有A→αB, 或A→αBβ且ε ∈ FIRST(β),则将FOLLOW(A) 加入FOLLOW(B)中。
NOTE
(1)FOLLOW集合中没有 ε;
(2)以上步骤中的α,β是任意的文法符号串。
- 例解
非终结符的Follow集:
Follow(E)={),#}
Follow(E’)={),#}
Follow(T)={+,),#}
Follow(T’)={+,),#}
Follow(F)={*,+,),#}
构造预测分析表
预测分析程序由分析栈(倒序),分析表和分析程序三部分组成,其中分析表的构成与文法有关,是比较重要的。其要求的文法是LL(1)文法,所以先补充一下LL(1)文法的知识。
LL(1)文法
- LL(1)文法的条件
(1)文法不含左递归
(2)对文法中每一个非终结符A的各个产生式的FIRST集合两两不相交。
(3)对文法中每一个非终结符A,若存在某个FIRST集合包含ε,则: First(A)∩ Follow(A)=∅。
以上三个条件可以用来判断一个文法是不是LL(1)文法。一般情况下,我们见到的文法不全是不含有左递归的文法,但是我们可以通过一定的方式消除左递归,继而寻求方法构造一个LL(1)文法。
- 消除左递归
2、消除间接左递归
将间接左递归转为直接左递归进行消除
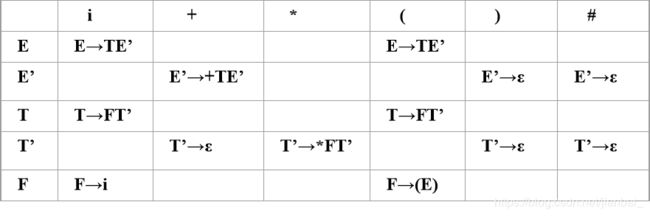
构造预测分析表
一般来说, 预测分析表可以用矩阵M表示:
(1)矩阵的行表示非终结符号
(2)列表示终结符号和#(结束符号)
(3)矩阵元素M(U,a)表示非终结符号U+输入符号a时,向下推导所应该采取的产生式。