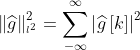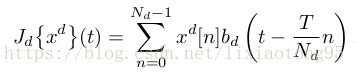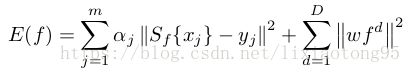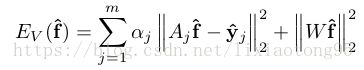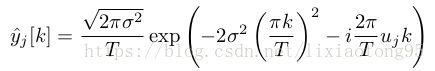C-COT -- 超越相关滤波：学习连续卷积算子(Continuous Convolution Operators)

 

在目标跟踪算法中，ECO算法表现很优秀，是基于C-COT跟踪算法的改进（Martin 林雪平大学）。因此学习C-COT是理解和改

进ECO算法的基础和关键。

 

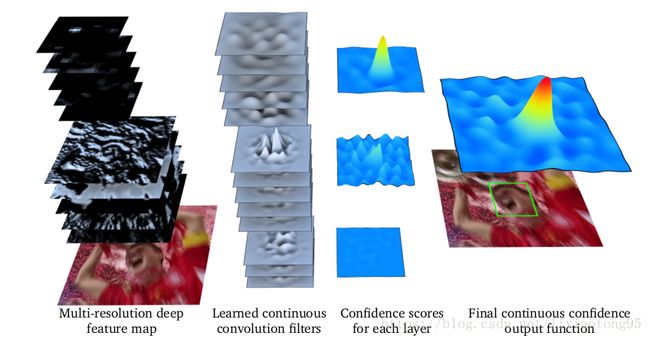
一、C-COT算法的整体核心原理如下图所示：

 

                       多分辨率深度特征图         习得的连续卷积滤波器      每层置信度              最终的连续置信度输出函数

 

　　图中是可视化的应用于多分辨率深度特征映射的连续卷积算子。 第一列是输入的 RGB patch 和预训练好的深层网络的第

一个卷积层和最后一个卷积层的特征图。第二列是框架学习到的连续卷积滤波器的可视化。每一层连续卷积输出的结果（第三

列）被组合成目标（绿色框）的最终连续置信度函数（第四列）。

　　文章提出一种用于学习连续空间域中的卷积算子的新公式，采用训练样本的隐式插值模型。通过学习一组卷积滤波器来产

生目标的连续域置信度图。 这可以在联合学习公式中实现多分辨率特征映射的完美融合。

　　除了多分辨率融合之外，连续域学习公式还可以实现精确的亚像素定位。 这一点通过用亚像素精确连续置信度图标记训练

样本来实现。因此这种构造也适用于精确特征点跟踪。

　　此外，这样的学习的方法具有辨别性，并且不需要在图像上明确插值实现亚像素精度。且已在流行的MPI Sintel数据上进行

了广泛的特征点跟踪实验，证明了C-COT的准确性和鲁棒性。

 

二、相关介绍和工作

   　 判别相关滤波器（DCF）表现让人满意。这些方法利用滑动窗口的循环相关属性训练回归器。最初，DCF方法仅限于单通

道特道。 后来DCF框架扩展到多通道特征图。多通道DCF可以将高维特征（如HOG和CN Color Names）纳入其中。除了包含

多通道特征之外，DCF框架最近也通过加入尺度估计(Scale Estimation)，非线性核函数(Non-linear kernels)，长期记忆(long-

term memory)，和减轻循环卷积的周期性影响等方法进行了显著改进。

　　随着深度CNN的出现，网络的全连接层被普遍用于图像表示。最近，最后一层卷积层被证明对图像分类更有利。另一方

面，与深层相比，第一层（浅层）的卷积层更适合视觉跟踪。深卷积层具有判别性，并具有高级视觉信息。相反，浅层包含高

空间分辨率的低层特征，有利于定位。独立DCF跟踪器的分层集合中采用了多个卷积层。与之相反，C-COT框架中提出了一种

新型的的连续方程，在这个联合学习框架中融合具有不同空间分辨率的多个卷积层。

　　而特征点跟踪不同于目标跟踪，它是准确评估特殊关键点运动的任务。大多数特征点跟踪方法都来自经典的KLT跟踪器。

KLT跟踪器是一种生成方法，原理是最小化两个图像块之间差异的平方和。在过去的几十年里，花费了大量精力来改进KLT跟踪

器。相比之下，C-COT是一种基于判别式学习的特征点跟踪方法。我们的方法：我们的主要贡献是用于学习连续空间域中的区

分卷积算子的理论框架。

 

C-COT与传统的DCF框架相比具有两大优势：

(１)允许多分辨率特征图的自然整合，如卷积层或多分辨率HOG和颜色特征的组合。特别适用于对象跟踪，检测和动作识别。

(２)连续公式能够实现准确的亚像素定位，这在许多特征点跟踪问题中至关重要。

 

三、学习连续卷积算子（Continuous Convolution Operators）

本节提出学习连续卷积算子的理论框架。 其中的公式是通用的，可用于有监督学习任务，如视觉跟踪和检测。

(１) 首先，在一维空间定义学习公式和方法。

复值函数 在空间 中，以 （ 0 ）为周期且勒贝格平方可积。 是一个希尔伯特空间，在此空间上

定义内积算子 ，则对于函数 ，有傅里叶变换对：

傅里叶级数定义为：,

同时满足一下性质：  , 其中 , 

                               ,   ， 其中

(２) 然后，给出转化至连续域的插值算子公式。

学习的目标是训练一个基于训练样本 的连续卷积算子。每个训练样本 包含 个从同一块 image patch 中提取的特征通道（feature channels）每个特征通道 中的采样数(分辨率)为 ,  表示在离散空间变量中的索引。

由此，样本空间即可表示为：。

接下来，用一个内插算子 把特征离散空间变换到一个连续区间

整个内插算子   由内插函数   的各个平移形式叠加来构造， 代表每个平移后的函数的加权值。

(３)接下来定义连续卷积算子学习公式。

线性卷积算子 将样本映射成一个定义在连续区间中的目标置信函数

，它是目标在图像的位置处的置信分数，我们通过寻找图片区域中的最大置信分数来定位目

标 由一系列卷积滤波器 参数化，是针对特征通道 的连续滤波器。

最后将所有特征通道中全部滤波器的卷积响应加起来得到最后的置信函数。

注：寻找最大置信度（目标定位）方法－标准牛顿法（第二步）。第一步采用网格搜索进行粗略的初始化估计。

(４) 定义最小化泛函

滤波器 是在给定的 个训练样本对下，最小化泛函 得到(相当于最小化loss函数)

控制每个训练样本的影响力(权重)，是正则化项，C-COT的正则化策略与SRDCF算法中相同。

采用这种正则化策略可以通过控制滤波器的空间长度在任意大的区域上学习，是关于空间位置的权重矩阵，通常背景区域的

值大，目标区域的值小。 P.S.限制条件-- 含有有限个非零傅里叶级数 。

(５)最小化方法思路：在傅里叶域最小化

由数学推导，根据傅里叶变换的帕塞瓦尔定理（能量守恒定理）可将最小化 的公式等价于 相对于每个滤波器

的傅里叶系数 的最小化，如下式：

出于实际考虑，我们的滤波器组要是有限数量的，因此在有限维子空间上获得的最小化。换句话说，我们相对于系数

　最小化。设置，以使得 通道存储的滤波器系数的数目与训练样本的空间分辨率.

进一步数学推导后，等价于下式的最小平方问题：

这个最小平方问题可以通过求解一下正规方程获得－－共轭梯度法迭代求解：

（６）期望置信度和插值函数，即   和  的定义方式。　

定义 为以 为中心的高斯函数的周期重复，  是目标的估计位置。

函数   的构造基于三次插值核函数 ,    被设置为，即 经缩放和平移后的周期重复。

的傅里叶级数表示为。

将上述过程推广到高维空间（二维即可表示图像），进行图像域的运算。

 

四、目标跟踪框架（Tracking Frameworks）　

(１)目标定位

步骤一：网格搜索，在空间离散点，处估计得分函数，找到最大值，作为迭代优化的初始值。

步骤二：把上一步中获得的最大值作为傅里叶级数展开的初始值，进行5次标准牛顿法迭代。

(２)跟踪框架

1、从预训练好的深度网络中提取出多分辨率特征图；

2、每帧中提取单个(一个)训练样本，从以目标位置为中心的图像区域提取样本，并将区域大小设置为目标框区域的倍(可以调节)。设置相应的权重为，学习率参数，然后将权重归一化，即;

3、采用多尺度搜索策略(5个尺度 和 相对比例因子1.02)

4、最大化网格搜索后，进行 5 次牛顿迭代；

5、求解正规方程以训练滤波器,采用共轭梯度法进行迭代，在第一帧中，使用100次迭代找到滤波器系数 的初始估计，随后

的帧中，用当前的滤波器初始化CG(共轭梯度)，每帧五次迭代就足够。（参数可调，并且在之后的ECO中运用跳帧更新策略）

 

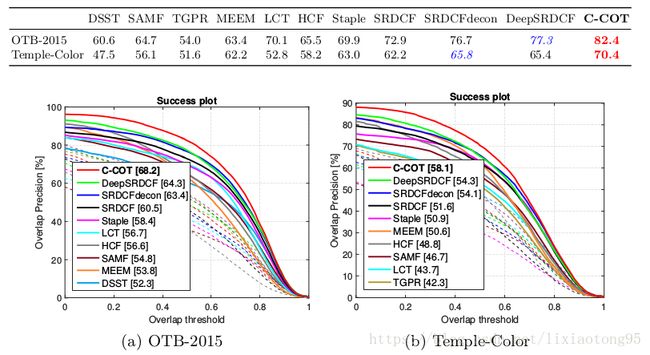
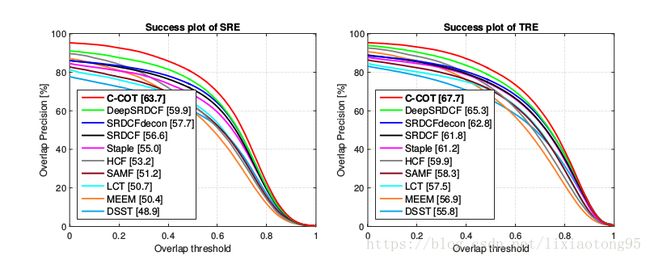
五、实验（略，详见论文）

六、总结

贡献：

１、提出了一个通用框架来学习连续空间域中的区分卷积算子。验证了这个框架有两个功能：对象跟踪和特征点跟踪。

２、公式可以集成多分辨率特征地图，能够精确地进行亚像素定位。

３、三个跟踪基准数据集上的实验表明，本文方法显着提高了实时跟踪的准确度和鲁棒性。

有待改进：

１、没有使用任何视频数据学习特定的深度特征表示，可以进一步改善跟踪框架的性能。

２、另一个研究方向是将基于运动的深度特征整合到跟踪框架中。