分治法之归并排序三种实现方法(递归、非递归和自然合并排序)
1. 递归实现归并排序
基本思想:
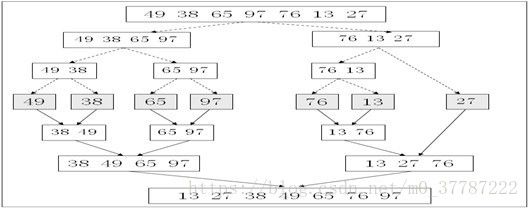
将待排元素分成大小大致相同的2个子集,分别对2个子集合进行排序,最终将排好序的子集合合并 就会得到一个排好序的集合 即为所求
设归并排序的当前区间是R[low..high],分治法的三个步骤是:
① 分解:将当前区间一分为二,即求分裂点
② 求解:递归地对两个子区间R[low..mid]和R[mid+1..high] 进行归并排序;
③ 组合:将已排序的两个子区间R[low..mid]和R[mid+1..high] 归并为一个有序的区间R[low..high]。
递归的终结条件:子区间长度为1(一个记录自然有序)。
/*
数组a[]为待排序数组,数组b[]用来存放已排好序的数
left、right分别为待排序数组最左端和最右端的下标
mid为数组下标的中点
*/
(算法导论版是借助两个数组,这个例子是借助了一个数组)
#include
#include
using namespace std;
#define maxn 100
int num[maxn];
//将数组b[]中的数复制到数组a[]中
template<class Type>
void Copy(Type a[],Type b[],int left,int right)
{
for(int i=left;i<=right;i++)
a[i]=b[i];
}
//将已排好序的数组合并到数组b[]中
template<class Type>
void Merge(Type a[],Type b[],int left,int mid,int right)
{
int i=left;
int j=mid+1;
int k=left;
while(i<=mid && j<=right)
//i的取值范围为 [left,mid], j的取值范围为 [mid+1,right]
{
if(a[i]//取左右两边数组中较小的元素放入数组b中,最后得到的数组b即为有序
b[k++]=a[i++];
else
b[k++]=a[j++];
}
if(i>mid) //说明右边的数组的元素个数多
for(int z=j;z<=right;z++)
b[k++]=a[z];
else
for(int z=i;i<=mid;i++)
b[k++]=a[z];
}
//将待排序集合一分为二,直至待排序集合只剩下一个元素为止,
//然后不断合并两个排好序的数组段
template<class Type>
void MergeSort(Type a[],int left,int right)
{
Type *b=new Type [maxn];
if(left//控制待排序数组中至少有两个元素,一个元素时为有序
{
int i=(left+right)/2; //取数组中点,将数组尽量均等划分
MergeSort(a,left,i); //将左半段进行递归排序
MergeSort(a,i+1,right); //将右半段进行递归排序
Merge(a,b,left,i,right); //合并到数组b
Copy(a,b,left,right); //复制到数组a
}
delete[] b;
}
int main()
{
int n;
while(cin>>n)
{
for(int i=0;icin>>num[i];
MergeSort(num,0,n-1);
for(int i=0;icout<return 0;
}
/*
7
49 38 65 97 76 13 27
*/ 2. 非递归实现归并排序
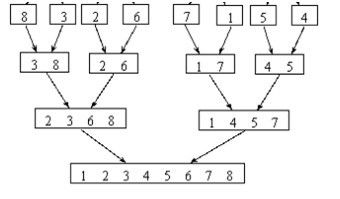
基本思想:
将数组中的相邻元素两两配对。用Merge()函数将他们排序,构成n/2组长度为2的排序好的子数组段,然后再将他们合并成长度为4的子数组段,如此继续下去,直至整个数组排好序
#include
#include
using namespace std;
#define maxn 100
int num[maxn];
template<class Type>
void Merge(Type a[],Type b[],int left,int mid,int right)
{
int i=left;
int j=mid+1;
int k=left;
while(i<=mid && j<=right)
{
if(a[i]else
b[k++]=a[j++];
}
if(i>mid)
for(int z=j;z<=right;z++)
b[k++]=a[z];
else
for(int z=i;z<=mid;z++)
b[k++]=a[z];
}
//合并大小为s的相邻子数组
template<class Type>
void MergePass(Type x[],Type y[],int s,int n)
{
int i=0;
while(i+2*s-11,i+2*s-1);
//合并大小为s的相邻2段子数组
i+=2*s;
}
if(i+s//剩下的元素个数m满足:s<= m <2*s
Merge(x,y,i,i+s-1,n-1);
else
//剩下的元素个数m满足:m
for(int j=i;j<=n-1;j++)
y[j]=x[j];
}
template<class Type>
void MergeSort(Type c[],int n)
{
Type *d=new Type [n];
int s=1;
while(s//合并到数组d
s+=s;
//就像图中有序的两个合并为一个
MergePass(d,c,s,n); //合并到数组c
s+=s;
}
delete[] b;
}
int main()
{
int n;
while(cin>>n)
{
for(int i=0;icin>>num[i];
MergeSort(num,n);
for(int i=0;icout<return 0;
}
/*
8
8 3 2 6 7 1 5 4
7
49 38 65 97 76 13 27
5
49 38 65 97 76
*/ 3. 自然合并排序
1) 基本思想:
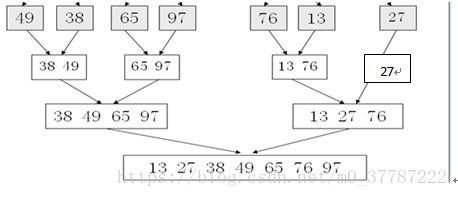
对于初始给定的数组a,通常存在多个长度大于1的已排好序的子数组段。因此用一次对a的线性扫描就可以找出所有这些排好序的子数组段,然后将相邻的排好序的子数组段两两合并
2) 样例:
若数组a中元素为{4,8,3,7,1,5,6,2},则自然排好序的子数组段有{4,8},{3,7},{1,5,6},{2},经一次合并后得到2个合并后的子数组段{3,4,7,8}和{1,2,5,6},继续合并相邻排好序的子数组段,直至整个数组已排好序,最终结果{1,2,3,4,5,6,7,8}
3) 代码实现
#include
#include
#include
#includeif(begin>x[i])//如果begin大于了之后的元素,证明有新的有序序列
sl[k++]=i;//有序子串数量增加,i是有序子串的开始位置
begin=x[i];//每次改变begin,可以用于后面有序序列的判断
}
sl[k++]=n;//无论如何,最后一个有序子串一定是数组最后元素的位置
return k;
}
template<class Type>
void MergeSort(Type a[],int n)
{
Type *b=new Type [n];
int sNum=MergePass(a,n); //sNum = 有序子串的个数 +1
cout <<"sNum:"<< sNum<while(sNum!=2)//如果sNum为2证明这个数组已经有序了,不需要在进行转换
{
for(int i=0;i2)//因为是两两合并,所以每次递增2
{
Merge(a,b,sl[i],sl[i+1]-1,sl[i+2]-1);
//对sNUm个子串进行两两合并
//因为除了第一数组元素,k++之后的元素的数值都大了1
}
sNum=MergePass(a,n); //求出经上次合并后的数组中有序子串的个数
//cout <<"sNum:"<< sNum<
}
delete[] b;
}
int main()
{
int n;
while(cin>>n)
{
memset(num,0,sizeof(num));
memset(sl,0,sizeof(sl));
for(int i=0;icin >>num[i];
MergeSort(num,n);
for(int i=0;icout<return 0;
}
/*
7
49 38 65 97 76 13 27
7
13 27 49 38 65 97 76
*/ 原文地址http://www.360doc.com/content/16/0928/16/10408243_594414491.shtml