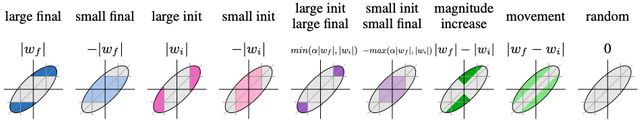深度学习中的模型修剪

本文讨论了深度学习环境中的修剪技术。

本在本文中，我们将介绍深度学习背景下的模型修剪机制。 模型修剪是一种丢弃那些不代表模型性能的权重的艺术。 精心修剪的网络会使其压缩版本更好，并且它们通常变得适合设备上的部署。

本文的内容分为以下几节：

• 函数和神经网络中的“非重要性”概念
• 修剪训练好的神经网络
• 代码片段和不同模型之间的性能比较
• 现代修剪技术
• 最后的想法和结论

（我们将讨论的代码段将基于TensorFlow模型优化工具包）

函数中的“不重要”概念

神经网络是函数近似器。 我们训练他们来学习可构成输入数据点的基础表示的函数。 神经网络的权重和偏差称为其（可学习的）参数。 通常，权重被称为正在学习的函数的系数。

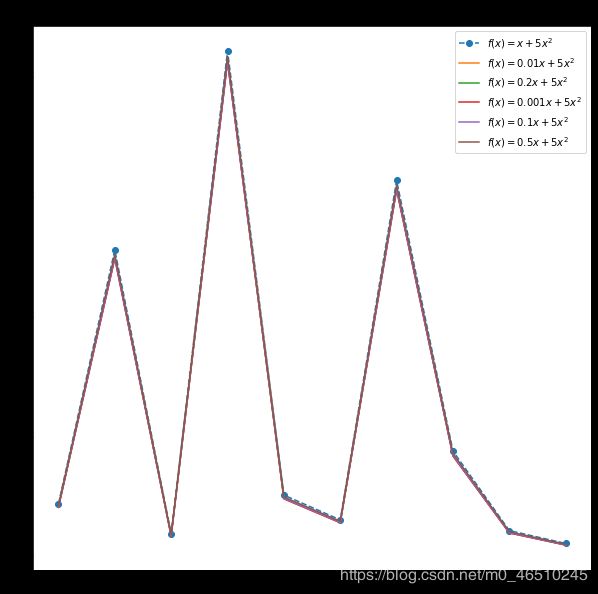
考虑以下函数-

在上面的函数中，我们在RHS上有两个术语：x和x²。 系数分别为1和5。 在下图中，我们可以看到，当第一个系数被改变时，函数的行为不会发生太大变化。

以下是原始函数的不同变体中的系数，可以称为非有效系数。 舍弃这些系数并不会真正改变函数的行为。

扩展到神经网络

以上概念也可以应用于神经网络。 这需要更多细节才能展开，需要考虑训练好的网络的权重。 我们如何理解不重要的权重？ 这里的前提是什么？

请考虑使用梯度下降的优化过程。 并非所有权重都使用相同的梯度幅度进行更新。 给定损失函数的梯度是相对于权重（和偏差）而言的。 在优化过程中，某些权重将使用比其他权重更大的梯度幅度（正负）进行更新。 优化器认为这些权重很重要，可以最大程度地减少训练目标。 接受相对较小梯度的权重可以认为是不重要的。

训练完成后，我们可以逐层检查网络的权重并找出重要的权重。 可以使用多种启发式方法做出此决定-

• 我们可以以降序的方式对权重进行排序，并选择队列中较早出现的权重。 这通常与我们想要达到的稀疏程度（要修剪的权重百分比）结合在一起。
• 我们可以指定一个阈值，并且所有大小超过该阈值的权重都将被认为是重要的。 该方案可以具有以下几种分类：

i. 阈值可以是整个网络内部最低的权重值。

ii. 该阈值可以是网络内部各层本身的权重值。 在这种情况下，重要的权重会逐层过滤掉。

如果有些难以理解，请不要担心。 在下一节中，这些将变得更加清晰。

修剪训练好的神经网络

现在，我们对所谓的重要权重有了相当的了解，我们可以讨论基于幅度的修剪。 在基于幅度的修剪中，我们将权重大小视为修剪的标准。 通过修剪，我们真正的意思是将不重要的权重归零。 遵循以下代码和摘要可能有助于理解这一点-

# Copy the kernel weights and get ranked indices of the
# column-wise L2 Norms
kernel_weights = np.copy(k_weights)
ind = np.argsort(np.linalg.norm(kernel_weights, axis=0))
    
# Number of indices to be set to 0
sparsity_percentage = 0.7
cutoff = int(len(ind)*sparsity_percentage)

# The indices in the 2D kernel weight matrix to be set to 0
sparse_cutoff_inds = ind[0:cutoff]
kernel_weights[:,sparse_cutoff_inds] = 0.

这是权重学习后将发生的变换的图形表示-

它也可以应用于偏差。 要注意这里我们考虑的是接收形状（1,2）且包含3个神经元的输入的整个层。 通常建议在修剪网络后对其进行重新训练，以补偿其性能的下降。 进行此类重新训练时，必须注意，修剪后的权重不会在重新训练期间进行更新。

实际情况

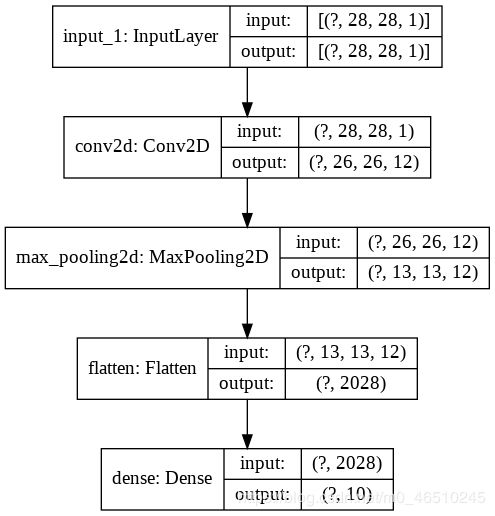
为简单起见，我们将在MNIST数据集上测试这些概念，但您也应该能够将其扩展到更复杂的数据集。 我们将使用具有以下拓扑结构的浅层全连接网络-

该网络共有20,410个可训练参数。 对该网络进行10个时期的培训可以为我们奠定良好的基础-

现在开始修剪吧！ 我们将使用tensorflow_model_optimization（别名为tfmot）。 tfmot为我们提供了两种修剪方法：

• 采取训练好的网络，并通过更多次数的培训来修剪它。
• 随机初始化网络，并从头开始进行修剪训练。

我们将对它们两个进行试验。 这两个都应包括修剪网络，我们将在稍后讨论。 以训练形式修剪网络的基本原理是更好地指导训练过程，以便可以相应地进行梯度更新，以有效地调整未修剪的权重。

请注意，还可以修剪模型中的特定图层，而tfmot确实允许您这样做。 查看https://www.tensorflow.org/model_optimization/guide/pruning/comprehensive_guide 以了解更多信息。

方法1：对训练好的网络，网络接受更多训练后修剪它

从现在开始，鼓励您遵循上面提到的Colab笔记本。

我们将采用我们之前训练的网络并从那里修剪它。 我们将应用修剪计划，以在整个训练过程中保持稀疏程度不变（由开发人员指定）。 具体代码如下：

pruning_schedule = tfmot.sparsity.keras.ConstantSparsity(
          target_sparsity=target_sparsity,
          begin_step=begin_step,
          end_step=end_step,
          frequency=frequency
)

pruned_model = tfmot.sparsity.keras.prune_low_magnitude(
    trained_model, pruning_schedule=pruning_schedule
)

修剪的模型需要重新编译，然后才能开始对其进行训练。 我们以相同的方式对其进行编译，并打印其摘要-

pruned_model.compile(loss='sparse_categorical_crossentropy',
    optimizer='adam',
    metrics=['accuracy'])

pruned_model.summary()

网络结构如下

Layer (type)                 Output Shape              Param #   
=================================================================
prune_low_magnitude_conv2d ( (None, 26, 26, 12)        230       
_________________________________________________________________
prune_low_magnitude_max_pool (None, 13, 13, 12)        1         
_________________________________________________________________
prune_low_magnitude_flatten  (None, 2028)              1         
_________________________________________________________________
prune_low_magnitude_dense (P (None, 10)                40572     
=================================================================
Total params: 40,804
Trainable params: 20,410
Non-trainable params: 20,394
_________________________________________________________________

我们看到参数的数量现在已经改变。 这是因为tfmot为网络中的每个权重添加了不可训练的掩码，以表示是否应修剪给定的权重。 掩码为0或1。

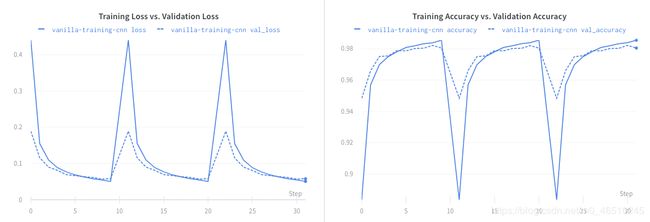
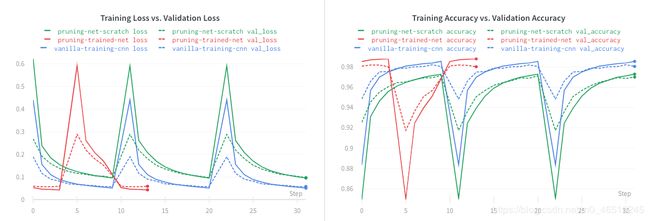
让我们训练这个网络。

我们可以看到修剪模型不会损害性能。 红线对应于修剪后的实验。

注意：

• 必须指定修剪计划，以便在训练模型时实际修剪模型。 我们还指定UpdatePruningStep回调，以使其在训练过程中处理修剪更新。
• PruningSummaries提供有关在训练期间如何保持稀疏度和幅度阈值的摘要。
• 将修剪计划视为超参数。 tfmot提供了另一个现成的修剪计划-PolynomialDecay。
• 将修剪计划中的end_step参数设置为小于或等于训练模型的时期数。 另外，您可能需要试验一下frequency（表示应应用修剪的频率），以便获得良好的性能以及所需的稀疏性。

我们还可以通过编写如下测试来验证tfmot是否达到了目标稀疏性：

for layer in model.layers:
	if isinstance(layer, pruning_wrapper.PruneLowMagnitude):
	    for weight in layer.layer.get_prunable_weights():
	        print(np.allclose(
	            target_sparsity, get_sparsity(tf.keras.backend.get_value(weight)), 
	            rtol=1e-6, atol=1e-6)
            )

def get_sparsity(weights):
    return 1.0 - np.count_nonzero(weights) / float(weights.size)

在修剪的模型上运行它应该为修剪的所有层生成True。

方法2：随机初始化网络，通过从头开始训练来修剪网络

在这种情况下，除了我们不是从一个已经训练的网络开始，而是从一个随机初始化的网络开始，一切都保持不变。

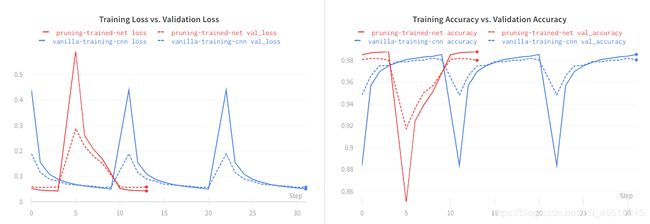
绿线对应于从头开始实验的修剪。 我们可以观察到相对于其他两个模型，性能有所下降，但这是可以预料的，因为我们不是从一个已经训练好的模型开始的。

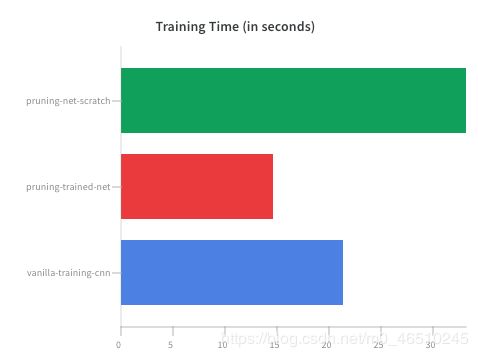
当我们通过从头开始训练来修剪网络时，通常会花费最多的时间。 由于网络正在研究如何最好地更新参数以达到目标稀疏度，这也是可以预料的。

要真正理解修剪的力量，我们需要更深入地研究：

• 导出同一网络的已修剪和未修剪的类型，对其进行压缩，然后记下其大小。
• 量化它们，压缩它们的量化版本，记下它们的大小，并评估它们的性能。

让我们在下一部分中进行处理。

评估

我们将使用标准的zipfile库将模型压缩为.zip格式。 序列化修剪的模型时，我们需要使用tfmot.sparsity.keras.strip_pruning，它将删除tfmot添加到模型的修剪包装。 否则，我们将无法在修剪的模型中看到任何压缩优势。

但是，压缩后的常规Keras模型仍然相同。

    with zipfile.ZipFile(zipped_file, 'w', compression=zipfile.ZIP_DEFLATED) as f:
        f.write(file)

    return os.path.getsize(zipped_file)

file应该是已经序列化的Keras模型的路径（修剪和常规）。

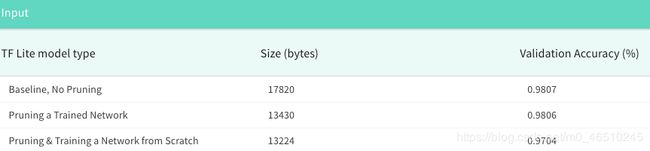
在下图中，我们可以看到压缩模型的大小小于常规Keras模型，并且它们仍具有相当好的性能。

我们可以使用TensorFlow Lite量化模型以进一步在不影响性能的前提下减小模型尺寸。 请注意，在将修剪后的模型传递给TensorFlow Lite的转换器时，您应该去除修剪后的包装。

除精度测量外，压缩率是另一种广泛使用的用于测量特定修剪算法的指标。 压缩率是修剪后的网络中剩余参数的分数的倒数。

这种量化的方式也称为训练后量化。 因此，这里有一个简单的方法供您遵循，以优化您的部署模型：

在下一节中，我们将介绍一些现代修剪方法。 如果您想进一步追求模型优化，那么这些想法将值得进一步探索。

一些现代修剪方法

让我们从以下问题开始本节：

1. 当我们重新训练修剪后的网络时，如果未修剪的权重初始化为它们的原始参数大小会怎样？ 如果您是从经过训练的网络（例如网络A）中获得的修剪的网络，请考虑网络A的这些初始参数的大小。
2. 当在具有预训练网络的迁移学习方案中执行基于量级的修剪时，我们如何确定权重的重要性？

中奖的彩票

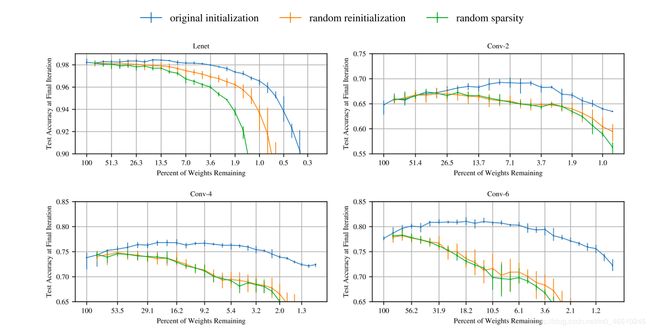
Frankle等人在他们关于彩票假说的开创性论文(https://arxiv.org/abs/1803.03635)中对第一个问题进行了极大的探索。 因此，在修剪已经训练好的网络之后，将具有上述刚刚初始化的子网络称为Of Winning Tickets。

资料来源：原论文

根据此方法的基本原理，您可以推断出，在网络的初始训练期间，参数的特定初始化方式指导了优化过程。 现在，在优化环境中响应良好的权重（意味着它们比其他权重传播得更远）实际上最终落入了中奖彩票。 因此，为了使它很好地进行（重新）训练，我们将权重初始化为最大，这样优化过程会很好地吸引他们。

本文提出了许多不同的实验来支持这一假设，因此绝对推荐阅读。

彩票假说的系统探索

在原始的彩票假说论文中，Frankle等人。 仅探讨了如果在训练之前将权重重新初始化为最大初始大小，则修剪后的网络的性能如何。 在ICLR 2019上提出彩票假说后，Zhou等 发表了一篇关于“解构彩票”的论文(https://arxiv.org/abs/1905.01067)，研究了在修剪过程中处理存活下来和未存活下来的权重的不同方法。 还提出了超级掩模。

资料来源：原论文

彩票假说的推广

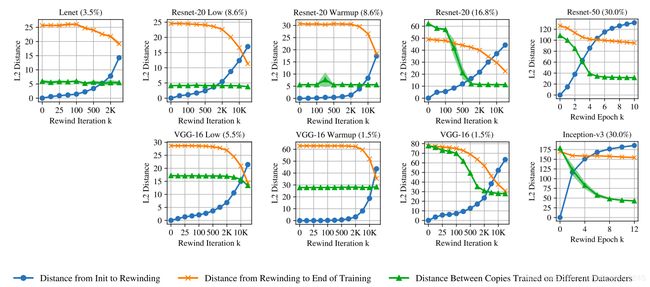
为了能够将彩票假说使用到ImageNet，Frankle等人的数据集，有人发表了关于线性模式连通性的论文(https://arxiv.org/abs/1912.05671)，该论文对彩票假设进行了概括。 它提出了权重反卷积后作为修剪后初始化网络权重的一种潜在方法。 之前，我们以最大的初始量来初始化它们。 权重反卷积的作用是将剩余的权重倒带到原始网络训练中的某个位置。 换句话说，幸存的权重从原始网络训练的批次5开始初始化。

资料来源：原论文

Renda等人扩展了这个想法。 发表了一篇有关“学习速率倒带”的论文，该论文适用于在训练经过修剪的网络时倒带学习率时间表。 作者还建议将其作为微调的替代方法。

这是一些令人兴奋的想法，主要围绕基于幅度的修剪而发展。 在最后一节中，我们将看到一种比基于幅度的修剪效果更好的修剪方法，尤其是对于迁移学习机制而言。

根据权重变化进行修剪

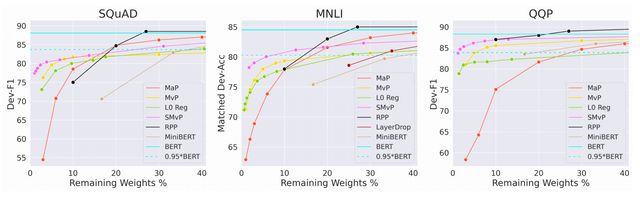
Sanh等人在有关权重变化修整的论文(https://arxiv.org/abs/2005.07683)中。 提出了一种基于幅度的修剪的替代方法，该方法专门用于处理用于迁移学习任务的预训练模型的修剪。

基于幅度的修剪与我们之前已经讨论过的重要性概念正相关。 在这种情况下，此处的重要性仅表示权重的绝对大小。 这些幅度越低，意义就越小。 现在，当我们尝试使用在不同数据集上预先训练的模型进行迁移学习时，这种重要性实际上可以改变。 优化源数据集时重要的权重可能对目标数据集不重要。

资料来源：原论文

因此，在迁移学习期间，朝着零移动的预训练权重相对于目标任务实际上可以被认为是不重要的，而向远处移动的权重可以被认为是重要的。 这就是该方法的运动修剪。

结论和最终想法

我希望这份报告能使您对深度学习背景下的修剪有一个清晰的认识。 我要感谢Raziel和Yunlu（来自Google），向我提供了有关tfmot的重要信息以及有关修剪自身的其他一些想法。

我想在此领域中探索的其他一些想法是：

• 如果我们可以在训练和再训练带有修剪功能的网络时使用区分性的修剪时间表，该怎么办？
• 当进行幅度修剪时，Zhou等人。 向我们展示了在修剪的网络中处理权重初始化的不同方法。 我们可以学习一种有效的方法来系统地结合它们吗？

在撰写本报告时（2020年6月），修剪的最新方法之一是SynFlow。 SynFlow不需要任何数据来修剪网络，它使用Synaptic Saliency Score来确定网络中参数的重要性。

我很乐意通过Twitter（@RisingSayak）听到您的反馈。

引用（无特定顺序）

• Model Pruning Exploration in Keras by Matthew Mcateer
• Official tfmot guide on Pruning in Keras
• Dissecting Pruned Neural Networks by Frankle et al.
• Lottery Ticket Hypothesis explanation video by Yannic Kilcher
• Movement Pruning explanation video by Yannic Kilcher

作者：Sayak Paul

deephub翻译组：孟翔杰