在算法江湖中一直流傳著單純形法的各式傳說,George Dantzig 做課後作業搞出的單純形法啦,單純形法就是在高維凸面體的頂點間遊走啦,單純形法是高斯消元法的變形啦(這貨哪像高斯消元法了?!)……
也許,單純形法的晦澀源於它處理的是高維空間。下面,我們從實例出發,看看能否參悟這隱藏在代數中的幾何直觀吧。
我們先來看看這個問題:
max 2x + y
s.t. x + y ≤ 5
2x + 3y ≤ 12
x ≤ 4
and x, y ≥ 0
一切都是從妄想開始的。我們要讓z = 2x + y儘可能地大。注意到x, y ≥ 0,而z - 2x - y = 0。要是x和y前的係數是正的就好了,比如z + 2x + 3y = 17,那我們立馬可以得出z_max = 17。因為z要儘可能大,那x、y就得儘可能小,當它們縮至零時,z取得最大值。那怎麼才能約束變元的係數“轉正”呢?
現在,我們先放一放“轉正”的事,考慮一下如何把不等式變為等式。其實很簡單,補足。2x + 3y不是小於或等於12嘛,那就加上一個大於或等於零的變元,即2x + 3y + v = 12, v ≥ 0。這樣一來,問題就變成了半個線性代數問題了:
z - 2x - y = 0
x + y + u = 5
2x + 3y + v = 12
x + w = 4
and x, y, u, v, w ≥ 0
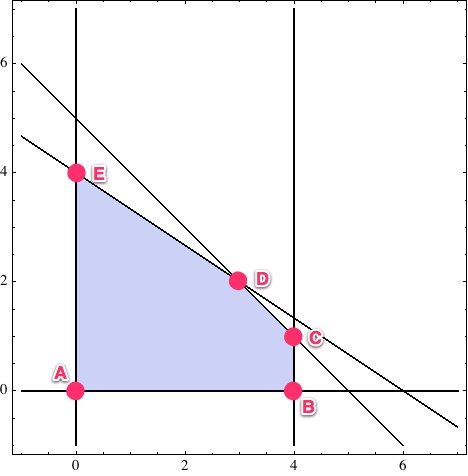
話說無端給你多整出三變元來,不是“酒入愁腸愁更愁”嘛。在此按住不表,我們先來看看那五條約束圍成的區域:
x + y ≤ 5
2x + 3y ≤ 12
x ≤ 4
x ≥ 0
y ≥ 0
現在我們把方程組變換個形式:
y + u + x = 5
y - 2u + v = 2
-y - u + w = -1
and x, y, u, v, w ≥ 0
上面這組方程等價于下面這組約束:
y + u ≤ 5
y - 2u ≤ 2
-y - u ≤ -1
y ≥ 0
u ≥ 0
畫出圖來就是:
你看出门道了吗?还没有,那我们继续变换:
(什麼時候我才能把這篇給寫完啊!!!)
require 'pp'
require 'set'
DEBUG = false
class String
def to_terms() self.gsub("-", "+-").split(/\\s*\\+/).select{|e| e != ""} end
def to_pair
r = /
( (\\-)? (\\d+(\\.\\d+)?)? ) # e.g. -3.2, 4, -
\\*?
(\\w+ (\\d+)?) # e.g. x2
/x
if r =~ self.gsub(/\\s+/, "")
c = $3.nil? ? 1 : $3.to_f
c = -c if not $2.nil?
return $5.to_sym, c
else
p "err!"
end
end
end
class Array
def scalar_mult!(c) self.map! {|e| e*c} end
def scalar_mult(c) self.map {|e| e*c} end
def vector_add!(v) self.each_with_index {|_, i| self[i] += v[i]} end
end
class Hash
def dot_prod
e = []
self.each do |k, v|
if v != 0
if v == 1
e << k.to_s
elsif v == -1
e << ("-" + k.to_s)
else
e << (v.to_s + k.to_s)
end
end
end
e.join(' + ').gsub("+ -", "- ")
end
end
class Simplex
def initialize(path)
m = /
(max|Maximize) \\s+ (.+?) \\n
\\s* (s\\.t\\.|subject \\s+ to) \\s+ (.+?)\\.
/mx
if m =~ File.read(path)
@z_equ = {:b => 0} # objective equation
$2.to_terms.each do |term|
k, v = term.to_pair
@z_equ[k] = -v
end
@nonbasic_vars = []
@basic_vars = []
@matrix = []
idx = 1
$4.split(/[\\n,]/).each do |inequalities|
if / (\\w+(\\d+)?) \\s* >= \\s* 0 /x =~ inequalities # xi >= 0
@nonbasic_vars << $1.to_sym
elsif / \\s* (.+?) \\s* <= \\s* (\\d+(\\.\\d+)?) /x =~ inequalities
lhs, rhs = $1.to_s, $2.to_f
equ = {:b => rhs, :"$#{idx}" => 1}
@basic_vars << :"$#{idx}"
idx += 1
lhs.to_terms.each do |t|
k, v = t.to_pair
equ[k] = v
end
@matrix << equ
else
p "err!"
end
end
else
p "err!"
end
end
def canonical_form
@vars = @nonbasic_vars + @basic_vars
@mtr = [[]] # coefficient matrix
@vars.each_with_index do |x, k|
@mtr[0][k] = @z_equ[x] || 0
end
@mtr[0] << @z_equ[:b]
@matrix.each_with_index do |row, i|
ary = []
@vars.each_with_index do |x, j|
ary[j] = row[x] || 0
end
ary << row[:b]
@mtr << ary
end
puts "max " + @z_equ.dot_prod
print "s.t.\\n"
@matrix.each {|r| print "#{r.select{|k, v| k!=:b}.dot_prod} = #{r[:b]}\\n"}
print "and " + @vars.join(" >= 0, ") + " >= 0.\\n"
end
def mtr_display()
@mtr.each do |r|
puts Hash[*@vars.zip(r).flatten].dot_prod + " = #{r[-1]}"
end
end
def solve
DEBUG && puts("---------------------------------------------------------------")
DEBUG && mtr_display
pivot_c = @mtr[0].min
pivot_var = @mtr[0].index pivot_c
if pivot_c >= 0
@z_max = @mtr[0][-1]
else
n = @mtr.size - 1
idx = 1
_a = @mtr[1][pivot_var]
_b = @mtr[1][-1]
(1..n).each do |i|
idx = i if _a * @mtr[i][-1] < _b * @mtr[i][pivot_var]
end
v_i = @vars.index :"$#{idx}"
c = 1.0/@mtr[idx][pivot_var]
@mtr[idx].scalar_mult! c
@mtr.each_with_index do |row, i|
if i != idx
row.vector_add!(@mtr[idx].scalar_mult(-@mtr[i][pivot_var]))
end
end
DEBUG && puts(" ...(#{@vars[v_i]} -> #{@vars[pivot_var]})...")
DEBUG && mtr_display
self.solve
end
@z_max
end
end
s = Simplex.new("./simplex.data")
s.canonical_form
puts "\\nf(z)_max = #{s.solve}"
simplex.data:
max 2x1 + x2
s.t. x1 <= 4
2x1 + 3x2 <= 12
x1 + x2 <= 5
x1 >= 0, x2 >= 0.
輸出:
max -2.0x1 - x2
s.t.
$1 + x1 = 4.0
$2 + 2.0x1 + 3.0x2 = 12.0
$3 + x1 + x2 = 5.0
and x1 >= 0, x2 >= 0, $1 >= 0, $2 >= 0, $3 >= 0.
f(z)_max = 9.0