【动态规划】最小编辑距离（字符串A到字符串B变化最少要多少步）

最小编辑距离是一道非常经典的动态规划问题。

设A 和B 是2 个字符串。要用最少的字符操作将字符串A 转换为字符串B。 
这里所说的字符操作包括 
(1)删除一个字符； 
(2)插入一个字符； 
(3)将一个字符改为另一个字符。 
将字符串A变换为字符串B 所用的最少字符操作次数也称为字符串A到B 的编辑距离，记为 d(A,B)。 
试设计一个有效算法，对任给的2 个字符串A和B，计算出它们的编辑距离d(A,B)。 

为什么要把这个问题又搬出来呢？因为我发现，网络上有好多错误代码，错误思路，这种错误代码，流传甚广，被多个博客学习又再次推广发表。我觉得应该纠正一下了。

先说一下错误的版本。以下位置坐标皆从0开始计数。

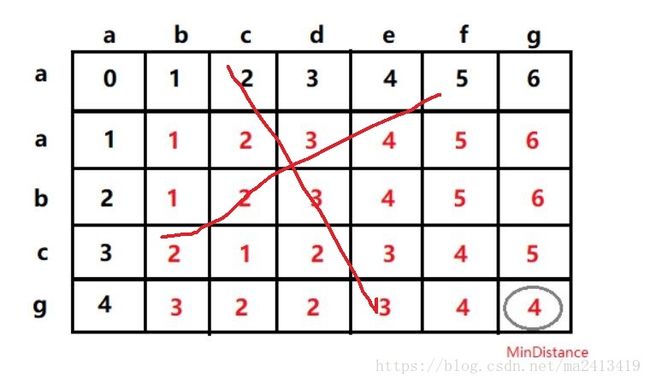
凡是用到这张图的，全是错误的！

为什么这么说呢？我讲下每一个单元格的数字代表的意义。如上图所示，比如（0,6）位置的数字6 代表字符串“abcdrfg”变为字符串“a”需要的最少步数为6，再比如（1,1,）位置处的数字1代表字符串“ab”变为字符串“aa”需要的最少步数为1。

乍一看，这张图也没问题啊，然而这种写法是错误的，这张图成立只基于两个字符串的首字母相同的情况。配有这张图的大部分博客中的代码都是错误的。比如“a”和“b”，也会检测为需要0步。

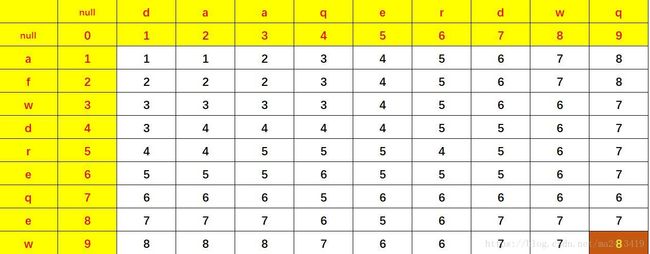
真正的图为：

该图中示例为字符串“daaqerdwq”转化为字符串“aswdreqew”。

此时我们可以看到位于（2,2）位置的数字1，对应的是字符串“d”转化为字符串“a”互相转化需要的最少步数。最右下角的褐色区域的数字8，代表字符串“daaqerdwq”转化为字符串“aswdreqew”需要的最小步数。

这个思路是怎么来的呢？首先假设两个字符串都为空，则需要0步就可转化。所以表格最左上角要写0，然后字符串A加入一个字符‘d’，此时需要1步才能做到转化，同理，若是B为空字符串，A字符串有几个字符，就要做几步删除操作。

若是字符串B中有一个字符，如上图中的“a”，重复A字符串从“ ”到“daaqerdwq”不断加入字符的过程，即可得出如下规律

 D[i][j]=min(min(D[i-1][j]+1,D[i][j-1]+1),(A[j-1]==B[i-1]?D[i-1][j-1]:D[i-1][j-1]+1));

D[i][j]是指上图中数字区域的每个单元格的值。

完整代码如下：

#include
#include

using namespace std;

int MinEditDistance(string A,string B)
{
    int len_A = A.length();
    int len_B = B.length();
    int D[len_B+1][len_A+1];
    D[0][0]=0;
    for(int i=1;i<=len_A;i++)
    {
        D[0][i]=i;
    }
    for(int i=1;i<=len_B;i++)
    {
        D[i][0]=i;
    }
    for(int i=1;i<=len_B;i++)
    {
        for(int j=1;j<=len_A;j++)
            D[i][j]=min(min(D[i-1][j]+1,D[i][j-1]+1),(A[j-1]==B[i-1]?D[i-1][j-1]:D[i-1][j-1]+1));
    }
    return D[len_B][len_A];

}

int main()
{
    string A,B;
    cin>>A>>B;
    cout<

虽说天下博客一般抄，但大家还是不要去借鉴错误的博客了。